شبکه عصبی چیست؟ (بخش دوم)

در جلسه سوم آموزش شبکه عصبی هم مشابه قسمت دوم می خواهیم در مورد شبکه عصبی صحبت کنیم و موضوعات مختلفی را مورد بررسی قرار دهیم تا دید وسیع تری نسبت به آن پیدا کنید و برای یادگیری جلسات بعدی آماده شوید.

چرا جمع وزنی داریم؟

در جلسه قبل آموزش شبکه عصبی در سایت دیتایاد دیدیم که درون نورونی با تعدادی ویژگی های ورودی و تعدادی خروجی، محاسباتی انجام می شود. به این محاسبات، جمع وزنی می گوییم. همچنین دیدیم که به ازای هر ویژگی ورودی، ماتریس وزن ها یک مولفه جداگانه دارد.

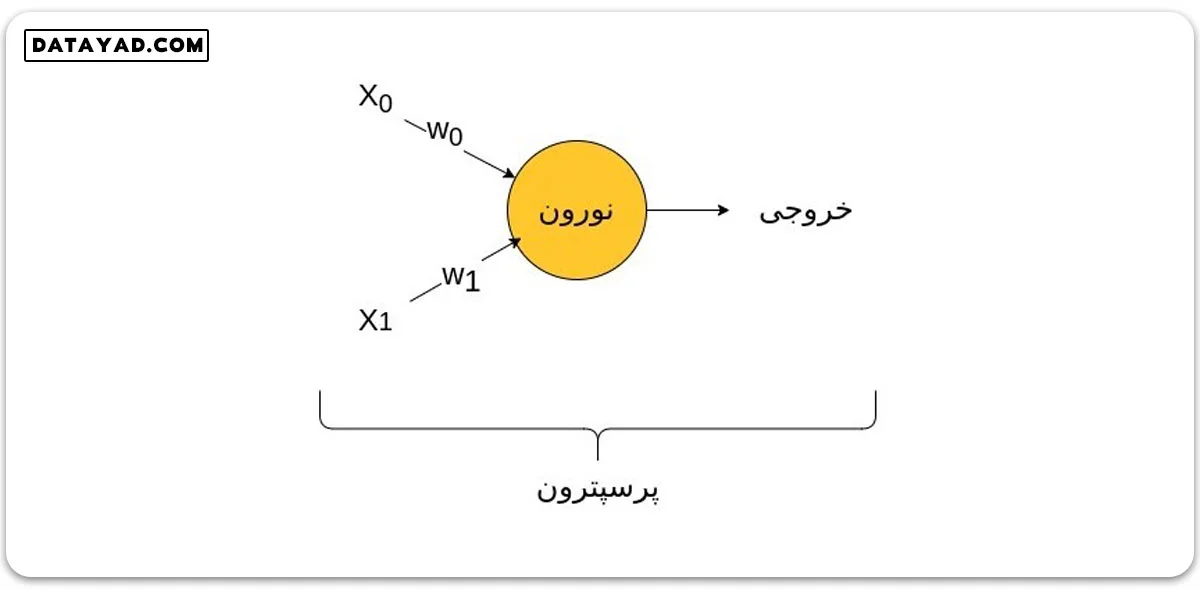
به واحد پردازشی که محاسبات را انجام می دهد نورون، و به کلیت تصویر زیر پرسپترون می گوییم که البته این تصویر ناقص در انتهای همین جلسه تکمیل خواهد شد.

بررسی دقیق تر محاسبات در شبکه عصبی

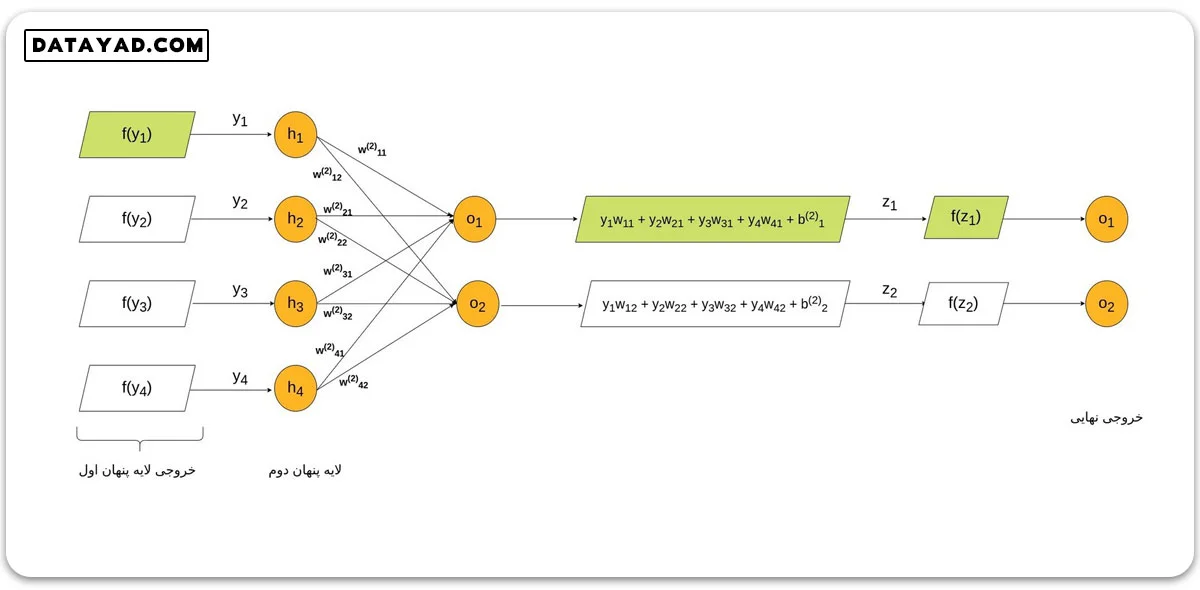
در تصویر زیر جزئیات محاسبات در شبکه عصبی به طور دقیق نشان داده شده است. در این تصویر سه ورودی داریم. همچنین مشاهده می کنیم که به ازای هر پیکان که از ورودی ها به سمت نورون های لایه پنهان می رود، یک مولفه وزن وجود دارد. در این تصویر، محاسباتی که در هر یک از نورون های لایه پنهان انجام می شود، مقابل نورون مربوطه قابل مشاهده است.

به عنوان مثال به نورون اول در لایه پنهان، سه مقدار w₂₁ ،w₁₁ و w₃₁ وارد می شود. به همین ترتیب به ازای هر نورون لایه اول، وزن هایی به تمام نورون های لایه دوم ارسال می شود. بنابراین در هر نورون لایه دوم، یک جمع وزنی صورت می گیرد.

دقت کنید که در مورد هر کدام از این جمع های وزنی، ایندکس اول هر کدام از مولفه های w با شمارنده x یا ورودی مربوطه و ایندکس دوم آن با شمارنده y و یا خروجی مربوطه یکسان است. در حالات کلی ضرب ماتریسی انجام شده در شبکه تک لایه ای بالا برابر است با:

از آنجایی که لایه پنهان شکل فوق چهار خروجی دارد، ماتریس بایاس یک ماتریس چهار مولفه ای است که هر مولفه با حاصل جمع وزنی نورون متناظر این لایه جمع می شود.

توجه کنید همان طور که در شکل نشان داده شده است، خروجی هر نورون لایه پنهان، به عنوان ورودی یک تابع لحاظ شده که همان تابع فعالسازی است. در خصوص این تابع در ادامه صحبت خواهیم کرد. خروجی این تابع به لایه بعد خواهد رفت که این لایه می تواند لایه پنهان بعدی و یا لایه خروجی نهایی باشد.

نحوه انتقال مقادیر در لایه های شبکه عصبی

فرض کنید ادامه شبکه فوق به شکل زیر باشد. در این صورت خروجی لایه پنهان اول به لایه پنهان دوم رفته و در نهایت خروجی این لایه به عنوان خروجی نهایی شبکه عصبی در نظر گرفته می شود. در این حالت وزن های جدیدی در مقادیر نورون های لایه دوم ضرب شده و پس از عبور از تابع فعالسازی، خروجی لایه پنهان دوم را می سازند.

در ساده ترین حالت،‌ مقداردهی اولیه ماتریس وزن ها و بایاس در کل شبکه به صورت تصادفی انجام می شود. سپس با محاسبه تابع زیان (loss function) و طی الگوریتم پس انتشار (back propagation) این مقادیر آپدیت می شوند. روند این محاسبات را در جلسات آینده دقیق تر بررسی خواهیم کرد.

بررسی دقیق تر ویژگی های بایاس در شبکه های عصبی

همان طور که در بحث مربوط به رگرسیون خطی گفتیم، بایاس را می توان به عنوان عرض از مبدأ در نظر گرفت. ویژگی دیگر بایاس اینست که تا حدودی از سوگیری مدل جلوگیری می کند. نامگذاری بایاس هم به همین علت بوده است.

برای روشن تر شدن این موضوع فرض کنید ورودی های ما یعنی x_i ها روی تعدادی از نورون ها صفر باشند. در این صورت مستقل از مقدار وزن، حاصل جمع وزنی صفر می شود و ورودی مربوطه تاثیر خود را در شبکه از دست می دهد.

یکی از کارکردهای بایاس اینست که در چنین مواقعی با صفر جمع شده و یک مقدار تأثیرگذار در شبکه ایجاد کند و بدین ترتیب جلوی بی اثر بودن ورودی صفر در شبکه را بگیرد.

بدین ترتیب تا اینجا با مقدمات شبکه عصبی آشنا شدیم. نکته ای که باید در نظر داشته باشیم اینست که توجیه رفتار لایه های میانی خیلی امکان پذیر نیست. به همین دلیل به مدل شبکه عصبی اصطلاحا جعبه سیاه (black box) می گویند. این موضوع سبب می شود مدل های بزرگ گاهی رفتاری نشان دهند که پیش از آموزش شبکه، قابل پیش بینی نبوده است.

هدف ما این است که بینشی کلی از نحوه آموزش و بهینه شدن مدل داشته باشیم تا بدانیم اگر جایی انفجار گرادیان یا محو شدگی گرادیان یا رویداد غیرقابل انتظار دیگری روی داد، چطور پارامترها را تغییر دهیم تا مدل به درستی آموزش ببیند. به طور کلی هدف ما اینست که رفتار شبکه و الگوریتم را بشناسیم تا بتوانیم پارامترها را به درستی تنظیم کنیم.

درباره این موارد در جلسات آینده بررسی مفصل تری خواهیم داشت. 

مفهوم اولیه تابع فعالسازی (activation function)

همان طور که دیدیم خروجی هر نورون یک جمع وزنی به صورت زیر است:

Z=X×W+B

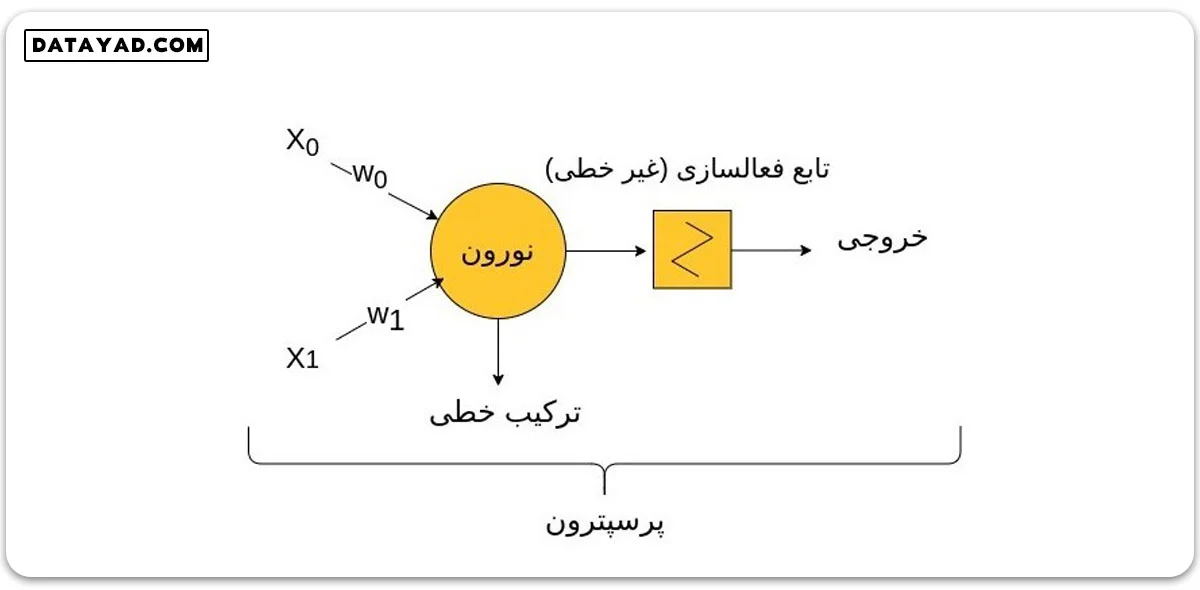
این جمع وزنی، ورودی تابع فعالسازی است. تابع فعالسازی یکی از هایپر پارامترهایی است که می توانیم در مدل تغییر دهیم. کارکرد اصلی این تابع اینست که رفتار غیر خطی را به مدل اعمال می کند تا بتوان مدل های پیچیده تری برای مسائل پیچیده تر ایجاد کرد.

بدون اعمال یک تابع غیرخطی، افزایش تعداد لایه های پنهان، تاثیر کمتری در پیچیده کردن مدل خواهد داشت و همچنین درک پیچیدگی داده ها توسط مدل کاهش پیدا می‌کند.

با وارد کردن تابع فعالسازی، تصویر پرسپترون ابتدای این درس تکمیل شده و به شکل نهایی زیر می رسد:

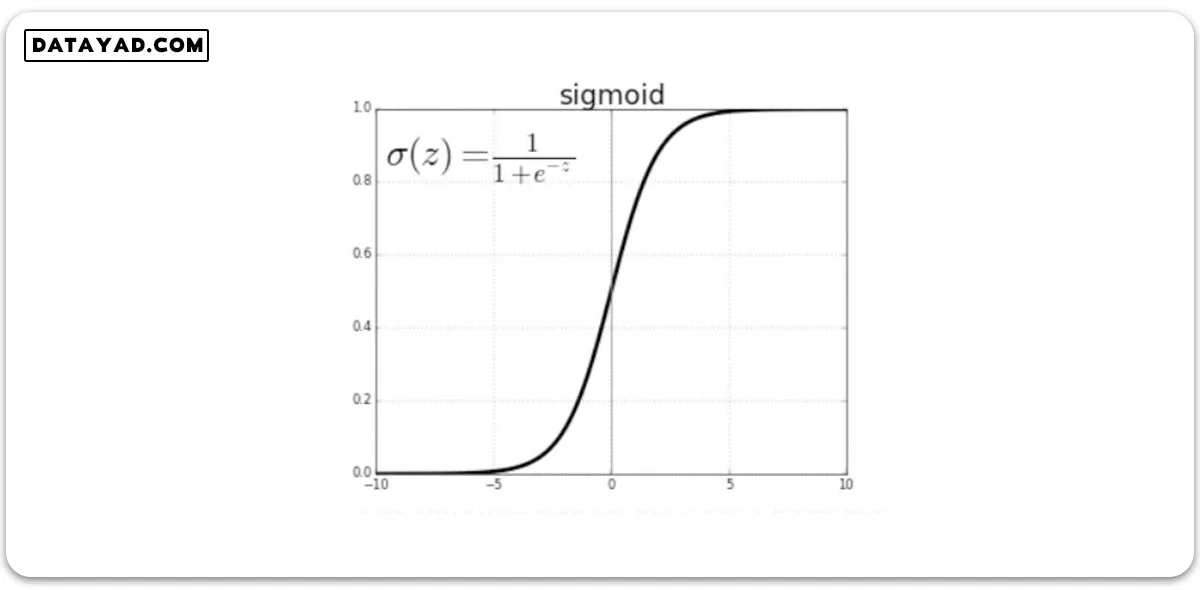
علاوه بر این توابع فعالسازی مزایای دیگری هم دارند. مثلا تابع فعالسازی سیگموید که در شکل زیر نشان داده شده است، خروجی را بین صفر و یک نرمال می کند که این مسأله اهمیت زیادی دارد. زیرا شبکه ما در لایه های مختلفی آموزش می بیند و ممکن است در قسمت هایی از شبکه، خروجی خیلی بزرگ یا خیلی کوچک شود.

این امر باعث می شود یک سری از ویژگی ها خیلی زیاد دیده شوند و یا اصلا دیده نشوند. نرمال سازی خروجی از به وجود آمدن این حالت ها جلوگیری می کند. در آینده بیشتر به مفهوم توابع فعالسازی در سایت دیتایاد خواهیم پرداخت.