در جلسه ششم از آموزش رایگان شبکه عصبی می خواهیم به توابع فعالسازی (activation function) در شبکه عصبی بپردازیم. با ما همراه باشید.
بررسی دقیق تر توابع فعالساز
انواع توابع فعالساز و کاربردهای این توابع
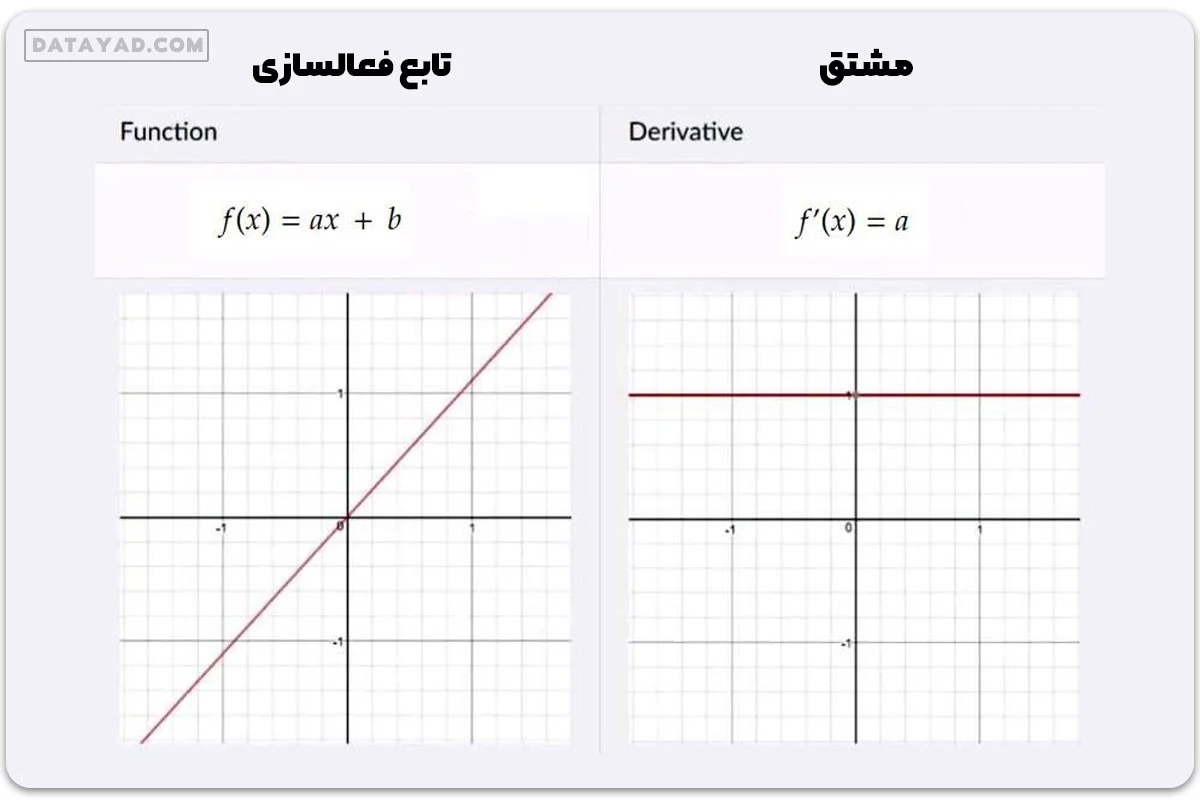
۱- تابع فعالسازی خطی
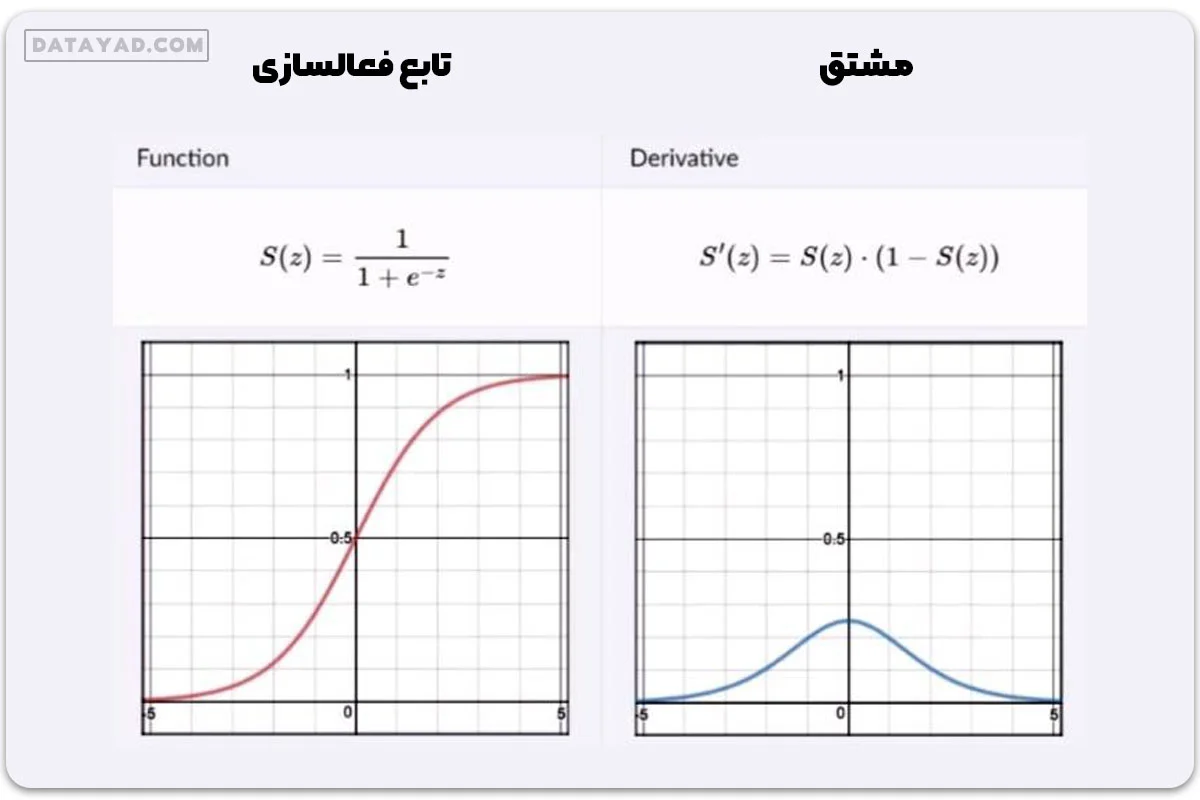
۲- تابع فعالسازی سیگموید
- در نقطه x=0 مقدار این تابع برابر 0.5 است.
- مقدار این تابع همواره بین 0 و 1 است.
- به ازای مقادیر خیلی کوچک و خیلی بزرگ x، مقدار تابع به ترتیب به 0 و 1 میل می کند.
- مشتق این تابع به ازای مقادیر خیلی کوچک و خیلی بزرگ x، به 0 میل می کند. این می تواند موجب ایجاد محوشدگی گرادیان شود که در ادامه به آن خواهیم پرداخت.
محدود بودن این تابع بین صفر و یک باعث می شود بتوان از خروجی این تابع تعبیر احتمالی داشت. مثلا اگر مسأله ما دسته بندی تصاویر به دو کلاس سگ و گربه باشد، می توانیم به هر کدام از کلاس ها مانند زیر، یک عدد نسبت دهیم:
سپس خروجی مدل را از تابع فعالسازی سیگموید عبور می دهیم تا در نهایت عددی بین صفر و یک به عنوان خروجی نهایی مدل داشته باشیم. در این صورت می توانیم این خروجی را به این شکل به صورت احتمالی تفسیر کنیم:
البته انتخاب 0.5 به عنوان آستانه اختیاری است. نکته مهم این است که در این حالت هر چه عدد خروجی به 1 نزدیک تر باشد، احتمال گربه بودن ببیشتر است و کمتر شدن عدد خروجی، به این معناست که مدل احتمال بیشتری می دهد که تصویر مربوطه تصویر یک سگ باشد.
در نتیجه با استفاده از سیگموید به عنوان تابع فعالسازی لایه خروجی مدل، می توانیم مسأله دسته بندی دو کلاسه را حل کنیم.
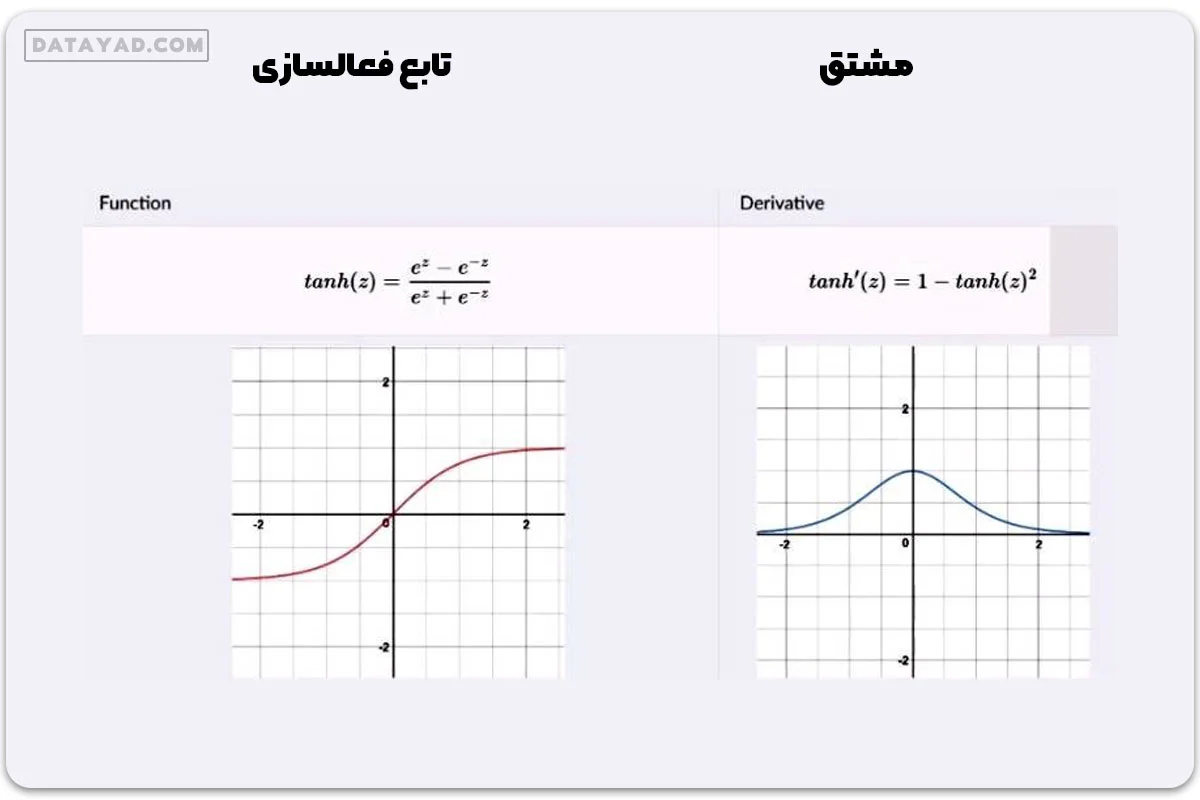
۳- تابع فعالسازی تانژانت هایپربولیک
- خروجی این تابع همواره بین -1 و 1 است.
- به ازای مقادیر خیلی کوچک و خیلی بزرگ x، مقدار تابع به ترتیب به –
محتوای دوره عالیه، ممنون از آموزش خوبتون
خداروشکر، خوشحالم که می پسندی، ممنونم که بازخورد میدی
سلام لطفا یه نرم افزار ساده برای کاربران مبتدی شبکه عصبی و رشته های غیر مهندسی هم معرفی بفرمایید
سلام
اگر از google colab استفاده کنید، نیاز به نصب ابزارها و پکیج ها ندارید و از این نظر ساده تر هست.
برای پیاده سازی شبکه های عصبی در محیط گوگل کولب، یکی از ساده ترین ابزارها keras هست.
آموزش هردوی اینها رو در یوتیوب گذاشتم،
آدرس کانال یوتیوب: https://www.youtube.com/@saberkolagar