نحوه آپدیت وزن و بایاس در شبکه عصبی

در جلسه چهارم از آموزش رایگان شبکه عصبی می خواهیم به مبحث نحوه آپدیت وزن و بایاس در شبکه عصبی بپردازیم.

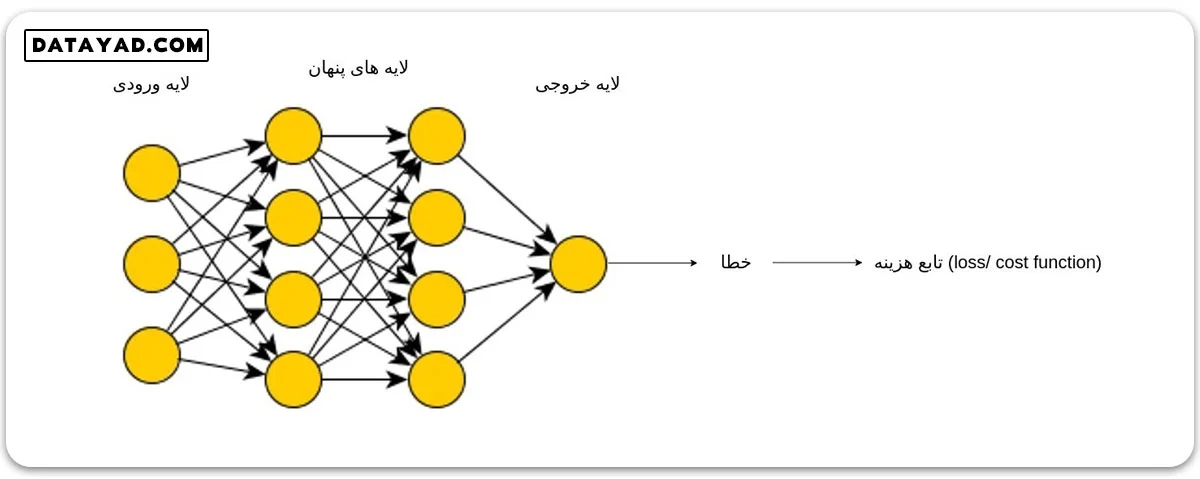
نحوه محاسبه خطا در شبکه

همان طور که گفتیم فرایند آموزش شبکه در یادگیری نظارت شده، شامل آپدیت کردن پارامترها در جهت بهینه سازی تابع هزینه است. در این بخش می خواهیم ببینیم چطور خطا را محاسبه می کنیم و نحوه آپدیت وزن و بایاس در شبکه عصبی بر اساس خطا را یاد می گیریم تا بتوانیم به حالتی با خطای بهینه برسیم.

در شبکه عصبی هم روندی مشابه همان الگوریتم بهینه سازی که پیش تر بررسی کردیم طی می شود تا وزن ها و بایاسی که در ابتدا به صورت تصادفی مقداردهی شده اند، بهینه شوند. برای این منظور، ابتدا تمامی وزن ها و بایاس ها مقداردهی اولیه می شوند. مقدار دهی اولیه وزن ها و بایاس ها معمولا به صورت رندوم انجام می‌شود.

سپس مقادیر ورودی به شبکه وارد شده و محاسبات هر لایه به ترتیب با مقادیر اولیه وزن و بایاس انجام می شود و به عنوان خروجی به لایه بعد می رود.

این روند ادامه پیدا می کند تا به لایه خروجی برسیم. در اینجا با مقایسه خروجی های تولید شده توسط شبکه عصبی با مقادیر هدف، میزان خطا محاسبه می شود.

این مقایسه بر اساس تابع هزینه (loss function / cost function) صورت می پذیرد. در این مرحله باید مقادیر وزن ها و بایاس های شبکه بر اساس این خطا آپدیت شوند.

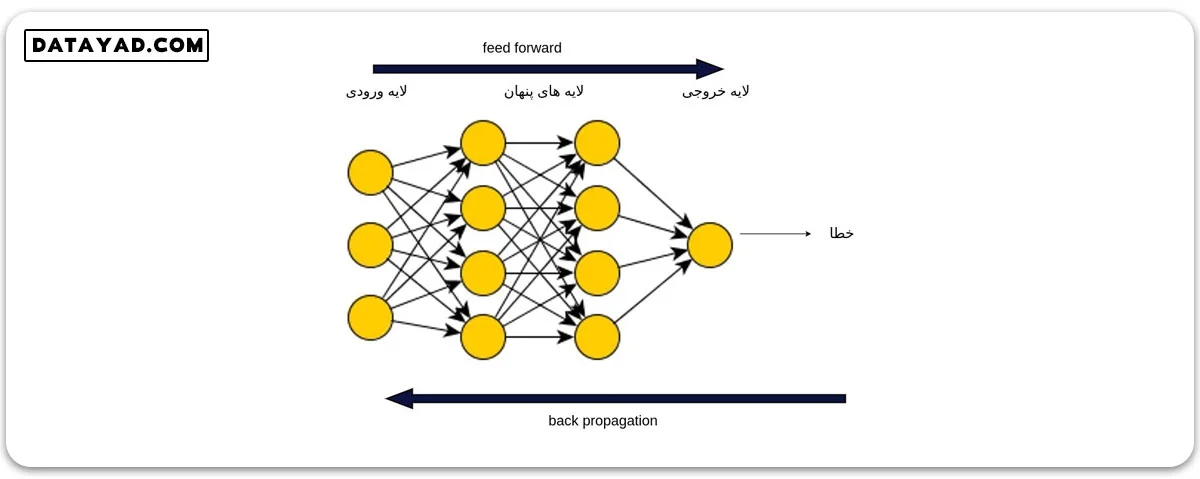
مفهوم feed forward و پس انتشار (back propagation)

به مرحله ای که طی آن ورودی ها در شبکه انتشار می یابند تا خروجی های شبکه تولید شوند، اصطلاحا feed forward می گوییم. در واقع میزان خطا، در انتهای فرایند feed forward تعیین می شود. سپس نوبت مرحله پس انتشار (back propagation) است. طی این مرحله، خطا به ترتیب از انتهای شبکه به سمت ابتدای آن توزیع می شود. در این مرحله ما به دنبال بهبود وزن ها و بایاس ها هستیم.

نحوه انجام پس انتشار خطا در یک شبکه عصبی

حال می خواهیم ببینیم خطا چطور توزیع می شود و پس از آن وزن ها و بایاس ها چطور آپدیت می شوند. توضیحات این قسمت بیشتر ریاضیاتی است و می توانید با مروری سطحی از آن عبور کنید. اما درک بهتر این ریاضیات به درک بهتر شبکه عصبی کمک می کند.

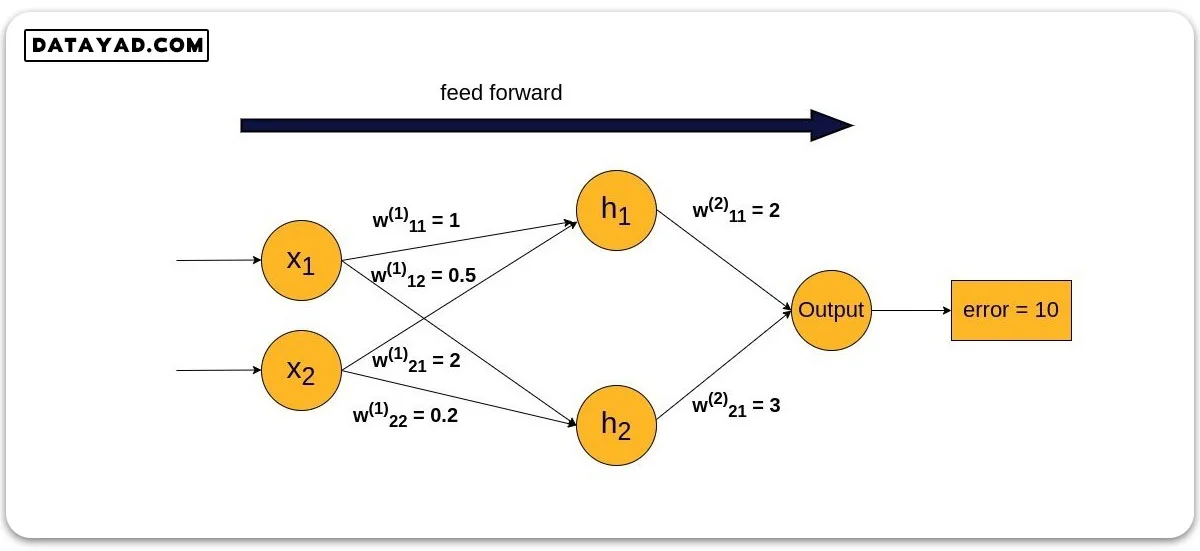
ابتدا با در نظر گرفتن مثالی ساده و عددی، مفهوم پس انتشار خطا را بیان می کنیم و سپس در بخش بعدی به فرمول بندی ریاضی در حالت کلی می پردازیم.

شبکه ساده ای را در نظر بگیرید که تنها یک لایه پنهان، یک خروجی و دو ورودی دارد. فرض کنید مقادیر وزن در مرحله feed forward به صورت زیر باشند و در پایان این مرحله به خطای ۱۰ واحد رسیده باشیم:

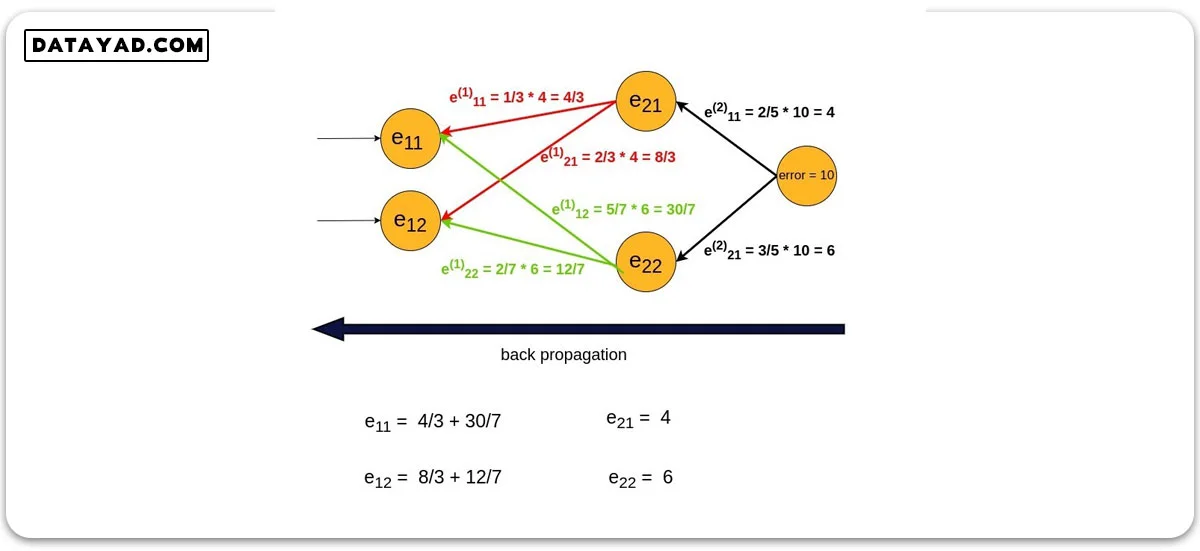
در این مرحله نوبت به فرایند پس انتشار، یعنی توزیع این خطا در شبکه تا رسیدن به لایه ورودی می رسد. به عبارت دیگر این خطای ۱۰ واحدی باید در تمامی گره های شبکه تقسیم شود. 

در هر گره، میزان خطا بین تمامی فلش های خارج شده از گره مربوطه تقسیم می شود. دقت کنید که این بار مسیر برگشت، یعنی از خروجی به سمت ورودی طی می شود. 

این تقسیم شدن با توجه به ضریب وزنی مربوطه صورت می گیرد. به بیان دیگر، هر فلش به میزان وزنی که دارد خطا دریافت می کند.

همچنین برای محاسبه خطای هر گره، مجموع خطاهایی که توسط فلش های مختلف به گره مربوطه وارد شده اند را حساب می کنیم. نکته دیگری که باید به آن دقت کنیم اینست که مجموع خطای هر لایه باید با خطای نهایی شبکه (در این مثال ۱۰) برابر باشد.

در انتهای مرحله پس انتشار، شبکه ما خطای نهایی را بین گره های خود توزیع کرده است. حال بر اساس خطای هر گره، وزن ها و بایاس ها آپدیت می شوند.

برای درک بیشتر این بخش پیشنهاد می کنیم کتاب شبکه عصبی تان را بسازید (make your own neural network) را بخوانید. ما خلاصه این کتاب فوق العاده را نیز در سایت دیتا یاد برای شما قرار داده ایم، برای مطالعه، روی عکس زیر کلیک کنید:

محاسبه رابطه گرادیان برای آپدیت وزن ها و بایاس ها در شبکه عصبی

در مبحث رگرسیون خطی، پس از محاسبه خطا، گرادیان را حساب کرده و از روی این گرادیان حساب شده می فهمیدیم که مقادیر وزن و بایاس را باید به کدام جهت تغییر دهیم. در این حالت، یک مسأله خطی ساده داشتیم که گرادیان های آن هم به سادگی قابل حل بود.

در بحث شبکه عصبی هم دقیقا مشابه همین روند اتفاق می افتد. در این جا هم خروجی هر گره یک مقدار y است که تابعی از وزن ها و بایاس های مربوطه است. در هر گره بر حسب y مربوطه و خطای همان گره، گرادیان را محاسبه کرده و وزن ها و بایاس ها را آپدیت می کنیم.

تفاوت عمده ای که در شبکه عصبی نسبت به رگرسیون خطی ساده وجود دارد، وجود تابع غیرخطی فعالسازی است که در واقع خروجی های y در هر گره، خروجی همین تابع فعالسازی هستند. به عنوان مثال اگر تابع فعالسازی ما سیگموید باشد، داریم:

در نتیجه تنها، مشتق گیری از حاصل جمع وزنی کافی نیست و باید از تابع فعالسازی هم مشتق گیری شود. به همن دلیل است که یکی از شروط تابع مورد استفاده به عنوان تابع فعالسازی این است که مشتق پذیر باشد.

مانند رگرسیون خطی، در نهایت ما به دنبال مشتق تابع هزینه L نسبت به وزن ها و بایاس ها هستیم. به عنوان مثال اگر روابط را برای ضرایب وزن باز کنیم، در نهایت هدف ما محاسبه (_wL(w▽ است. با مشتق گیری جزئی و با استفاده از قانون مشتق زنجیره ای داریم:

برای ساده سازی، دو جزء اول مشتق جزئی فوق را delta می نامیم و در فرایند آپدیت وزن ها و بایاس به عنوان یک ضریب از آن استفاده می کنیم:

واضح است که در رابطه بایاس ضریب x_i ظاهر نمی شود.

برای بررسی دقیق تر و توضیحات و درک بیشتر این روابط ریاضیاتی و محاسبات، ویدیوی این جلسه در ابتدای همین صفحه را حتما ببینید.

همان طور که گفتیم مشتق تابع فعالسازی در فرایند گرفتن گرادیان تابع هزینه ظاهر می شود و بنابراین مشتق پذیر بودن این تابع یک شرط حیاتی است. به عنوان مثال مشتق تابع سیگموید برابر است با:

مفهوم تکرارشونده (iterative) بودن شبکه عصبی

تمام مراحلی که در بالا گفتیم، حاصل، یک بار feed forward و سپس یک بار پس انتشار بود. در واقع تمام توضیحات بالا یک چرخه شبکه عصبی را نشان می دهد. این چرخه بارها و بارها در شبکه عصبی طی می شود تا به نقطه بهینه مد نظرمان برسیم.

به عبارت دیگر شبکه عصبی، یک الگوریتم تکرارشونده است. طی هر بار تکرار این چرخه، وزن ها و بایاس ها آپدیت شده و مجدد در شبکه به سمت خروجی انتشار می یابند و مقدار جدیدی برای خطا به دست می دهند.

با هر بار آپدیت این ضرایب، انتظار داریم شبکه به نقطه بهینه خود نزدیک تر شود تا جایی که به انتهای فرایند آموزش شبکه برسیم؛ جایی که با تنظیمات موجود، به دست آوردن خطای کمتر ممکن نباشد.