در جلسه هشتم از آموزش رایگان شبکه عصبی می خواهیم در مورد بهینه سازها (optimizers) در شبکه عصبی صحبت کنیم که این موضوع رو در دو قسمت هفت و هشت مورد بررسی قرار خواهیم داد.
بررسی دقیق تر مفهوم بهینه سازها (Optimizers) در شبکه عصبی
بهینه ساز (optimizer) الگوریتمی است که وزن ها و بایاس ها را در جهت بهبود خطا بهینه می کند. تا اینجا درباره بهینه ساز گرادیان کاهشی (Gradient Descent) صحبت کردیم. اما گرادیان کاهشی ضعف هایی داشت که باعث شد روش های اصلاح شده دیگری برای بهینه سازی معرفی شوند. از آنجایی که گرادیان کاهشی الگوریتم بسیار قدرتمندی است، این روش ها همگی بر اساس همان روش گرادیان کاهشی توسعه یافتند.
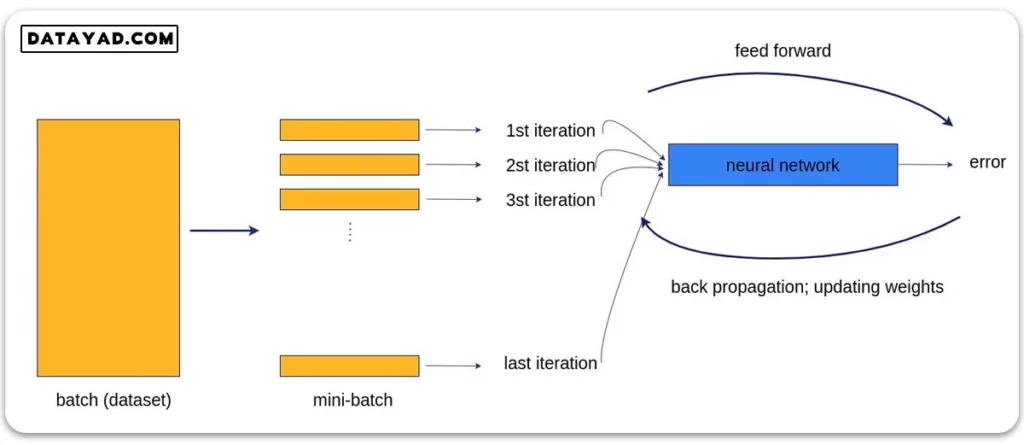
یکی از ضعف های الگوریتم گرادیان کاهشی این بود که کل دیتاست را یک جا بررسی کرده و بر اساس آن آپدیت را انجام می داد. همان طور که در جلسه پیش گفتیم این روش بسیار هزینه بر و کند است، مموری بسیار زیادی نیاز دارد و امکان استفاده از پردازش موازی را محدود می کند. به همین دلیل مفهوم دسته بندی دیتا (mini-batch) معرفی شد. در این حالت از بهینه سازهای دیگری استفاده می کنیم.
الگوریتم گرادیان کاهشی تصادفی (Stochastic Gradient Descent – SGD)
یکی از بهینه سازهایی که با داشتن mini-batch می توانیم از آن استفاده کنیم، گرادیان کاهشی تصادفی (Stochastic Gradient Descent) است. روش محاسبه گرادیان در این الگوریتم دقیقا مشابه گرادیان کاهشی (Gradient Descent) است. اما بر خلاف روش گرادیان کاهشی که کل دیتاست را یک باره به شبکه می دهد، الگوریتم گرادیان کاهشی تصادفی دسته های کوچک داده (mini-batch) را برای هر مرحله از بهینه سازی در نظر می گیرد.
به این ترتیب هر بار با یک mini-batch چرخه آموزش شبکه (feed-forward / back propagation) را انجام داده و با الگوریتم SGD وزن ها و بایاس ها را آپدیت می کنیم. سپس این فرایند برای دسته های بعدی انجام می شود تا جایی که شبکه کل دیتاست را ببیند و یک epoch کامل طی شود.
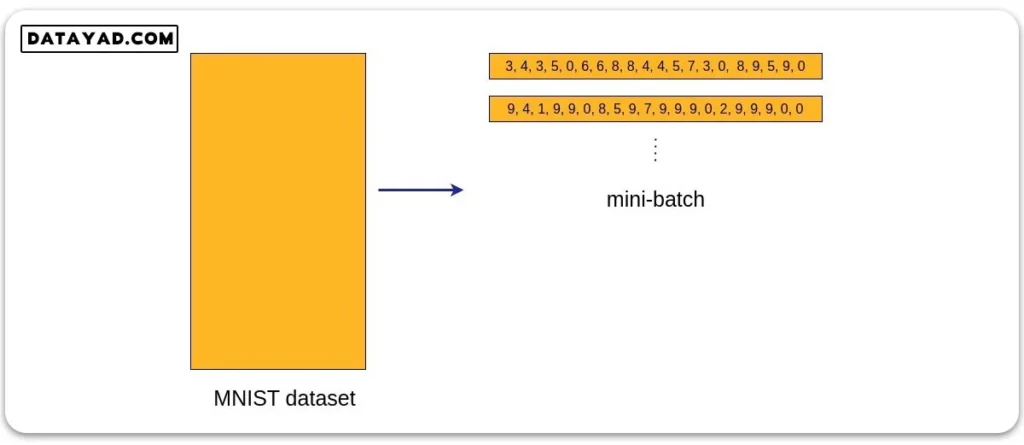
حال می خواهیم ببینیم واژه تصادفی (Stochastic) در نام این الگوریتم از کجا می آید. به عنوان مثال دیتاست MNIST را در نظر بگیرید که شامل اعداد دست نویس از صفر تا ۹ است و یک مسأله دسته بندی ده کلاسه را تعریف می کند. در شکل زیر چند نمونه از تصاویر این دیتاست نشان داده شده است.
فرض کنید batch_size را برابر ۲۰ در نظر گرفته ایم. به این ترتیب هر mini-batch شامل ۲۰ نمونه از دیتاست خواهد بود. اما از آنجایی که این داده ها برای هر دسته به صورت تصادفی انتخاب می شوند، ممکن است در چرخه اول تعدادی از داده ها اصلا دیده نشوند. به عنوان مثال اگر ۱ و ۲ در دسته داده اول نباشند، به این معناست که در چرخه اول ۱ و ۲ اصلا دیده نمی شوند.
از طرفی، عکس این حالت نیز ممکن است اتفاق بیفتد. یعنی در یک دسته داده، تعداد زیادی از داده ها متعلق به یک کلاس باشند. در این صورت شبکه روی این کلاس تمرکز زیادی کرده و به خوبی آموزش می بیند. اما روی باقی کلاس ها عملکرد خوبی نخواهد داشت.
این مشکلات باعث ایجاد سوگیری هایی در مدل می شود که به هیچ وجه مطلوب نیست. مثالی از این دو دسته داده دردسرساز برای مدل در شکل زیر نشان داده شده است. در این شکل در دسته اول مدل اصلا آموزشی روی کلاس های ۱ و ۲ نمی بیند و در دسته دوم مدل روی کلاس های ۹ و صفر بایاس می شود.
حال اگر در همه ایپاک ها، دیتاست را با یک ترتیب یکسان تقسیم بندی کنیم و در تمامی ایپاک ها، دسته ها به همین شکل باشند، این سوگیری در مدل نهایی وجود خواهد داشت که یک ایراد اساسی برای مدل است. به همین دلیل انتخاب mini-batch را تصادفی در نظر گرفتند تا این دسته ها در هر ایپاک به صورت تصادفی انتخاب شوند. به این ترتیب SGD معرفی شد. واژه تصادفی اشاره به انتخاب تصادفی دسته های داده دارد.
تفاوت الگوریتم های گرادیان کاهشی و گرادیان کاهشی تصادفی
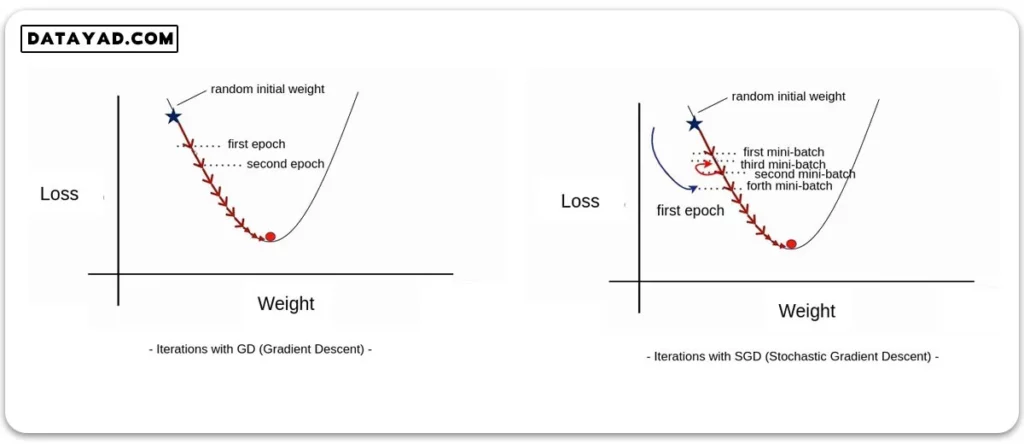
در شکل زیر تفاوت گرادیان کاهشی با گرادیان کاهشی تصادفی قابل مشاهده است.
در هر دوی این الگوریتم ها از روش گرادیان کاهشی برای بهینه سازی استفاده می شود. تنها تفاوت در اینست که در الگوریتم SGD، هر epoch شامل چرخه ای روی تمام دسته های کوچک است و پس از طی هر یک دور این چرخه که مدل یک mini-batch را می بیند، یک مرحله بهینه سازی داریم.
در مثالی که در این شکل و در نمودار سمت راست نشان داده شده، دیتاست به چهار دسته تقسیم شده و هر ایپاک شامل ۴ تکرار (iteration) است. همان طور که روی شکل سمت راست مشخص است، برخی از دورهای این چرخه ممکن است شامل دسته های نامناسبی از دیتا بوده و در مجموع ما را به سمت loss های پایین تر سوق ندهند. مثلا در این شکل، mini-batch سوم وزن ها را در جهتی آپدیت کرده که موجب افزایش loss شده است.
برخلاف SGD، در الگوریتم GD همان طور که در شکل سمت چپ مشاهده می شود، در هر ایپاک یک بار کل دیتاست دیده می شود و دیگر داخل ایپاک ها چرخه تکرار شونده ای روی دسته ها نداریم.
مشکل الگوریتم های گرادیان کاهشی و گرادیان کاهشی تصادفی
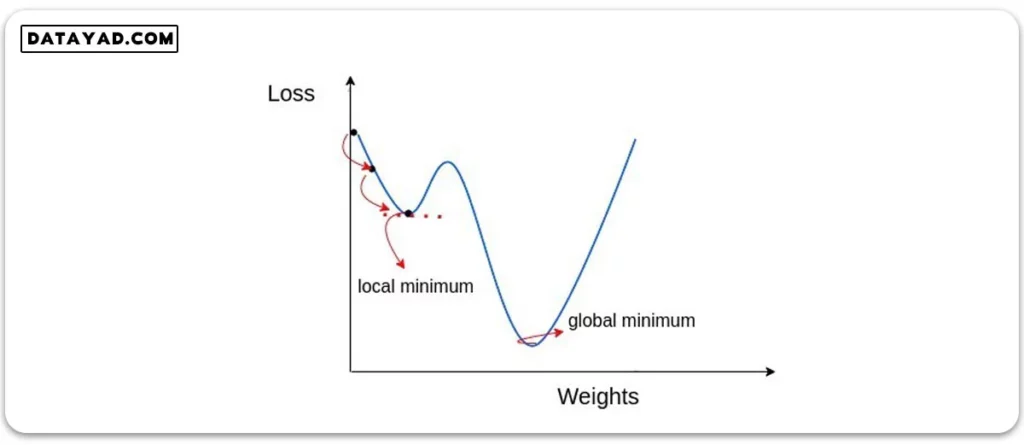
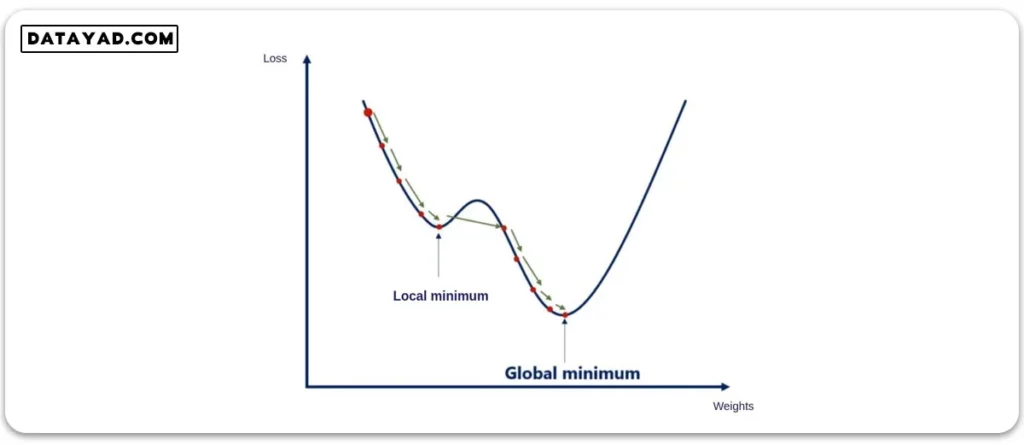
هر دوی این روش ها یک مشکل اساسی دارند؛ اینکه اغلب در کمینه محلی (local minimum) گیر می کنند. اگر نمودار تابع هزینه بر حسب وزن ها به شکل زیر باشد، هر دوی این الگوریتم ها با رسیدن به نقطه کمینه محلی (local minimum) متوقف شده و آن را به عنوان نقطه بهینه مسأله می بینند. در صورتی که هدف اصلی مسأله رسیدن به نقطه کمینه سراسری (global minimum) است.
برای حل این مسأله ایده مومنتوم (momentum) مطرح شد تا الگوریتم بتواند از قله محلی پیش روی خود عبور کرده و بدین ترتیب به کمینه سراسری (global minimum) برسد.
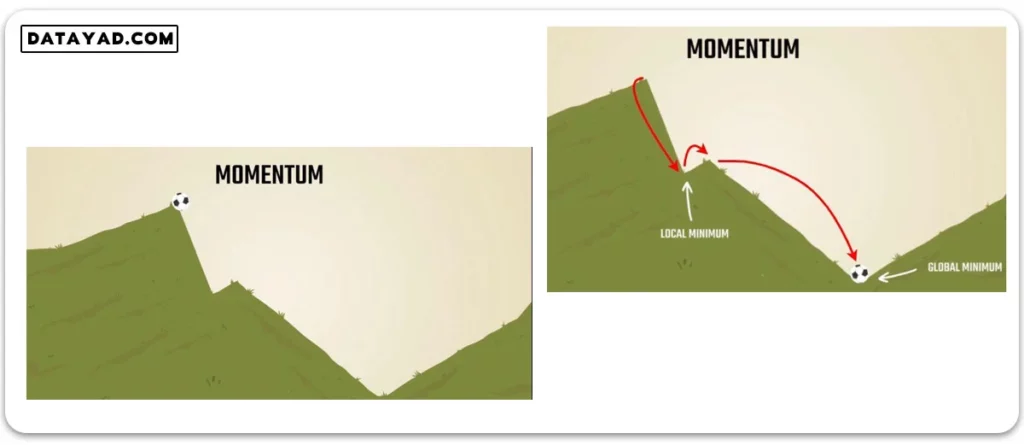
تکانه (momentum) در مسأله بهینه سازی
کارکرد این ایده در شبکه عصبی، دقیقا مشابه مفهوم مومنتوم در فیزیک است. فرض کنید توپی را از بالای تپه ای به شکل زیر رها می کنیم. با رسیدن به دره اول، اگر توپ در برخورد به ته این دره، سرعت رو به بالای لازم را برای رد کردن قله کوچک پیش روی خود داشته باشد، می تواند از این قله عبور کرده و به سطح زمین که پایین ترین نقطه دره است برسد.
برای پیاده سازی ایده ای مشابه در مسأله بهینه سازی، می توان تاریخچه حرکت را تا رسیدن به نقطه کمینه محلی (local minimum) در نظر گرفت. با بررسی گام های حرکتی تا پیش از این نقطه، می توان قدرت حرکت را در زمان رسیدن به کمینه محلی (local minimum) به دست آورد.
بسته به میزان قدرت و سرعت در لحظه ای که به نقطه کمینه محلی (local minimum) می رسیم، می توانیم روی نمودار از این نقطه پیش تر برویم. اگر این نقطه کمینه محلی (local minimum) باشد، سرعت اولیه می تواند الگوریتم را از گیر کردن در این نقطه نجات داده و با عبور از قله کوچک پیش رو، آن را به سمت کمینه سراسری (global minimum) سوق دهد.
در واقعیت معمولا نمودار ما تعداد زیادی کمینه محلی دارد. اگر نرخ یادگیری (learning rate) به حد کافی بزرگ باشد، معمولا کمینه های محلی کوچک را رد می کند. اما کمینه های محلی عمیق تر را معمولا نمی توان با نرخ یادگیری رد کرد و راه حل این مشکل در تکانه (momentum) است.
اضافه کردن تکانه (momentum) به الگوریتم بهینه سازی
برای پیاده سازی مومنتوم (momentum) در فرایند بهینه سازی، به الگوریتم گرادیان کاهشی حافظه ای اختصاص دادند تا به مقدار گرادیان در قدم های قبلی دسترسی داشته باشد. به عبارت دیگر در هر نقطه از نمودار، علاوه بر شیب خط مماس در همان نقطه، به مقدار این شیب در قدم های قبلی طی شده نیز دسترسی داریم.
به این ترتیب به جای اینکه در رابطه آپدیت وزن، فقط گرادیان در همان نقطه وارد شود، گرادیان قدم قبلی هم به عنوان تکانه وارد شده از گام های قبل با این مقدار جمع می شود. در نتیجه در هر گام برای آپدیت وزن ها و بایاس ها، تکانه حاصل از گام های پیشین هم لحاظ می شود.
ضریب آلفا در این رابطه، هایپرپارامتریست که به وسیله آن می توانیم تعیین کنیم میزان دخالت تکانه (momentum) در آپدیت وزن ها و بایایس ها چقدر باشد و چه میزان از مسیر حرکت قبلی را در حافظه خود قرار دهد.
اگر این مقدار را برابر صفر در نظر بگیریم، همان الگوریتم SGD را خواهیم داشت و هیچ حافظه ای از گذشته در کار نیست. به میزانی که این مقدار افزایش یابد، تاثیر تکانه در رابطه SGD افزایش می یابد.
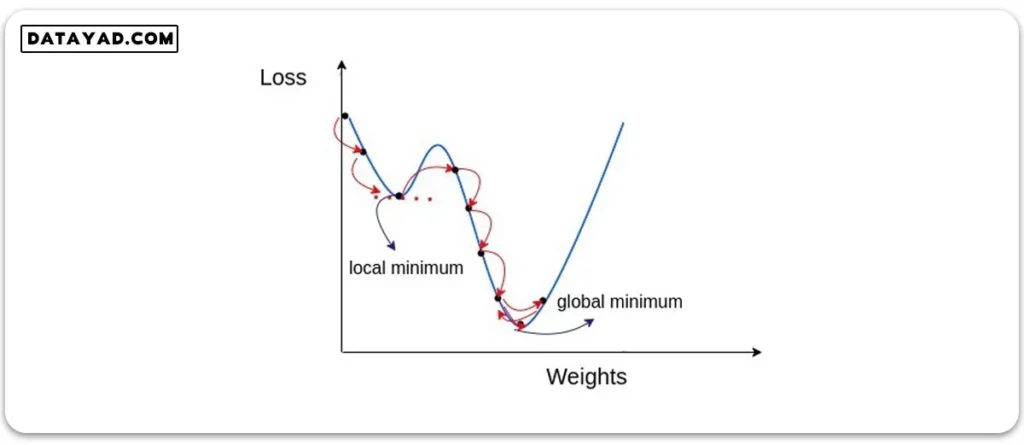
به این ترتیب الگوریتم ما می تواند در نقاط کمینه محلی (local minimum) از قله های کوچکی که پیش رویش قرار دارد به راحتی عبور کرده و به کمینه سراسری (global minimum) برسد. با رسیدن به نقطه کمینه محلی (local minimum)، تکانه موجود کمی آن را به سمت جلو سوق می دهد و پس از چند رفت و برگشت، سرانجام در نقطه کمینه سراسری (global minimum) متوقف می شود.
ایده تکانه (momentum) ایده بسیار مهمی است که کمک می کند کمینه سراسری را پیدا کرده و در کمینه محلی متوقف نشویم. همچنین پیش تر دیدیم مشکل مموری و سرعت فرایند آموزش با ایده mini-batch حل شد. اما کماکان مشکلاتی وجود دارد که در جلسات بعد بررسی خواهیم کرد و خواهیم دید که چطور دیگر الگوریتم های بهینه سازی به آپدیت وزن ها و بایاس ها کمک می کنند.



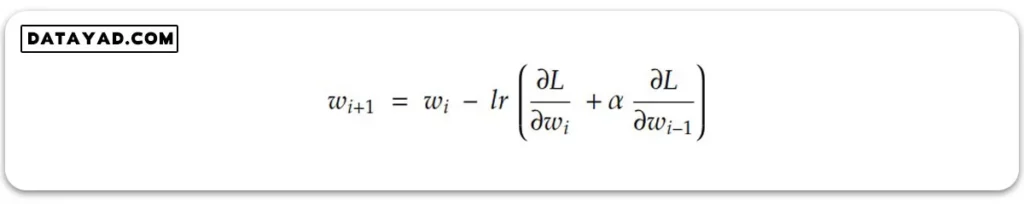





















2 پاسخ
نحوه بیان تون خیلی جالب و عالی هست. ممنون
ممنونم از بازخورد ارزشمندتون