در این مطلب می خواهیم در مورد کاربرد ریاضی در هوش مصنوعی و دلایل اهمیت آن برای پیشرفت در حرفه هوش مصنوعی صحبت کنیم. آینده ای که در فیلم های علمی تخیلی دیده ایم، هم اکنون اینجاست.
از واقعیت مجازی (VR) گرفته تا گجت های کاربردی، هوش مصنوعی به بخش های متنوعی از زندگی ما ورود پیدا کرده است، به روش هایی که هیچکس پیش از این ندیده بود یا انتظارش نمی رفت. چت بات ها و ابزارهای هوش مصنوعی در این دنیای تکنولوژی که هر روز تغییر می کند، مدت هاست که در آستانه تحولی عظیم بوده اند.
واقعیت این است که هوش مصنوعی، سحر و جادو نیست؛ صرفا ریاضیات است.
ایده های زیربنایی ماشین های متفکر و توانایی تقلید رفتار انسانی، همه به کمک مفاهیم ریاضی محقق می شوند. هوش مصنوعی (AI) و ریاضیات، شاخه هایی از یک درخت هستند و اگر شما می خواهید در حرفه ی خود در حوزه هوش مصنوعی پیشرفت کنید، لازم است که منابع معتبر آموزش هوش مصنوعی و ریاضیات هوش مصنوعی را بخوانید. اینکه صرفا طرفدار ژانر علمی تخیلی باشید، کافی نیست.
اگر می خواهید در حوزه هوش مصنوعی یک حرفه ای باشید و بهترین شغل ها و سمت ها را به دست آورید، با ریاضیات رفیق شوید. این کار دنیای شما را متحول خواهد کرد.
در این مطلب می خواهم رابطه جادویی بین هوش مصنوعی و ریاضیات را برای شما توضیح دهم. پس بیایید وارد این دنیای شگفت انگیز ریاضیات و هوش مصنوعی شویم.
«ریاضیات زبانی است که خداوند، جهان را با آن نوشته است.» – گالیلئو گالیله
ارتباط بین هوش مصنوعی و ریاضیات چیست؟
ریاضیات هوش مصنوعی یکی از اصول تکنولوژیهای ماشینی است. زیرا تمامی مدلها و الگوریتمهای مورد استفاده در هوش مصنوعی بر پایه مفاهیم و اصول ریاضی بنا شدهاند. ریاضیات هوش مصنوعی نقش اساسی در تحلیل دادهها، مدلسازی، طراحی الگوریتمها و حتی تفسیر نتایج آنان دارند. در واقع، میتوان گفت پیادهسازی پروژه هوش مصنوعی بدون مفاهیم ریاضی امکانپذیر نیست.
یکی از مهمترین کاربردهای ریاضیات هوش مصنوعی، مدلسازی دادهها است. دادهها در هوش مصنوعی معمولاً به صورت ماتریسها و بردارها نمایش داده میشوند که این موارد بر پایه جبر خطی عمل میکنند. برای مثال، در پردازش تصویر، هر عکس به صورت ماتریسی از پیکسلها نمایش داده میشود و در پردازش زبان طبیعی، کلمات به بردارهایی در فضای چندبعدی تبدیل میشوند.در حوزه حسابداری نیز، کاربرد هوش مصنوعی در حسابداری به کمک مدلسازیهای ریاضی، امکان تحلیل دقیقتر دادههای مالی و پیشبینی روندهای اقتصادی را فراهم میسازد.
مشکلات و مسائل حوزه هوش مصنوعی، در دو دسته بندی کلی قرار می گیرند:
- مشکلات جستجو (search)
- مشکلات نمایش (representation)
در ادامه هم مواردی همچون مدل های به هم پیوسته و ابزارهایی مثل:
- قواعد (Rules)،
- فریم ها (Frames)،
- منطق ها (Logics)
- و Netها…
تمام این ها، موضوعاتی ریاضی هستند.
هدف اصلی هوش مصنوعی، ایجاد مدلی قابل قبول از درک انسانی است و این مدل ها را می توان با استفاده از ایده ها و استراتژی هایی از زیرشاخه های متنوع ریاضیات آماده کرد.
مثلا اتومبیل های خودران (self-driving) را در نظر بگیرید. هدف این است که این ماشین ها، اجسام و افراد را در تصاویر ویدیویی، تشخیص دهند. در این خودروها، از ریاضیات استفاده شده است، مواردی مثل روندها و روش های کمینه سازی (minimization) و پس انتشار (back-propagation یا انتشار معکوس).
ریاضیات به دانشمندان هوش مصنوعی کمک می کند که مشکلات پیچیده انتراعی و چالش برانگیز را با استفاده از روش های سنتی و تکنیک هایی حل کنند که قرن هاست ریاضیدان ها از آن ها بهره می گیرند.
مباحث ریاضیات هوش مصنوعی
زیربنای تمام پیشرفت های مهم و قابل توجه، ریاضیات است. مفاهیمی همچون جبر خطی، حساب دیفرانسیل و انتگرال، نظریه بازی، آمار و احتمالات، رگرسیون های لجستیک پیشرفته و کاهش گرادیان، همه زیربناهای اصلی علم داده محسوب می شوند. بد نیست بدانیم که دانش ریاضی در علم داده اهمیت بالایی دارد.
ریاضیات به درک استدلال منطقی و توجه به جزییات کمک می کند. ریاضیات، توانایی های شما را بهبود می بخشد تا بتوانید در شرایط تحت فشار، بهتر فکر کنید و استقامت ذهنی شما را افزایش می دهد.
مفاهیم ریاضی، راه حلی واقعی برای مشکلات مجازی یا فرضی ارائه می کند. موضوع اصلی ساختار است، ایجاد کردن و توسعه اصول و قواعدی که همیشه درست (true) هستند، حتی اگر در اجزا، تغییری ایجاد شود.
میتوان بیان کرد که مباحث ریاضیات هوش مصنوعی شامل جبر خطی، احتمال و آمار، حساب دیفرانسیل و انتگرال و بهینهسازی است. جبر خطی برای نمایش دادهها به صورت بردارها و ماتریسها و انجام محاسبات در لایههای مختلف شبکههای عصبی به کار میرود. احتمال و آمار نیز برای مدیریت شرایطی که عدم قطعیت وجود دارد، استفاده میشود. همچنین حساب دیفرانسیل و انتگرال در محاسبات گرادیان و الگوریتمهای بهینهسازی کاربرد دارد.
سه زیرشاخه اصلی ریاضیات که باعث پیشرفت در حرفه هوش مصنوعی می شوند و یک متخصص هوش مصنوعی باید آنها را بلد باشد، عبارتند از:
✔️ جبر خطی
✔️ حساب دیفرانسیل و انتگرال
✔️ احتمالات
در ادامه میخواهیم هر سه مورد از این مباحث ریاضی در هوش مصنوعی را با هم بررسی کنیم.
مفاهیمی مانند جبر خطی، آمار و احتمال، حساب دیفرانسیل و بهینه سازی از ارکان اصلی الگوریتمهای هوش مصنوعی به شمار میآیند. برای یادگیری اصولی و کاربردی این مباحث، پیشنهاد میکنیم در آموزش ریاضی برای هوش مصنوعی شرکت کنید.
جبر خطی (Linear Algebra)
جبر خطی، شاخه ای از ریاضیات کاربردی است که برای متخصصان هوش مصنوعی حیاتی است. اگر شما روی جبر خطی تسلط بالایی نداشته باشید، نمی توانید به متخصص خوبی در حوزه هوش مصنوعی تبدیل شوید. همانطور که سخنگوی Skyler می گوید:
«جبر خطی، ریاضیاتِ قرن بیست و یکم است.»
جبر خطی به تولید ایده های جدید کمک می کند، به همین دلیل است که یادگیری آن، برای متخصصان حوزه هوش مصنوعی ضروری است. این افراد می توانند با مفاهیم اسکالرها (نرده ها)، بردارها، تانسورها، ماتریس ها، مجموعه ها و توالی ها، توپولوژی، نظریه بازی، نظریه گراف، توابع، تبدیل های خطی، مقدار ویژه و بردار ویژه، داده ها و مدل ها را تجسم کنند.
یکی از کاربردهای اصلی جبر خطی در ریاضیات هوش مصنوعی، انجام محاسبات در شبکههای عصبی مصنوعی است. در هر لایه از یک شبکه عصبی، دادههای ورودی در یک ماتریس وزن ضرب شده و سپس یک بردار بایاس به آن اضافه میشود تا خروجی لایه تولید شود. این فرآیند به صورت معادله زیر بیان میشود:
B+X.W =Z
در فرمول بالا، X ورودی، W ماتریس وزنها، b بردار بایاس و Z خروجی لایه است.
– بردارها (وکتورها)
در برنامه نویسی خطی، از بردارها برای رسیدگی به نابرابری ها و دستگاه های معادلات برای راحتی نشانه ای استفاده می کنند. متخصصان هوش مصنوعی، از تکنیک های متفاوت بردارها برای حل مشکلات رگرسیون، خوشه بندی، بازشناسی گفتار و ترجمه ماشینی استفاده می کنند.
این مفاهیم همچنین برای نگهداری بازنمود داخلی مدل های هوش مصنوعی، همچون طبقه بندی خطی و شبکه های یادگیری عمیق مورد استفاده قرار می گیرند.
در شبکههای یادگیری عمیق، بردارها به عنوان ورودی، خروجی و حتی وزنهای هر لایه عمل میکنند و تمامی عملیات پیچیده ،از طریق محاسبات برداری و ماتریسی انجام میشود.
– نظریه ماتریس (Matrix Theory)
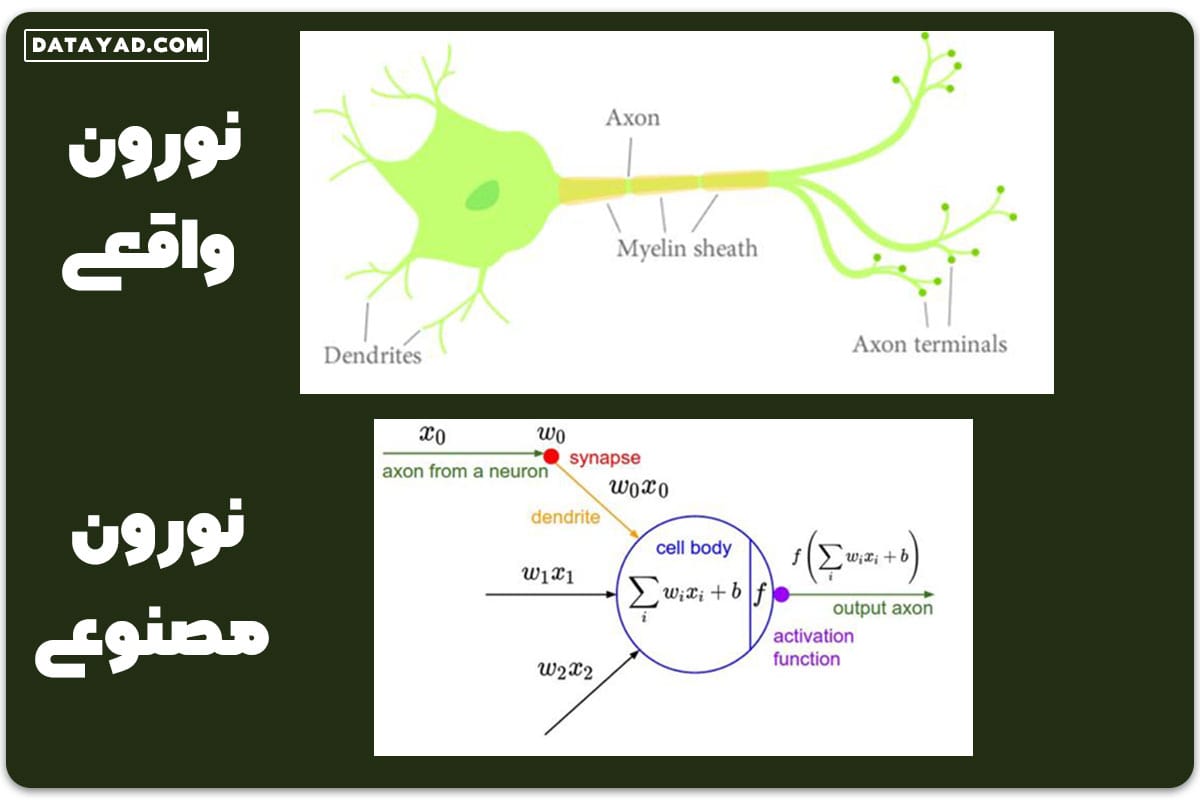
در فیلم های علمی تخیلی، معمولا شاهد این هستیم که با اجرای یک ساختار کامپیوتری – محاسباتی مشابه با سیستم عصبی، یک شبکه عصبی با ایجاد ارتباطاتی بین نورون ها برای تطبیق استدلال آن با مغز انسان ایجاد می شود. مفهوم ماتریس، در مطالعه شبکه های عصبی مورد استفاده قرار می گیرد.
یک فرضیه غیرخطی را می توان با شکل دادن نورون های مصنوعی در سه لایه زیر در شبکه عصبی محقق کرد:
- لایه ورودی: در این مرحله دادههای خام (مانند تصاویر، متن یا صدا) به شبکه وارد شده و به شکل بردار یا ماتریس برای پردازش آماده میگردند.
- لایه های پنهان: شامل مجموعهای از نورونهای مصنوعی است که از طریق ماتریس وزنها و توابع فعالسازی، ویژگیهای پیچیده دادهها را استخراج میکنند.
- لایه خروجی: این لایه نتیجه نهایی پردازش شبکه مانند پیشبینی یک دسته یا بازتولید دادههای ورودی را ارائه میدهد.
متخصصان هوش مصنوعی، شبکه های عصبی را با استفاده از تعداد لایه های پنهان آن ها و شیوه اتصال آن ها، طبقه بندی می کنند. شبکه عصبی می تواند با استفاده از این نورون های مصنوعی تشکیل شود و کشف کردن این مساله 20 سال طول کشید.
– مقدار ویژه و بردار ویژه
علمِ رتبه بندی در موتورهای جستجو، بر اساس علم ریاضیات است. رتبه صفحه یا پیجرنک (Page Rank)، که پایه و اساس تاسیس شرکتی مثل گوگل است، بر اساس یک رویکرد ریاضیاتی شکل گرفته است.
رتبه صفحه یک الگوریتم است، که اولین بار توسط لری پیج و سرگئی برین در مقاله تحقیقاتی آن ها با عنوان «آناتومی موتور جستجوی وب ابرمتنی مقیاس بزرگ» مطرح شد.
مفاهیم ابتدایی اصول مقدار ویژه و بردار ویژه، که بیش از صد سال است کشف شده، در دستیابی به این دستاورد بزرگ مورد استفاده قرار گرفته است.
خزنده های وب (crawlers) ابتدا صفحات وب را بازیابی می کنند، سپس با تخصیص دادن مقادیر رتبه صفحه (Page Rank)، صفحات را ایندکس و فهرست می کنند. اعتبار هر صفحه، به تعداد لینک های مرتبط به آن صفحه بستگی دارد.
رتبه r(P) برای صفحه P به شکل زیر در نظر گرفته می شود:
که:
Bp = تمام صفحاتی که به P اشاره می کنند
|Q| = تعداد لینک های خروجی از Q
P ماتریسی با این شرایط است:
برای یافتن همگرایی و نرخ های همگرایی، ماتریس P تنظیم می شود. وقتی که جمع ردیف ماتریس P گوگل به 1 می رسد، به آن ماتریس تصادفی راست (ردیف) گفته می شود. تکرار رتبه صفحه، نشان دهنده تحول یک زنجیره مارکوف است، که در آن گراف تحت وب، به عنوان یک ماتریس احتمال انتقال P نمایش داده می شود.
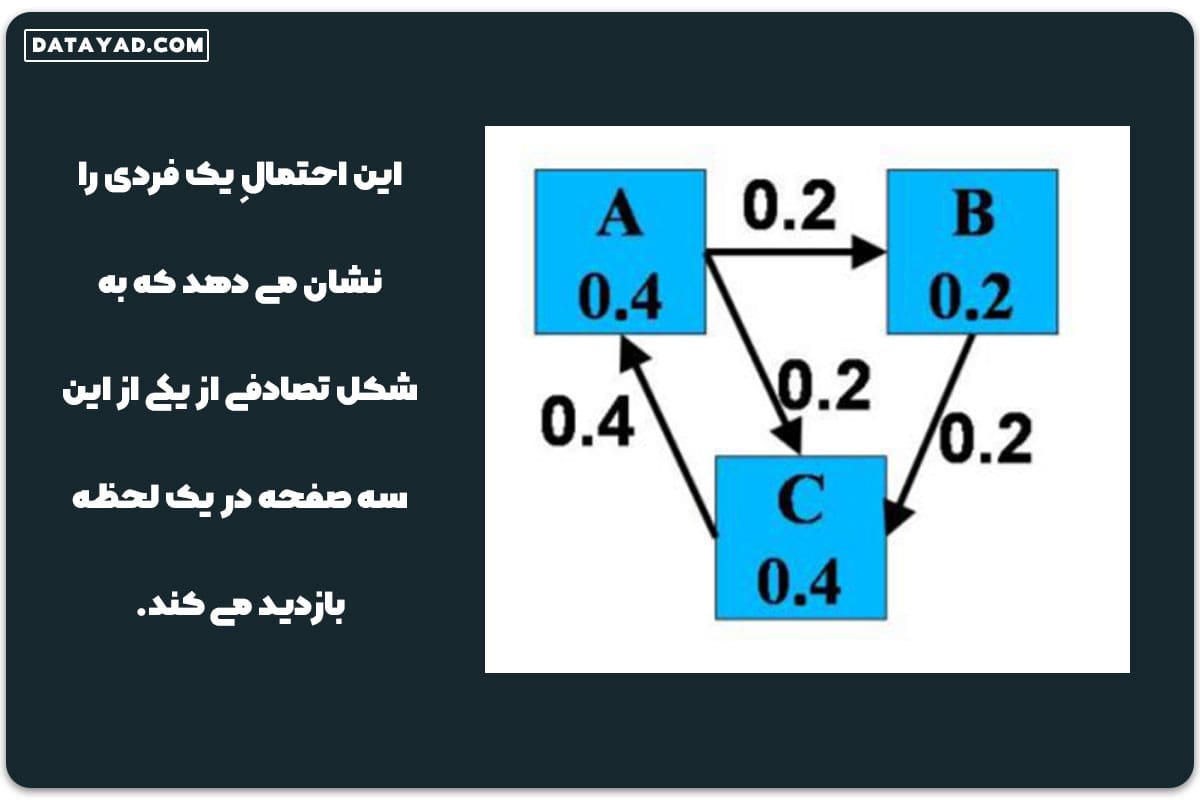
این احتمالِ یک فردی را نشان می دهد که به شکل تصادفی از یکی از این سه صفحه در یک لحظه بازدید می کند.
اول، یک ماتریس مجاورت برای نشان دادن ساختار لینک (link structure) ایجاد می شود، سپس با نرمال سازی آن، به یک ماتریس احتمال تبدیل می شود.
برای محاسبه رتبه صفحه (Page Rank)، حل کردن مشکل مقدار ویژه برای سیستم خطی، ضروری است.
مقادیرویژه ماتریس تصادفی P می تواند به شکل زیر در نظر گرفته شود:
1> λ1 ≥ λ2 ≥ … ≥ λn
و بردارهای ویژه مرتبط با آن ها V1, V2, V3, …, Vn خواهد بود.
بعد از فرآیند همگرایی، مقدارویژه غالب ماتریس P باید λ=1 باشد تا محقق شود:
با،
که توزیع حالت پایدار مدل مارکوف است. این مدل ریاضیات هوش مصنوعی، احتمال بازدید از هر صفحه را در درازمدت تعیین میکند و اساس محاسبه رتبه صفحه (PageRank) را فراهم میسازد.
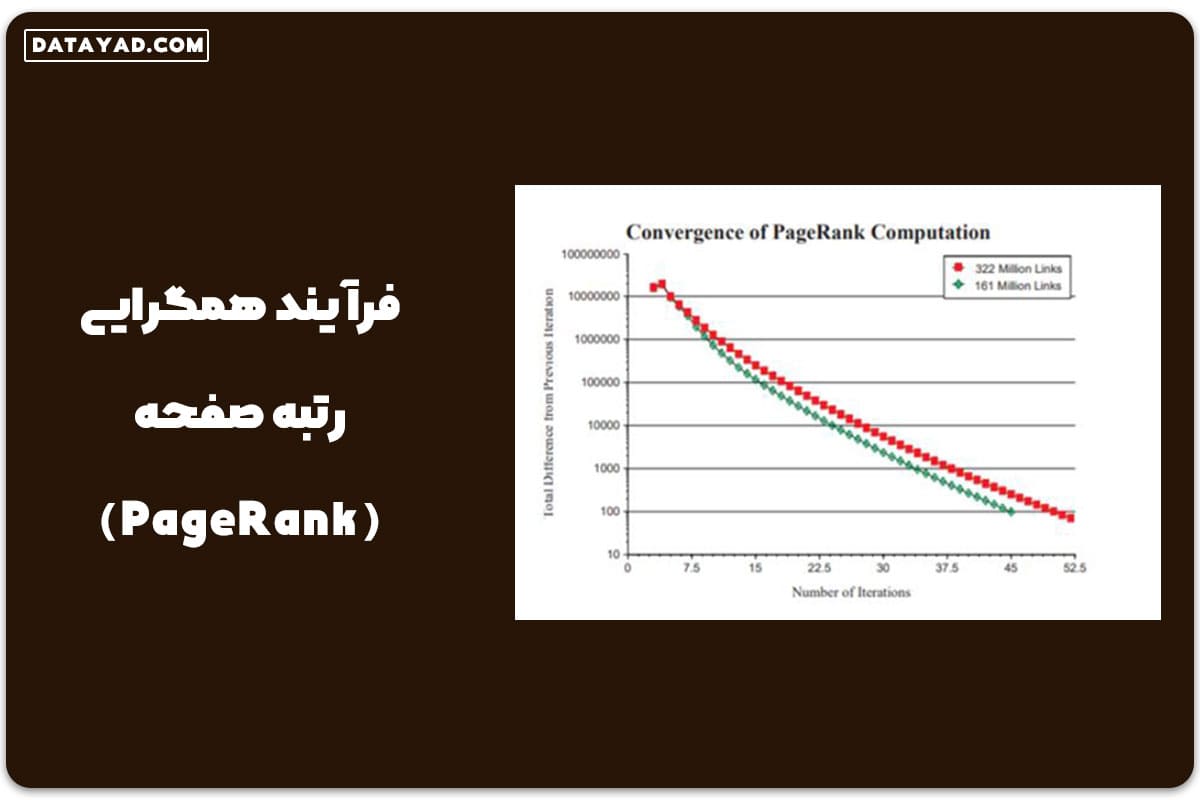
فرآیند همگرایی رتبه صفحه (PageRank) در گراف زیر نمایش داده شده است. گوگل به این روش، به شکل اتوماتیک و خودکار، مقدار Page Rank را برای هر سایت تعریف می کند.
حساب دیفرانسیل و انتگرال
حساب دیفرانسیل، حساب چندمتغیره، حساب انتگرال، کمینه سازی خطا و بهینه سازی با گرادیان کاهشی، حد یا لیمیت ها، رگرسیون لجستیک پیشرفته، همه مفاهیمی هستند که در مدلسازی ریاضی مورد استفاده قرار می گیرند.
یک مدل ریاضیاتی که به خوبی طراحی شده باشد، در علوم زیست پزشکی برای شبیه سازی فرآیندهای پیچیده بیولوژیکی سلامت و بیماری های انسانی، با دقت و کیفیت بالا استفاده می شود.
مدلسازی درونرایانهای (این سیلیکو یا In-Silico)، به کارگیری رویکردهای هوش مصنوعی در زیست پزشکی، یک مدل کاملا خودکارشده (automated) است که به نمونه و سمپل های انسانی، تست های خشن روی حیوانات، کارآزمایی های بالینی یا تجهیزات آزمایشگاهی نیازی ندارد.
یک معادله ریاضیاتی دیفرانسیل، در این مدل استفاده می شود تا فرضیه های مکانیستیکی جدید را تست کند و اهداف درمانی تازه را ارزیابی کند. این ارزان ترین و راحت ترین روش برای مطالعه و تحقیق روی فیزیولوژی انسان، واکنش به دارو و بیماری هاست، که با دستکاری و تغییر پارامترهای مدل ریاضیاتی، بسیار دقیق تر عمل می کند.
مثال:
فرض کنید یک تیم تحقیقاتی قصد دارد اثر یک داروی جدید روی کنترل قند خون در بیماران دیابتی را بررسی کند. به جای انجام آزمایشهای پرهزینه و زمانبر روی حیوانات یا بیماران انسانی، تیم از یک مدل ریاضیاتی مبتنی بر معادلات دیفرانسیل استفاده میکند.
این مدل ریاضیات هوش مصنوعی تغییرات سطح گلوکز خون را بر اساس پارامترهایی مانند نرخ جذب دارو، متابولیسم بدن و حساسیت انسولین شبیهسازی میکند. با استفاده از روش گرادیان کاهشی، تیم تحقیقاتی مدل را برای پیشبینی دقیقتر بهینهسازی میکند. سپس با تغییر مقادیر پارامترها، مانند دوز دارو یا زمانبندی مصرف، میتوان بهترین شرایط برای کاهش قند خون را بدون عوارض جانبی شناسایی کرد.
آمار و احتمالات
مشکلات انتزاعی زیادی در دنیای هوش مصنوعی وجود دارد، ممکن است با عدم قطعیت و مواردی غیر قابل پیش بینی و پراکنده در اشکالی مختلف روبرو شوید. نظریه احتمالات، ابزاری برای مقابله با عدم قطعیت ارائه می کند. برای تحلیل تناوب و تکرار رخ دادنِ یک رویداد، از مفاهیم احتمالات استفاده می شود، چون به عنوان شانسِ وقوع یک رویداد تعریف شده است.
مثلا یک ربات را در نظر بگیرید. یک ربات فقط می تواند برای چند ثانیه ی مشخص، به جلو حرکت کند، نه یک فاصله مشخص. برای اینکه این ربات به جلو حرکت کند، متخصصان در برنامه نویسی آن از ریاضیات استفاده می کنند. متغیرهای تصادفی گسسته، متغیرهای تصادفی پیوسته، فرمول یا قضیه بیز (Bayes) و نرمال سازی، چندی از مفاهیم احتمالات هستند که علاوه بر جبر خطی، در حرکت و هدایت و راهبری رباتیک استفاده می شوند.
آمار و احتمالات در یادگیری ماشین و بحث ریاضیات هوش مصنوعی، برای تخمین و پیشبینی رفتارهای سیستمهای پیچیده کاربرد دارند. با استفاده از مدلهای احتمالی، میتوان عدم قطعیتها را به شکل کمی تحلیل کرد و تصمیمگیریهای بهینهتری در هوش مصنوعی و رباتیک ، مانند پیشبینی مسیر یا شناسایی موانع انجام داد.
حل مسائل ریاضی با هوش مصنوعی
یک سری ربات ها و سایت ها هستند که مسائل ریاضی را با هوش مصنوعی برای شما حل می کنند که در اینجا می خواهیم به چند مورد از آنها اشاره کنیم.
✅ سایت cymath
✅ سایت mathway
✅ سایت wolframalpha
✅ سایت brilliant
✅ سایت Microsoft Math Solver
با توجه به موارد بیان شده در builtin سایتها و رباتهای مذکور نه تنها مسائل ساده ریاضیات هوش مصنوعی را حل میکنند، بلکه توانایی پاسخ به مسائل پیچیدهتر مانند معادلات دیفرانسیل، هندسه و محاسبات پیشرفته را نیز دارند.
کتاب ریاضیات هوش مصنوعی
یکی از بهترین کتاب های این حوزه، کتاب ریاضیات ضروری برای هوش مصنوعی (Essential Math for AI) اثر حلا نلسون هست که در سال 2023 به چاپ رسیده است. این کتاب 14 فصل دارد و به مباحث ریاضیات مورد نیاز در هوش مصنوعی می پردازد.
این کتاب ریاضیات هوش مصنوعی برای افرادی که در حوزه هوش مصنوعی و علم داده فعالیت دارند و می خواهند تفکر ریاضی خود را تقویت کنند، مناسب است.
نکته ای که باید در مورد این کتاب ریاضیات بدانید این است که این یک کتاب کدنویسی یا یک کتاب آموزش ریاضی نیست، بلکه تنها تأکید بر مفاهیم ریاضی، شهود و درک کلی مباحث مورد نیاز آن در هوش مصنوعی است.
همچنین، دانشجویان، پژوهشگران و مهندسانی که به دنبال تقویت دانش خود در حوزه ریاضیات هوش مصنوعی هستند، میتوانند از این کتاب بهرهمند شوند.
جمع بندی نهایی
اگر می خواهید در سطح حرفه ای، مهندس یادگیری ماشین، متخصص داده ها یا دانشمند رباتیک شوید، لازم است که در ریاضیات، عملکردی عالی داشته باشید. پیشنهاد می کنم کتاب ریاضیات برای یادگیری ماشین را بخوانید.
ریاضیات می تواند مهارت های تفکر تحلیلی را بهبود بخشد که در هوش مصنوعی حیاتی هستند. در واقع، ریاضیات هوش مصنوعی زیربنای تمامی الگوریتمها و فناوریهای پیشرفتهای است که در هوش مصنوعی و یادگیری ماشین به کار میروند. متخصصان هوش مصنوعی معمولا می گویند که از نظر افراد غیرمتخصص، هوش مصنوعی مثل جادوست، اما هوش مصنوعی جادو جمبل نیست، صرفا ریاضیاتی است که جادوی این ابداع و نوآوری ها را ایجاد می کند. بنابراین برای پیشرو بودن در دنیای هوش مصنوعی محور امروز، لازم است که ذوق و مهارتی عالی در ریاضیات داشته باشید. برای شروع، تمرینهایی مثل ساخت ماشین حساب با پایتون میتواند در درک بهتر مفاهیم ریاضی و آشنایی با منطق برنامهنویسی بسیار مؤثر باشد.
ریاضیات یکی از اصول پیشرفت در علم و فناوری محسوب میشود و در بسیاری از حوزهها، از مدلسازی دادهها گرفته تا یادگیری ماشین و هوش مصنوعی، کاربردهای فراوانی دارد. در این میان، پایتون به عنوان یکی از قدرتمندترین ابزارهای برنامهنویسی، نقش کلیدی در انجام محاسبات ریاضی و پیادهسازی الگوریتمهای پیشرفته ایفا میکند.. برای آشنایی بیشتر با مهمترین کاربردهای پایتون در زمینه ریاضیات، میتوانید مقاله مربوطه را مطالعه کنید.
آموزش پیشنهادی و مکمل
برای یادگیری کاربرد ریاضیات هوش مصنوعی و تقویت مهارتهای خود در این حوزه، منابع متنوعی در دسترس هستند. جهت مطالعه بیشتر، کتابهایی نظیر “Mathematics for Machine Learning” و “Deep Learning Illustrated” که به فارسی هم ترجمه شدهاند پیشنهاد میگردند زیرا مفاهیم ریاضی را به زبان ساده و با مثالهای کاربردی توضیح میدهند.
سوالات متداول
چگونه مفاهیم جبر خطی در طراحی و آموزش مدلهای یادگیری عمیق به کار میروند؟
در بحث ریاضیات هوش مصنوعی، مفاهیمی چون بردارها، ماتریسها و تجزیه مقدار منفرد (SVD) در یادگیری عمیق برای انجام محاسبات در لایهها و الگوریتمهای بهینهسازی استفاده میشوند. این عملیات، اساس محاسبات در شبکههای عصبی و الگوریتمهایی مانند مشتقگیری و گرادیان و پخش به عقب (Backpropagation) هستند.
چه نقشی مفاهیم احتمال و آمار در پیشبینی و تحلیل دادههای هوش مصنوعی دارند؟
احتمال و آمار در هوش مصنوعی برای مدلسازی در شرایط عدم قطعیت، تحلیل توزیع دادهها، پیشبینی نتایج، بهینهسازی مدلها و ارزیابی دقت آنها به کار میروند. این مفاهیم اساس الگوریتمهایی مانند یادگیری بیزین، رگرسیون و روشهای نمونهگیری را تشکیل میدهند.
چرا بهینهسازی (Optimization) یکی از اجزای کلیدی در هوش مصنوعی است و چگونه از آن استفاده میشود؟
الگوریتمهای بهینهسازی در ریاضیات هوش مصنوعی برای یافتن مناسبترین مقادیر پارامترهای مدل استفاده میشود تا خطای پیشبینی حداقل شود. این فرآیند با استفاده از روشهایی مانند مشتقگیری و گرادیان انجام میشود و دقت و عملکرد مدل را بهبود میبخشد.
چگونه معادلات دیفرانسیل در شبیهسازی شبکههای عصبی و دینامیک سیستمهای هوشمند به کار گرفته میشوند؟
معادلات دیفرانسیل برای مدلسازی تغییرات پیوسته استفاده میشوند. آنها در شبیهسازی فرآیندهای یادگیری، مدلهای پیوسته زمانی و تحلیل رفتار سیستمهای پیچیده مانند حافظه و یادگیری در شبکههای عصبی مورد استفاده قرار میگیرند.
اکنون با مطالعه این مقاله به اهمیت پایههای ریاضی در درک عمیقتر الگوریتمهای هوش مصنوعی پی بردهاید، پیشنهاد میکنیم در دوره ریاضی هوش مصنوعی شرکت کنید. در این دوره، مفاهیم کلیدی مانند جبر خطی، آمار و احتمال، و حسابان بهصورت گامبهگام آموزش داده شده و با مثالها و تمرینهای عملی در محیط پایتون پیادهسازی میشوند.





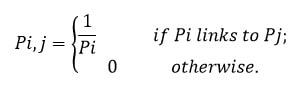
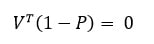
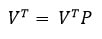
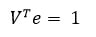























6 پاسخ
من همیشه از ریاضیات می ترسیدم، ولی تونستم با دوره ریاضیات شما ترسم یه بار واسه همیشه بریزه، ممنونم ازتون استاد عزیزم
خداروشکر، خیلی هم عالی
خیلی مفید و کاربردی بود، مرسی از شما
عزیزدلی ایمان جان
سلام وقت بخیر
ممنونم از مطلب مفید تون
در دوره علم داده ای که توی دیتایاد هست، ریاضیات هم تدریس میشه؟
بله ریاضیات یادگیری ماشین و علم داده، ریاضیات یادگیری عمیق و… به طور کامل و مفصل تدریس میشه، سرفصل های دوره رو توی لینک پایین می تونین به طور جرئی تر مشاهده کنید.
دوره علم داده