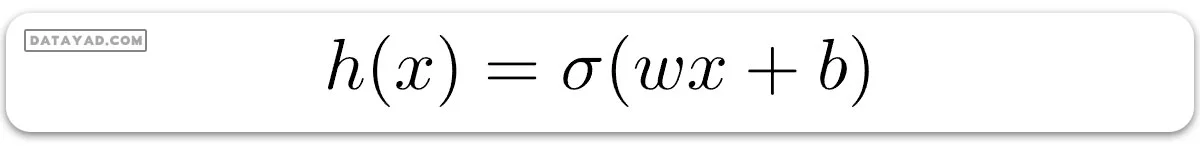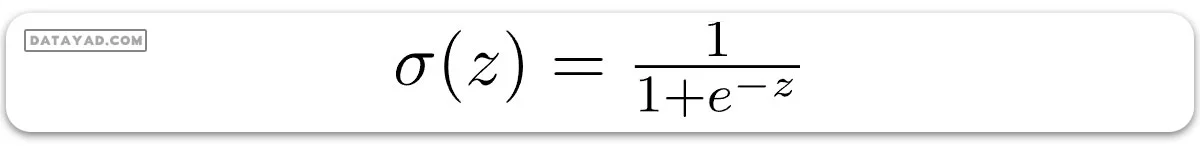رگرسیون لجستیک با استفاده از tensorflow

فهرست مطالب
در درس سی و چهارم از نیچ کورس آموزش رایگان یادگیری ماشین با پایتون می خواهیم در مورد رگرسیون لجستیک با استفاده از tensorflow صحبت کنیم.
رگرسیون لجستیک (Logistic Regression) یک الگوریتم طبقهبندی است که در یادگیری ماشین کاربرد زیادی دارد. این روش به ما امکان میدهد تا با یادگیری ارتباطات موجود در مجموعه دادههای دارای برچسب، دادهها را به دستههای مشخصی تقسیم کنیم. این الگوریتم ابتدا یک رابطه خطی از دادهها را یاد میگیرد و سپس با افزودن تابع غیرخطی سیگموئید، تغییری در آن ایجاد میکند.
در رگرسیون لجستیک، فرضیه ما سیگموئید یک خط راست است، به این صورت:
که در آن:
است. در این فرمول، بردار w وزنها و عدد b بایاس مدل را نشان میدهند.
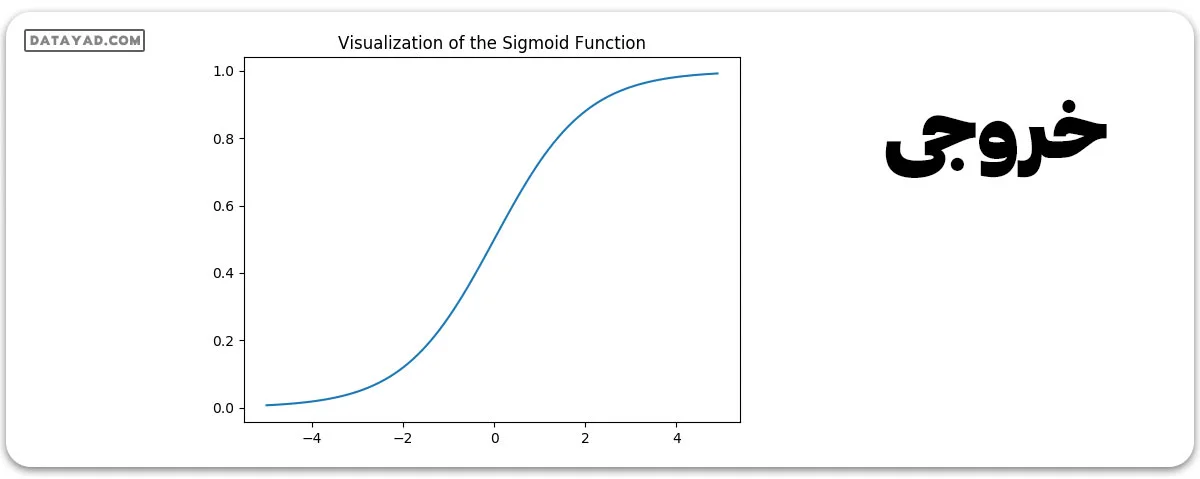
حالا بیایید نگاهی به نمودار تابع سیگموئید بیندازیم.
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(z):
return 1 / (1 + np.exp( - z))
plt.plot(np.arange(-5, 5, 0.1), sigmoid(np.arange(-5, 5, 0.1)))
plt.title('Visualization of the Sigmoid Function')
plt.show() توجه کنید که محدوده تابع سیگموئید بین (0, 1) است، به این معنی که مقادیر حاصل از آن بین 0 و 1 قرار دارند. این ویژگی تابع سیگموئید باعث میشود که این تابع به عنوان یک تابع فعالسازی، بسیار مناسب برای دستهبندی دوتایی باشد. همچنین برای z = 0، مقدار Sigmoid(z) برابر با 0.5 است که نقطه میانی محدوده تابع سیگموئید میباشد.
همانند رگرسیون خطی، ما نیاز داریم تا بهترین مقادیر برای w و b را پیدا کنیم که در آن تابع هزینه J کمینه باشد. در این مورد، از تابع هزینه “Sigmoid Cross Entropy” استفاده خواهیم کرد که به صورت زیر بیان میشود:
سپس این تابع هزینه با استفاده از روش گرادیان کاهشی بهینهسازی خواهد شد.
اجرا:
ابتدا با وارد کردن کتابخانههای لازم شروع میکنیم. برای محاسبات از کتابخانههای Numpy و Tensorflow، برای تحلیل دادههای اولیه از Pandas و برای نمودارکشی از Matplotlib استفاده خواهیم کرد. همچنین از ماژول پیشپردازش Scikit-Learn برای کدگذاری (One Hot Encoding) دادهها استفاده خواهیم کرد.
# importing modules import numpy as np import pandas as pd import tensorflow as tf import matplotlib.pyplot as plt from sklearn.preprocessing import OneHotEncoder
سپس، دیتاست را وارد خواهیم کرد. از یک زیرمجموعه از دیتاست معروف Iris استفاده خواهیم کرد.
data = pd.read_csv('dataset.csv', header = None)
print("Data Shape:", data.shape)
print(data.head()) خروجی:
Data Shape: (100, 4) 0 1 2 3 0 0 5.1 3.5 1 1 1 4.9 3.0 1 2 2 4.7 3.2 1 3 3 4.6 3.1 1 4 4 5.0 3.6 1
حالا بیایید ماتریس ویژگیها و برچسبهای مرتبط را دریافت کنیم و آنها را تصویر کنیم.
# Feature Matrix
x_orig = data.iloc[:, 1:-1].values
# Data labels
y_orig = data.iloc[:, -1:].values
print("Shape of Feature Matrix:", x_orig.shape)
print("Shape Label Vector:", y_orig.shape) خروجی:
Shape of Feature Matrix: (100, 2) Shape Label Vector: (100, 1)
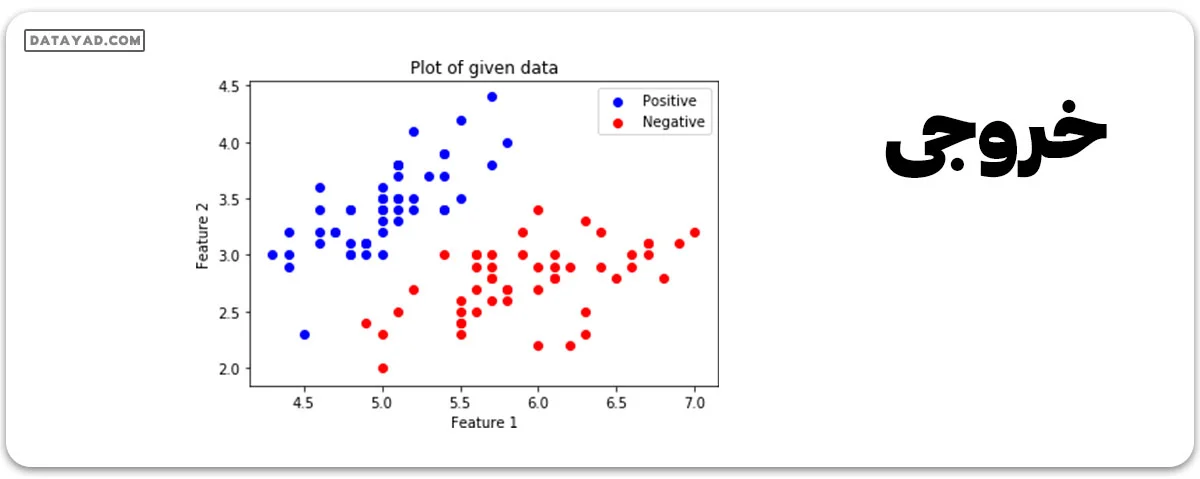
بصریسازی دیتا
# Positive Data Points
x_pos = np.array([x_orig[i] for i in range(len(x_orig))
if y_orig[i] == 1])
# Negative Data Points
x_neg = np.array([x_orig[i] for i in range(len(x_orig))
if y_orig[i] == 0])
# Plotting the Positive Data Points
plt.scatter(x_pos[:, 0], x_pos[:, 1], color = 'blue', label = 'Positive')
# Plotting the Negative Data Points
plt.scatter(x_neg[:, 0], x_neg[:, 1], color = 'red', label = 'Negative')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('Plot of given data')
plt.legend()
plt.show() اکنون ما دادهها را با استفاده از روش One Hot Encoding تبدیل خواهیم کرد تا با الگوریتم هماهنگ شود. کدگذاری واتهات ویژگیهای دستهای را به فرمتی تبدیل میکند که بهتر با الگوریتمهای دستهبندی و رگرسیون کار میکند. همچنین، ما نرخ یادگیری و تعداد دورهها (Epochs) را تنظیم خواهیم کرد.
# Creating the One Hot Encoder
oneHot = OneHotEncoder()
# Encoding x_orig
oneHot.fit(x_orig)
x = oneHot.transform(x_orig).toarray()
# Encoding y_orig
oneHot.fit(y_orig)
y = oneHot.transform(y_orig).toarray()
alpha, epochs = 0.0035, 500
m, n = x.shape
print('m =', m)
print('n =', n)
print('Learning Rate =', alpha)
print('Number of Epochs =', epochs) خروجی:
m = 100 n = 7 Learning Rate = 0.0035 Number of Epochs = 500
حالا شروع میکنیم به ساختن مدل با تعریف پلیسهولدرهای (placeholders) X و Y. این کار به ما این امکان را میدهد که نمونههای آموزشی x و y را در طول فرایند آموزش به سیستم وارد کنیم. همچنین، ما به ساخت متغیرهای قابل یادگیری W و b میپردازیم که قابل بهینهسازی توسط روش گرادیان کاهشی هستند.
# There are n columns in the feature matrix # after One Hot Encoding. X = tf.placeholder(tf.float32, [None, n]) # Since this is a binary classification problem, # Y can take only 2 values. Y = tf.placeholder(tf.float32, [None, 2]) # Trainable Variable Weights W = tf.Variable(tf.zeros([n, 2])) # Trainable Variable Bias b = tf.Variable(tf.zeros([2]))
در مرحله بعد، فرضیه، تابع هزینه، بهینهساز و اولیهسازی متغیرهای global را تعریف میکنیم.
# Hypothesis Y_hat = tf.nn.sigmoid(tf.add(tf.matmul(X, W), b)) # Sigmoid Cross Entropy Cost Function cost = tf.nn.sigmoid_cross_entropy_with_logits( logits = Y_hat, labels = Y) # Gradient Descent Optimizer optimizer = tf.train.GradientDescentOptimizer( learning_rate = alpha).minimize(cost) # Global Variables Initializer init = tf.global_variables_initializer()
فرایند آموزش را درون یک TensorFlow Sessionشروع کنید.
# Starting the Tensorflow Session
with tf.Session() as sess:
# Initializing the Variables
sess.run(init)
# Lists for storing the changing Cost and Accuracy in every Epoch
cost_history, accuracy_history = [], []
# Iterating through all the epochs
for epoch in range(epochs):
cost_per_epoch = 0
# Running the Optimizer
sess.run(optimizer, feed_dict = {X : x, Y : y})
# Calculating cost on current Epoch
c = sess.run(cost, feed_dict = {X : x, Y : y})
# Calculating accuracy on current Epoch
correct_prediction = tf.equal(tf.argmax(Y_hat, 1),
tf.argmax(Y, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction,
tf.float32))
# Storing Cost and Accuracy to the history
cost_history.append(sum(sum(c)))
accuracy_history.append(accuracy.eval({X : x, Y : y}) * 100)
# Displaying result on current Epoch
if epoch % 100 == 0 and epoch != 0:
print("Epoch " + str(epoch) + " Cost: "
+ str(cost_history[-1]))
Weight = sess.run(W) # Optimized Weight
Bias = sess.run(b) # Optimized Bias
# Final Accuracy
correct_prediction = tf.equal(tf.argmax(Y_hat, 1),
tf.argmax(Y, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction,
tf.float32))
print("\nAccuracy:", accuracy_history[-1], "%") خروجی:
Epoch 100 Cost: 125.700202942 Epoch 200 Cost: 120.647117615 Epoch 300 Cost: 118.151592255 Epoch 400 Cost: 116.549999237 Accuracy: 91.0000026226 %
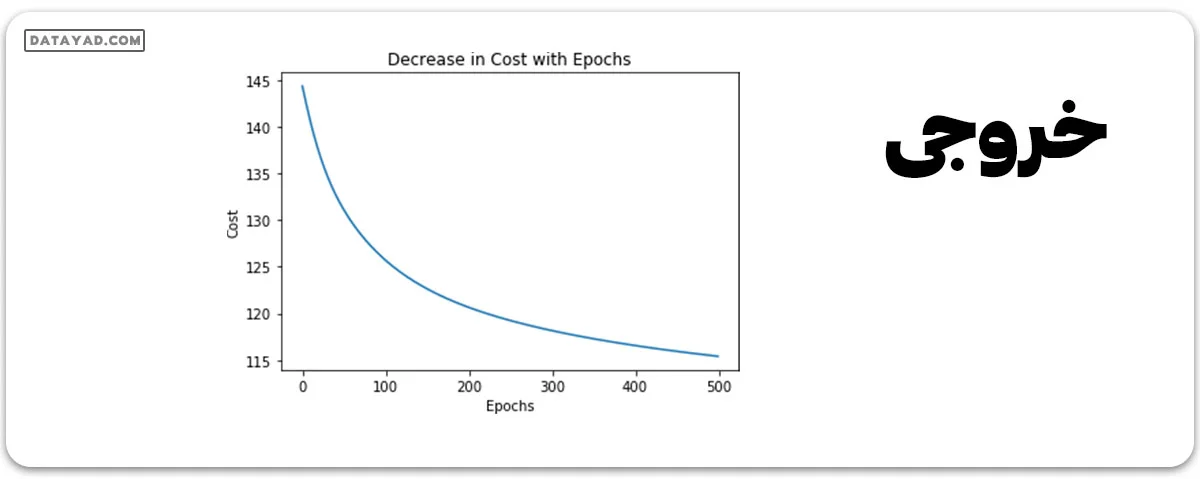
بیایید تغییرات هزینه را در طول دورهها (Epochs) پلات کنیم.
plt.plot(list(range(epochs)), cost_history)
plt.xlabel('Epochs')
plt.ylabel('Cost')
plt.title('Decrease in Cost with Epochs')
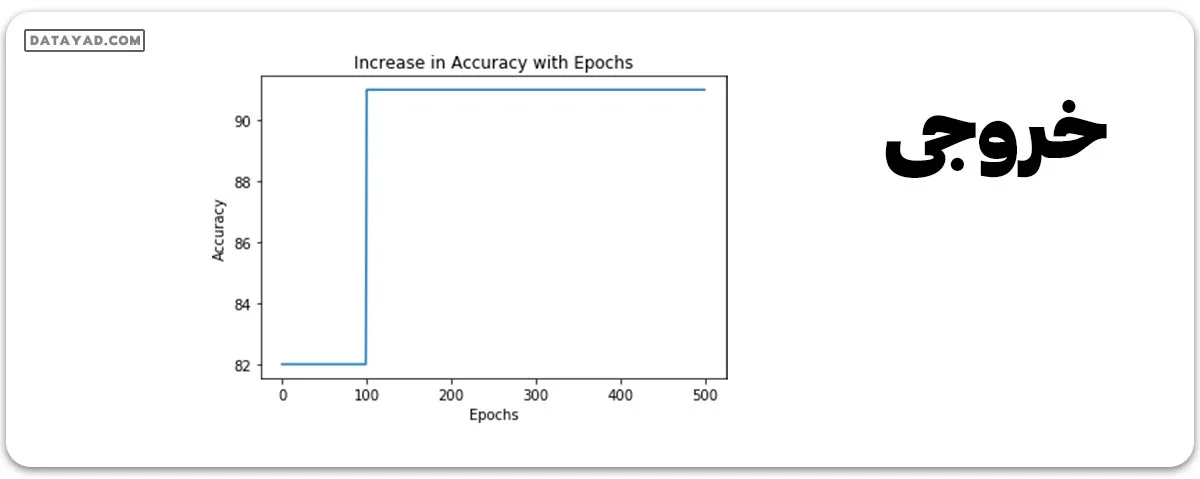
plt.show() تغییرات دقت را در طول دورهها (Epochs) به صورت نموداری نشان دهید.
plt.plot(list(range(epochs)), accuracy_history)
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.title('Increase in Accuracy with Epochs')
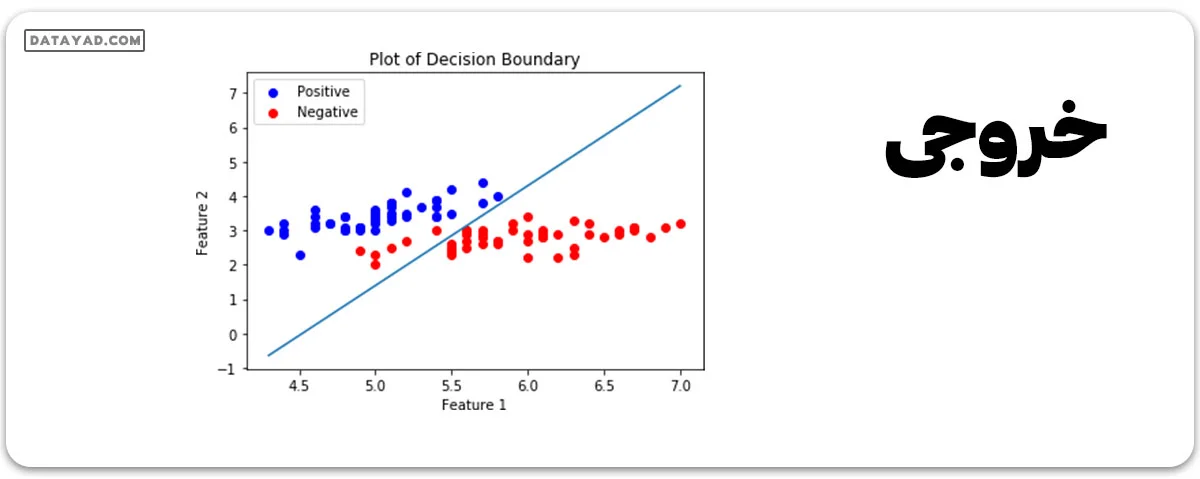
plt.show() اکنون ما مرز تصمیمگیری برای کلاسیفایر آموزش دیده خود را رسم خواهیم کرد. مرز تصمیمگیری یک سطح فراگیر است که فضای برداری زیرین را به دو بخش تقسیم میکند، یک بخش برای هر کلاس.
# Calculating the Decision Boundary
decision_boundary_x = np.array([np.min(x_orig[:, 0]),
np.max(x_orig[:, 0])])
decision_boundary_y = (- 1.0 / Weight[0]) *
(decision_boundary_x * Weight + Bias)
decision_boundary_y = [sum(decision_boundary_y[:, 0]),
sum(decision_boundary_y[:, 1])]
# Positive Data Points
x_pos = np.array([x_orig[i] for i in range(len(x_orig))
if y_orig[i] == 1])
# Negative Data Points
x_neg = np.array([x_orig[i] for i in range(len(x_orig))
if y_orig[i] == 0])
# Plotting the Positive Data Points
plt.scatter(x_pos[:, 0], x_pos[:, 1],
color = 'blue', label = 'Positive')
# Plotting the Negative Data Points
plt.scatter(x_neg[:, 0], x_neg[:, 1],
color = 'red', label = 'Negative')
# Plotting the Decision Boundary
plt.plot(decision_boundary_x, decision_boundary_y)
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('Plot of Decision Boundary')
plt.legend()
plt.show()