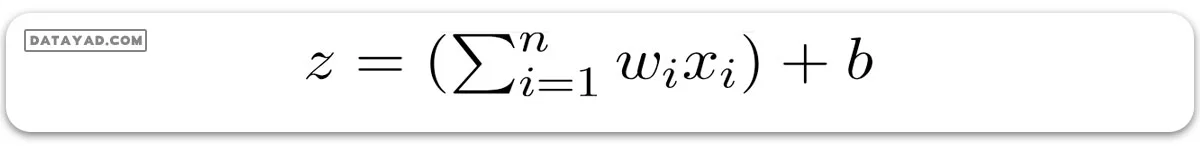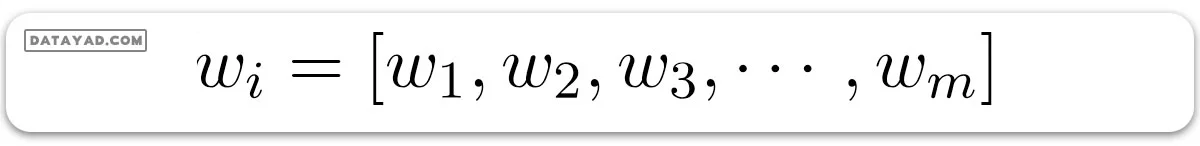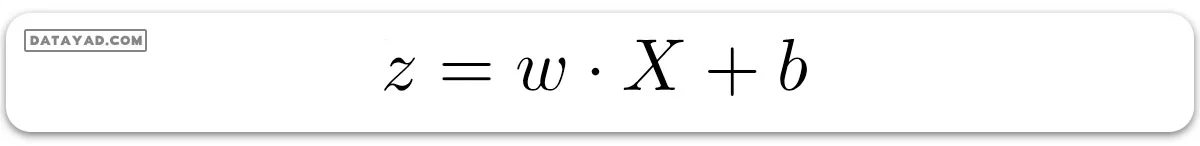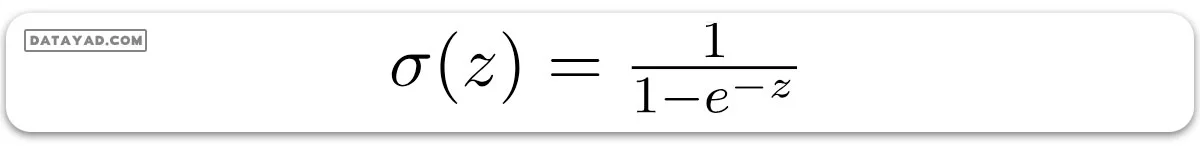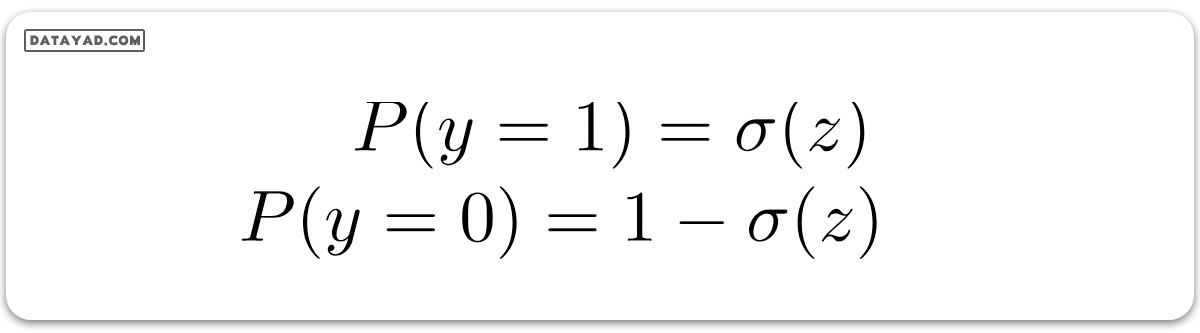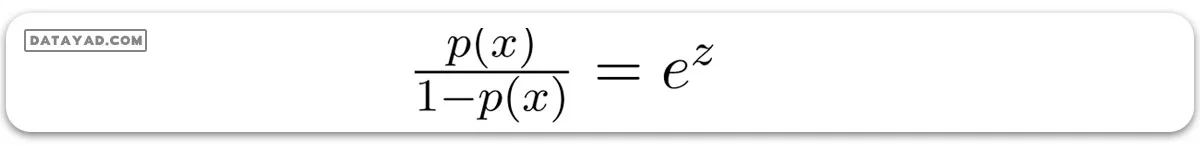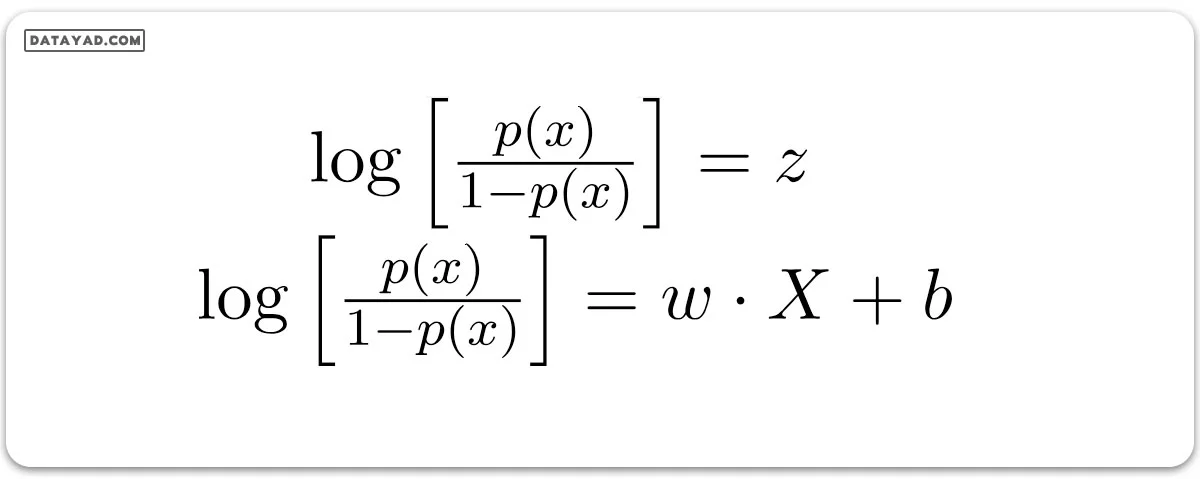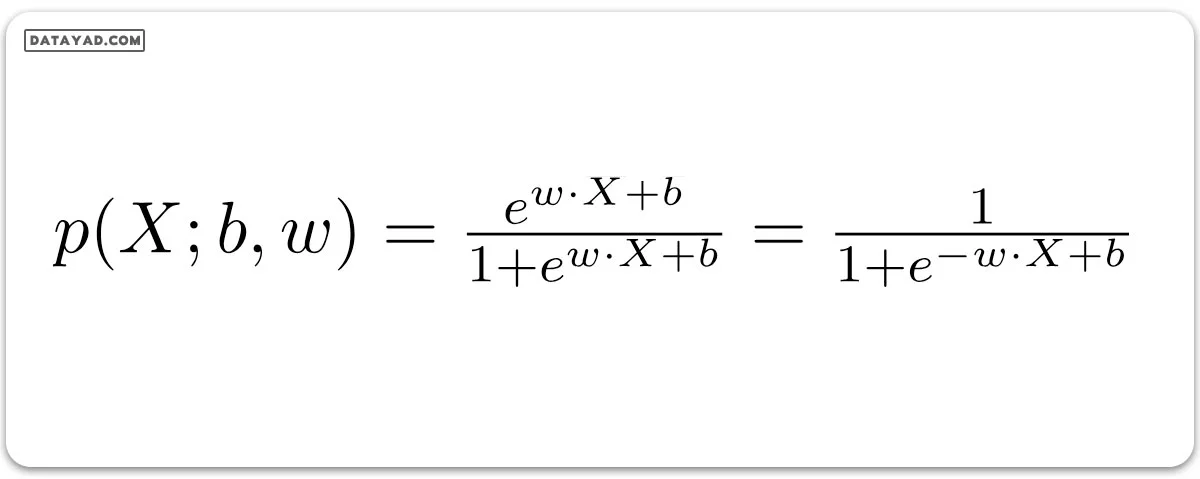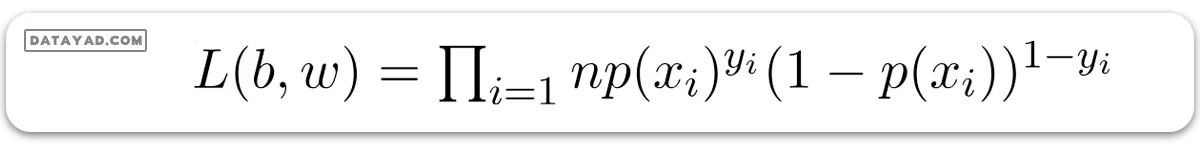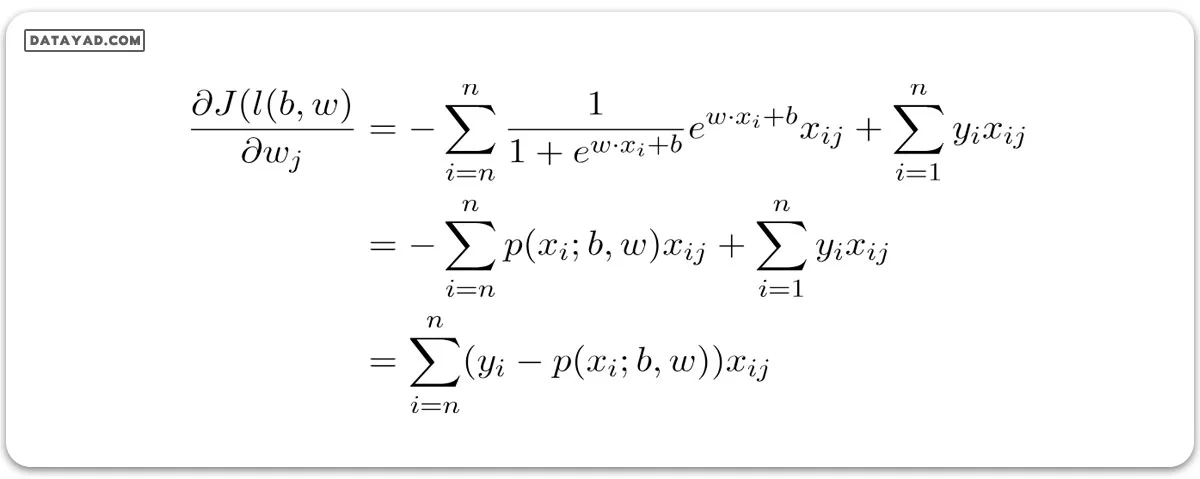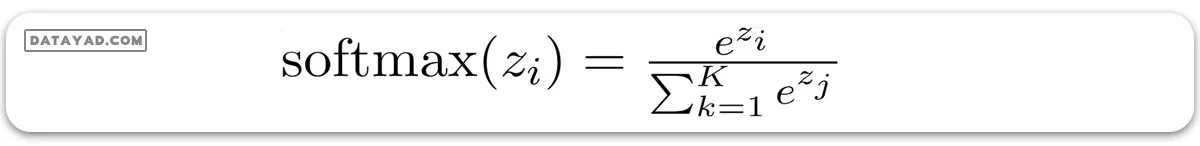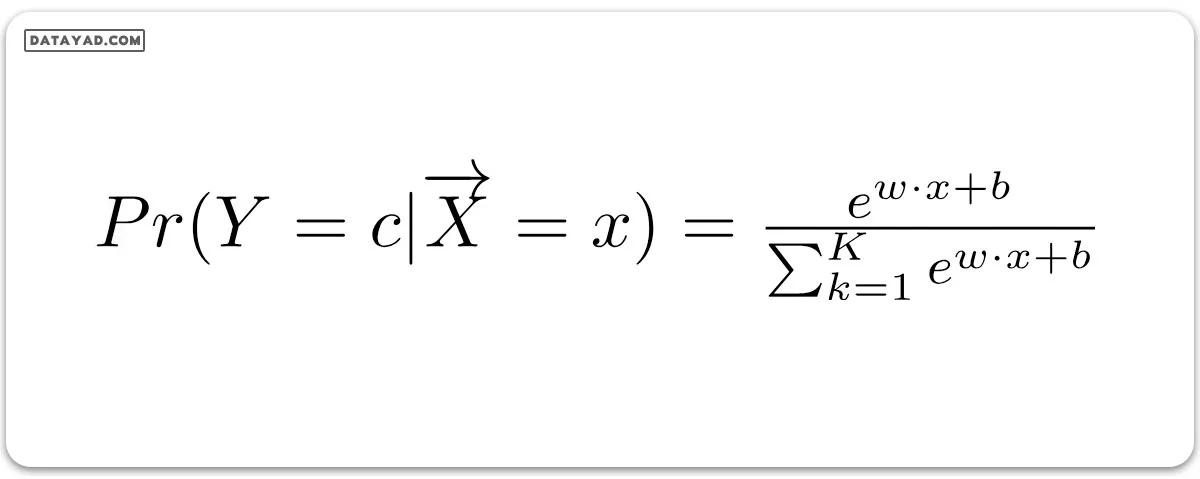رگرسیون لجستیک در یادگیری ماشین

رگرسیون لجستیک، یک الگوریتم یادگیری ماشین با نظارت است که بیشتر برای طبقه‌بندی استفاده می‌شود. هدف این است که احتمال وابستگی یک داده به یک کلاس خاص را پیش‌بینی کند. این الگوریتم، که جنبه‌های آماری دارد، به بررسی ارتباط بین متغیرهای مستقل و متغیرهای وابسته دودویی می‌پردازد. این الگوریتم یک ابزار قدرتمند برای تصمیم‌گیری است، مثل تشخیص اینکه آیا یک ایمیل اسپم است یا خیر.

این الگوریتم‌ برای طبقه‌بندی به کار می‌رود و به نام رگرسیون لجستیک شناخته می‌شود. علت نامگذاری آن به رگرسیون این است که خروجی تابع رگرسیون خطی را به عنوان ورودی می‌گیرد ولی از تابع سیگموئید (sigmoid) برای برآورد احتمال وابستگی به کلاس داده شده استفاده می‌کند. تفاوت بین رگرسیون خطی و رگرسیون لجستیک این است که خروجی رگرسیون خطی یک مقدار پیوسته است که می‌تواند هر چیزی باشد، در حالی که رگرسیون لجستیک احتمال وابستگی یک نمونه به کلاس مشخص یا عدم وابستگی به آن را پیش‌بینی می‌کند.

رگرسیون لجستیک در یادگیری ماشین

این روش برای پیش‌بینی وضعیت متغیر وابسته‌ی دسته‌ای با استفاده از مجموعه‌ای از متغیرهای مستقل به کار می‌رود.

✅ رگرسیون لجستیک (Logistic Regression)، خروجی یک متغیر وابسته‌ی دسته‌ای را پیش‌بینی می‌کند. بنابراین، نتیجه باید یک مقدار دسته‌ای یا گسسته باشد.

✅ خروجی آن می‌تواند بله یا خیر، ۰ یا ۱، درست یا غلط و موارد مشابه باشد. اما به جای دادن مقدار دقیق به صورت ۰ و ۱، مقادیری احتمالی، که بین ۰ و ۱ قرار دارند را، ارائه می‌دهد.

✅ رگرسیون لجستیک بسیار شبیه به رگرسیون خطی است، به جز نحوه‌ی استفاده از آنها. رگرسیون خطی برای حل مسائل رگرسیونی به کار می‌رود، در حالی که رگرسیون لجستیک برای حل مسائل طبقه‌بندی استفاده می‌شود.

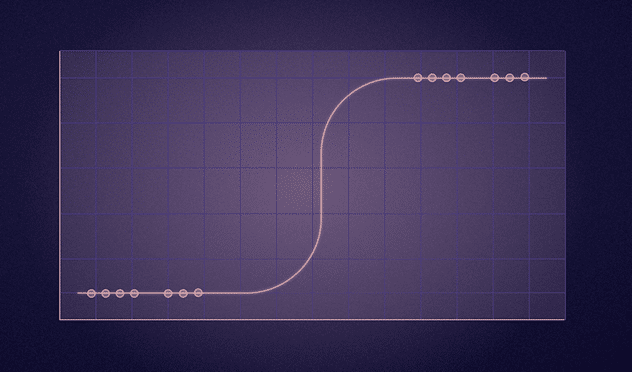
✅ در رگرسیون لجستیک، به جای انطباق یک خط رگرسیون، یک تابع لجستیک به شکل “S” را انطباق می‌دهیم که دو مقدار حداکثری (۰ یا ۱) را پیش‌بینی می‌کند.

✅ منحنی حاصل از تابع لجستیک احتمال وقوع چیزی مانند اینکه آیا سلول‌ها سرطانی هستند یا نه، آیا یک موش بر اساس وزنش چاق است یا نه و غیره را نشان می‌دهد.

✅ رگرسیون لجستیک یک الگوریتم مهم یادگیری ماشین است زیرا قادر است احتمالات را ارائه دهد و داده‌های جدید را با استفاده از مجموعه‌های داده‌ی پیوسته و گسسته طبقه‌بندی کند.

✅ رگرسیون لجستیک می‌تواند برای طبقه‌بندی مشاهدات با استفاده از انواع مختلف داده‌ها به کار رود و به راحتی موثرترین متغیرها را برای طبقه‌بندی تعیین کند.

تابع لجستیک (تابع سیگموئید)

✅ تابع سیگموئید (sigmoid) یک تابع ریاضی است که برای نگاشتن مقادیر پیش‌بینی شده به احتمالات به کار می‌رود.

✅ این تابع هر مقدار واقعی را به مقدار دیگری در بازه‌ی ۰ تا ۱ نگاشت می‌کند. مقدار رگرسیون لجستیک باید بین ۰ و ۱ باشد و نمی‌تواند از این حد فراتر رود، بنابراین یک منحنی به شکل “S” را تشکیل می‌دهد.

✅ این منحنی به شکل S به تابع سیگموئید یا تابع لجستیک معروف است.

✅ در رگرسیون لجستیک، ما از مفهوم مقدار آستانه استفاده می‌کنیم که احتمال ۰ یا ۱ را تعریف می‌کند. به عنوان مثال، مقادیری که بالاتر از مقدار آستانه هستند معمولاً ۱ هستند و مقادیری که زیر مقدار آستانه قرار دارند معمولاً ۰ هستند.

انواع رگرسیون لجستیک

بر اساس دسته‌بندی‌ها، رگرسیون لجستیک را می‌توان به سه نوع تقسیم کرد:

۱. دودویی (Binomial)

در رگرسیون لجستیک دودویی، تنها دو نوع ممکن برای متغیر وابسته وجود دارد، مانند ۰ یا ۱، قبولی یا ردی و غیره.

۲. چندمتغیره (Multinomial)

در رگرسیون لجستیک چندمتغیره، سه یا بیشتر نوع ممکن غیرمرتب برای متغیر وابسته وجود دارد، مانند “گربه”، “سگ” یا “گوسفند”.

۳. ترتیبی (Ordinal)

در رگرسیون لجستیک ترتیبی، سه یا بیشتر نوع ممکن مرتب برای متغیر وابسته وجود دارد، مانند “کم”، “متوسط” یا “زیاد”.

مقایسه رگرسیون خطی و رگرسیون لجستیک

 مفاهیم مرتبط با رگرسیون لجستیک

در اینجا برخی از اصطلاحات رایج مرتبط با رگرسیون لجستیک آورده شده است:

– متغیرهای مستقل: ویژگی‌های ورودی یا عوامل پیش‌بینی‌کننده‌ای که برای پیش‌بینی‌های متغیر وابسته به کار می‌روند.

– متغیر وابسته: متغیر هدف در مدل رگرسیون لجستیک که تلاش داریم آن را پیش‌بینی کنیم.

– تابع لجستیک: فرمولی که استفاده می‌شود تا نشان دهد چگونه متغیرهای مستقل و وابسته با یکدیگر ارتباط دارند. تابع لجستیک متغیرهای ورودی را به یک مقدار احتمال بین ۰ تا ۱ تبدیل می‌کند که احتمال اینکه متغیر وابسته ۱ یا ۰ باشد را نشان می‌دهد.

– شانس یا احتمال موفقیت (odds): نسبت وقوع یک رخداد به عدم وقوع آن است. این مفهوم با احتمال متفاوت است زیرا احتمال، نسبت وقوع یک رخداد به همه چیزهایی است که ممکن است رخ دهند.

– لگاریتم موفقیت (لگاریتم شانس): لگاریتم موفقیت که به عنوان تابع لوجیت نیز شناخته می‌شود، لگاریتم طبیعی موفقیت است. در رگرسیون لجستیک، لگاریتم موفقیت متغیر وابسته به عنوان یک ترکیب خطی از متغیرهای مستقل و عرض از مبداء مدل‌سازی می‌شود.

– ضریب: پارامترهای تخمین زده شده مدل رگرسیون لجستیک، نشان می‌دهند که چگونه متغیرهای مستقل و وابسته به یکدیگر مرتبط هستند.

– عرض از مبدا (intercept): یک عبارت ثابت در مدل رگرسیون لجستیک که لگاریتم احتمالات را زمانی که همه متغیرهای مستقل برابر با صفر هستند، نشان می‌دهد.

– برآورد حداکثر احتمال: روشی که برای تخمین ضرایب مدل رگرسیون لجستیک استفاده می‌شود، که احتمال مشاهده داده‌ها را با توجه به مدل به حداکثر می‌رساند.

رگرسیون لجستیک چگونه کار می‌کند؟

مدل رگرسیون لجستیک، خروجی های مقدار پیوسته تابع رگرسیون خطی را با استفاده از تابع سیگموئید به خروجی‌های دسته‌ای تبدیل می‌کند. این تابع توانایی نگاشت هر مجموعه‌ای از متغیرهای مستقل به یک مقدار بین صفر و یک را دارد و به نام تابع لجستیک شناخته می‌شود.

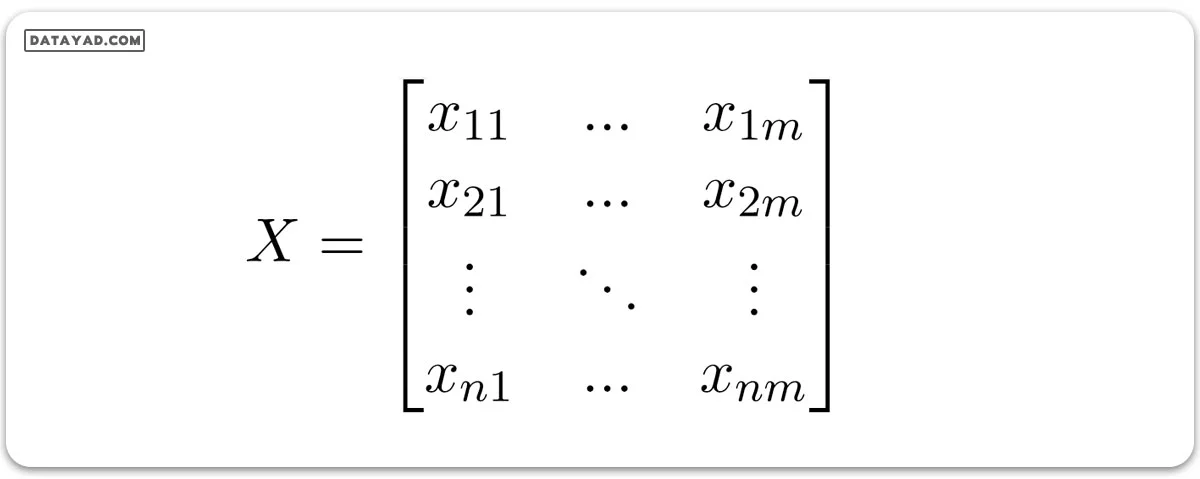
بیایید فرض کنیم ورودی‌های مستقل به صورت زیر باشند:

و متغیر وابسته Y فقط مقادیر دو حالتی یعنی صفر یا یک دارد:

سپس یک تابع خطی چندگانه را به متغیرهای ورودیX  اعمال می‌کنیم:

در اینجا x با اندیس i نمونه iام از X است. و w در تصویر زیر وزن‌ها یا ضرایب هستند.

و مقدار b در واقع ترم بایاس است که به عنوان عرض از مبدا نیز شناخته می‌شود. پیش‌بینی خطی مدل قبل از اعمال تابع سیگموئید به سادگی می‌تواند به صورت حاصل‌ضرب نقطه‌ای وزن و بایاس، یعنی به شکل زیر بیان شود:

آنچه که تا به حال بحث کردیم، رگرسیون خطی بود.

تابع سیگموئید

حال ما از تابع سیگموئید (sigmoid) استفاده می‌کنیم که در آن ورودی z خواهد بود و ما احتمال را بین 0 و 1 پیدا می‌کنیم، یعنی y پیش‌بینی شده.

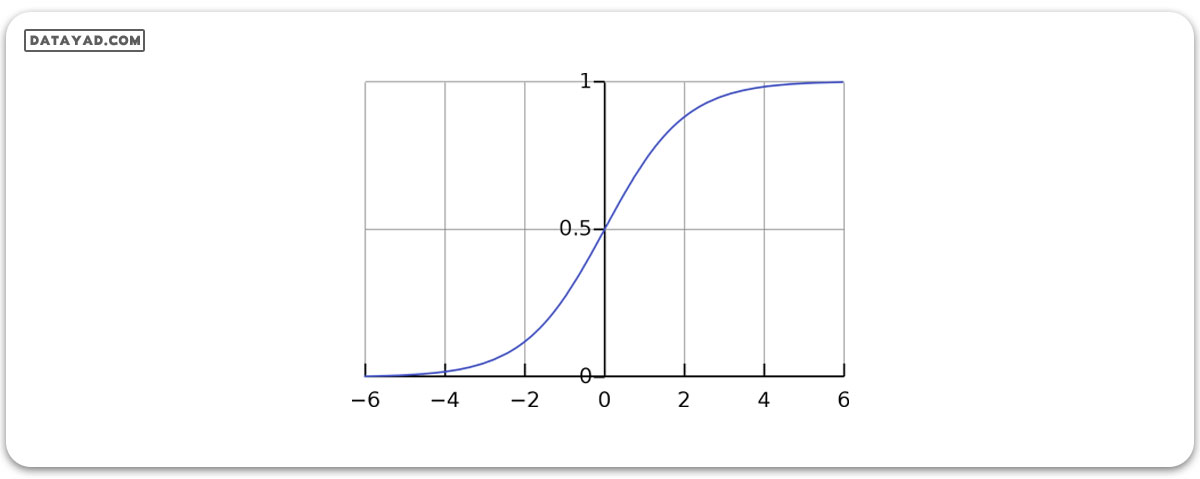
نمودار تابع سیگموئید مانند تصویر زیر است.

همانطور که در بالا نشان داده شده است، تابع سیگموئید داده‌های متغیر پیوسته را به احتمال تبدیل می‌کند، یعنی بین 0 و 1.

– هنگامی که ورودی به سمت مثبت بی نهایت میل می کند، خروجی سیگما به سمت یک میل می‌کند.

– هنگامی که ورودی به سمت منفی بی نهایت میل می کند خروجی سیگما به سمت صفر میل می‌کند.

پس خروجی این تابع همیشه بین 0 و 1 است.

احتمال وابستگی به یک کلاس می‌تواند به صورت زیر اندازه‌گیری شود:

معادله رگرسیون لجستیک

شانس (odd) نشان‌دهنده نسبت احتمال وقوع یک رخداد به احتمال عدم وقوع آن است که متفاوت از احتمال مطلق است. در رگرسیون لجستیک، شانس به صورت زیر محاسبه می‌شود:

زمانی که ما لگاریتم طبیعی این شانس را حساب می‌کنیم، خروجی به این شکل در می‌آید:

با این حساب، معادله نهایی رگرسیون لجستیک که احتمال p(X) را نشان می‌دهد، به این شکل است:

تابع احتمال برای رگرسیون لجستیک

احتمالات پیش‌بینی شده برایy=1  به این شکل p(X; b, w) = p(x) خواهد بود.

و تابع احتمال L(b, w) به صورت زیر تعریف می‌شود:

با گرفتن لگاریتم طبیعی از هر دو طرف، ما به معادله لگاریتم احتمال می‌رسیم:

برای یافتن برآوردهای حداکثر احتمال (maximum likelihood)، نسبت به w مشتق می‌گیریم.

فرضیات رگرسیون لجستیک

– مشاهدات مستقل: هر مشاهده‌ای از دیگری مستقل است، به این معنا که بین هیچ یک از متغیرهای ورودی همبستگی وجود ندارد.

– متغیرهای وابسته دودویی: این فرض بر این است که متغیر وابسته باید دودویی یا دو حالتی باشد، به این معنی که فقط می‌تواند دو مقدار بگیرد. برای بیش از دو دسته، از توابع سافتمکس استفاده می‌شود.

– رابطه خطی بین متغیرهای مستقل و لگ شانس: رابطه بین متغیرهای مستقل و لگ شانس متغیر وابسته باید خطی باشد.

– بدون وجود ناهنجاری‌ها (outliers): در مجموعه داده نباید ناهنجاری‌ وجود داشته باشد.

– اندازه نمونه بزرگ: اندازه نمونه باید به اندازه کافی بزرگ باشد.

انواع رگرسیون لجستیک

بر اساس تعداد دسته‌ها، رگرسیون لجستیک می‌تواند به صورت زیر طبقه‌بندی شود:

رگرسیون لجستیک دودویی

متغیر هدف فقط می‌تواند دو نوع ممکن داشته باشد: “۰” یا “۱” که می‌تواند نشان‌دهنده “برد” در مقابل “باخت”، “قبولی” در مقابل “ردی”، “مرده” در مقابل “زنده” و غیره باشد. در این حالت، از توابع سیگموئید استفاده می‌شود که قبلاً بحث شده است.

# import the necessary libraries
from sklearn.datasets import load_breast_cancer
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# load the breast cancer dataset
X, y = load_breast_cancer(return_X_y=True)
# split the train and test dataset
X_train, X_test,\
	y_train, y_test = train_test_split(X, y,
									test_size=0.20,
									random_state=23)
# LogisticRegression
clf = LogisticRegression(random_state=0)
clf.fit(X_train, y_train)
# Prediction
y_pred = clf.predict(X_test)

acc = accuracy_score(y_test, y_pred)
print("Logistic Regression model accuracy (in %):", acc*100)

خروجی:

Logistic Regression model accuracy (in %): 95.6140350877193

رگرسیون لجستیک چندمتغیره

متغیر هدف می‌تواند سه یا بیشتر نوع ممکن داشته باشد که مرتب نیستند (یعنی دسته‌ها اهمیت کمیت ندارند) مانند “بیماری A” در مقابل “بیماری B” در مقابل “بیماری C“.

در این حالت، به جای تابع سیگموئید، از تابع سافتمکس (softmax) استفاده می‌شود. تابع سافتمکس برای K کلاس به صورت زیر خواهد بود:

پس احتمال به صورت زیر خواهد بود:

در رگرسیون لجستیک چندمتغیره، متغیر خروجی می‌تواند بیش از دو خروجی گسسته ممکن داشته باشد. به عنوان مثال، داده‌های اعداد را در نظر بگیرید.

from sklearn.model_selection import train_test_split
from sklearn import datasets, linear_model, metrics

# load the digit dataset
digits = datasets.load_digits()

# defining feature matrix(X) and response vector(y)
X = digits.data
y = digits.target

# splitting X and y into training and testing sets
X_train, X_test,\
	y_train, y_test = train_test_split(X, y,
									test_size=0.4,
									random_state=1)

# create logistic regression object
reg = linear_model.LogisticRegression()

# train the model using the training sets
reg.fit(X_train, y_train)

# making predictions on the testing set
y_pred = reg.predict(X_test)

# comparing actual response values (y_test)
# with predicted response values (y_pred)
print("Logistic Regression model accuracy(in %):",
	metrics.accuracy_score(y_test, y_pred)*100)

خروجی:

Logistic Regression model accuracy(in %): 96.52294853963839

رگرسیون لجستیک ترتیبی

این نوع با متغیرهای هدفی که دارای دسته‌های مرتب هستند سروکار دارد. به عنوان مثال، نمره یک آزمون می‌تواند به عنوان “خیلی ضعیف”، “ضعیف”، “خوب” یا “خیلی خوب” دسته‌بندی شود. در اینجا، به هر دسته می‌توان امتیازی مانند ۰، ۱، ۲ یا ۳ داد.

مراحل اعمال مدل‌سازی رگرسیون لجستیک

مراحل زیر در مدل‌سازی رگرسیون لجستیک دخیل هستند:

– تعریف مسئله: شناسایی متغیر وابسته و متغیرهای مستقل و تعیین اینکه آیا مسئله یک مسئله طبقه‌بندی دودویی است یا خیر.

– آماده‌سازی داده‌ها: پاک‌سازی و پیش‌پردازش داده‌ها و اطمینان از اینکه داده‌ها برای مدل‌سازی رگرسیون لجستیک مناسب هستند.

– تحلیل اکتشافی داده‌ها (EDA): تصویرسازی روابط بین متغیرهای وابسته و مستقل و شناسایی هرگونه ناهنجاری یا خطا در داده‌ها.

– انتخاب ویژگی‌ها: انتخاب متغیرهای مستقلی که رابطه مهمی با متغیر وابسته دارند و حذف ویژگی‌های اضافی یا نامربوط.

– ساخت مدل: آموزش مدل رگرسیون لجستیک بر روی متغیرهای مستقل انتخاب شده و تخمین ضرایب مدل.

– ارزیابی مدل: ارزیابی عملکرد مدل رگرسیون لجستیک با استفاده از معیارهای مناسب مانند دقت، دقت پیش‌بینی، بازیابی، نمره F1 یا AUC-ROC.

– بهبود مدل: بر اساس نتایج ارزیابی، تنظیم مجدد مدل با تغییر متغیرهای مستقل، افزودن ویژگی‌های جدید یا استفاده از تکنیک‌های تنظیم‌سازی برای کاهش بیش‌برازش.

– استقرار مدل: به کارگیری مدل رگرسیون لجستیک در یک سناریوی واقعی و پیش‌بینی روی داده‌های جدید.

تنظیم آستانه در مدل رگرسیون لجستیک

رگرسیون لجستیک تنها زمانی به یک تکنیک طبقه‌بندی تبدیل می‌شود که یک آستانه تصمیم‌گیری در نظر گرفته شود. تنظیم مقدار آستانه جنبه بسیار مهمی از رگرسیون لجستیک است و به خود مسئله طبقه‌بندی بستگی دارد.

تصمیم برای مقدار آستانه بیشتر تحت تأثیر مقادیر دقت (Precision) و بازیابی (Recall) قرار دارد. در حالت ایده‌آل، ما می‌خواهیم هم دقت و هم بازیابی ۱ باشند، اما این معمولاً اتفاق نمی‌افتد.

در مواردی که باید بین بهینگی دقت و بازیابی یکی را انتخاب کنیم، از استدلال‌های زیر برای تصمیم‌گیری درباره آستانه استفاده می‌کنیم:

✅ دقت کم/بازیابی بالا: در کاربردهایی که می‌خواهیم تعداد نادرست‌های منفی را بدون لزوم کاهش تعداد نادرست‌های مثبت کاهش دهیم، یک مقدار تصمیم‌گیری را انتخاب می‌کنیم که دارای مقدار کمی از دقت یا مقدار بالایی از بازیابی باشد.

به عنوان مثال، در یک برنامه تشخیص سرطان، ما نمی‌خواهیم هیچ بیمار مبتلا به عنوان سالم طبقه‌بندی شود، بدون اینکه توجه زیادی به این داشته باشیم که فرد سالم به اشتباه سرطانی تشخیص داده شده باشد.

این به این دلیل است که عدم وجود سرطان می‌تواند با آزمایش های پزشکی بیشتر، تشخیص داده شود اما وجود بیماری در یک کاندیدا که قبلاً به عنوان سالم طبقه بندی شده است، ممکن نیست.

✅ دقت بالا/بازیابی کم: در کاربردهایی که می‌خواهیم تعداد نادرست‌های مثبت را بدون لزوم کاهش تعداد نادرست‌های منفی کاهش دهیم، در این حالت مقدار تصمیم‌گیری را انتخاب می‌کنیم که دارای مقدار بالایی از دقت یا مقدار کمی از بازیابی باشد.

به عنوان مثال، اگر مشتریان را بر اساس واکنش مثبت یا منفی به تبلیغات طبقه‌بندی می‌کنیم، می‌خواهیم کاملاً مطمئن باشیم که مشتری به تبلیغ واکنش مثبت نشان می‌دهد.

زیرا در غیر این صورت، یک واکنش منفی می‌تواند منجر به از دست دادن فروش بالقوه به آن مشتری شود.