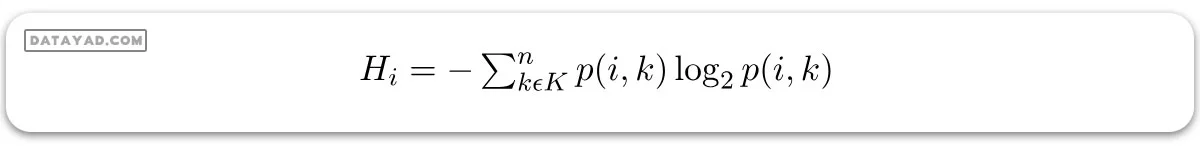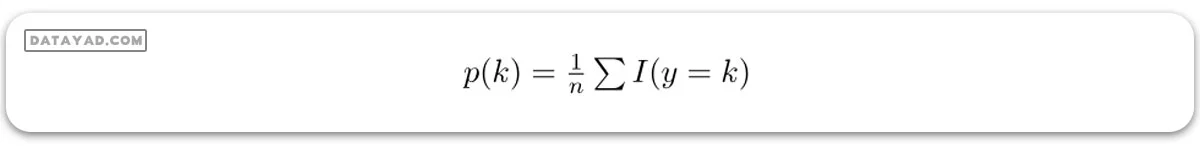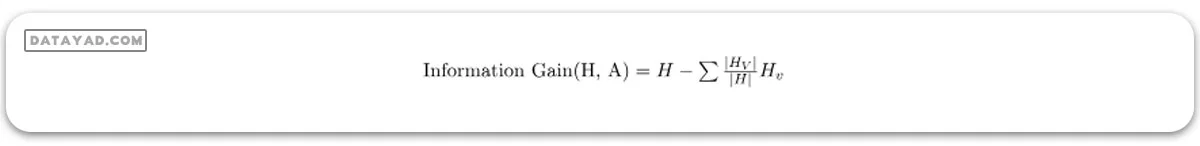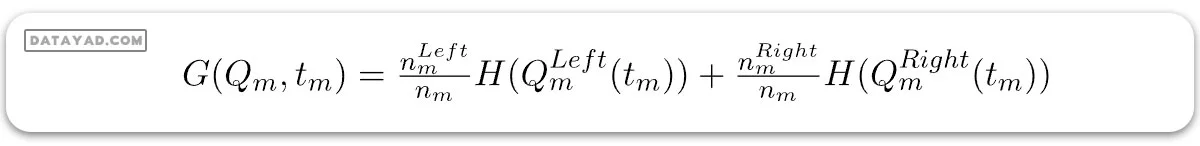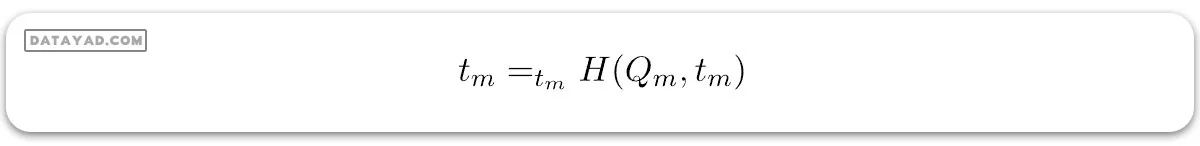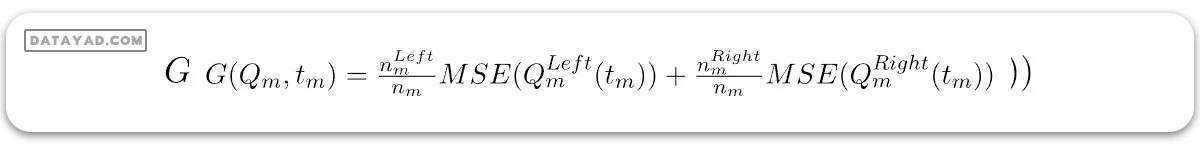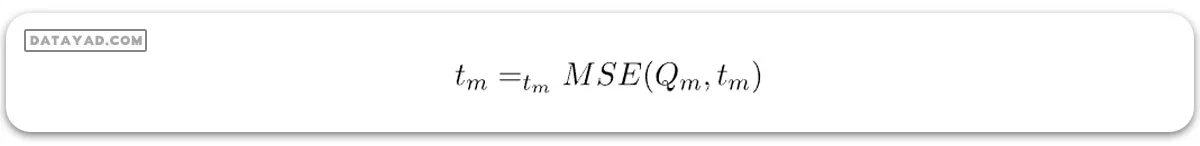درخت تصمیم (Decision Tree) چیست؟

بفرست برای دوستت

درخت تصمیم یکی از قدرتمندترین ابزارهای الگوریتم‌های یادگیری ماشین تحت نظارت است که برای وظایف دسته‌بندی و رگرسیون استفاده می‌شود. این درخت یک ساختار درختی شبیه به یک نمودار جریان ایجاد می‌کند که در هر گره داخلی یک آزمون بر یک ویژگی انجام می‌دهد، هر شاخه نتیجه آزمون را نمایان می‌سازد و هر گره برگ (گره نهایی) یک برچسب کلاس را نگه می‌دارد. این درخت با تقسیم داده‌های آموزشی به زیرمجموعه‌ها به صورت بازگشتی، بر اساس ارزیابی ویژگی‌ها ساخته می‌شود تا یک شرط توقف برآورده شود، مانند حداکثر عمق درخت یا حداقل تعداد نمونه‌های مورد نیاز برای تقسیم یک گره.

در حین آموزش، الگوریتم درخت تصمیم بهترین ویژگی را برای تقسیم داده‌ها انتخاب می‌کند بر اساس معیاری مانند آنتروپی یا ناخالصی Gini که میزان عدم قطعیت یا پیچیدگی در زیرمجموعه‌ها را اندازه‌گیری می‌کنند. هدف این است که ویژگی را پیدا کند که بیشترین بهره‌وری اطلاعات یا کاهش عدم قطعیت پس از تقسیم را بیشینه کند.

درخت تصمیم چیست؟

درخت تصمیم (Decision Tree) یک ساختار درختی، مانند نمودار جریان است که در آن هر گره داخلی یک ویژگی را نمایان می‌کند، شاخه‌ها قوانین را نشان می‌دهند و گره‌های برگ نتیجه الگوریتم را نشان می‌دهند. این الگوریتم یک الگوریتم یادگیری ماشین تحت نظارت است که برای حل مسائل دسته‌بندی و رگرسیون از آن استفاده می‌شود. این الگوریتم یکی از الگوریتم‌های بسیار قدرتمند است و همچنین در جنگل تصادفی (Random Forest) برای آموزش روی زیرمجموعه‌های مختلف از داده‌های آموزشی استفاده می‌شود. این الگوریتم به تنهایی یکی از الگوریتم‌های برجسته در یادگیری ماشین محسوب می‌شود.

اصطلاحات درخت تصمیم

بعضی از اصطلاحات متداول مورد استفاده در درخت تصمیم عبارتند از:

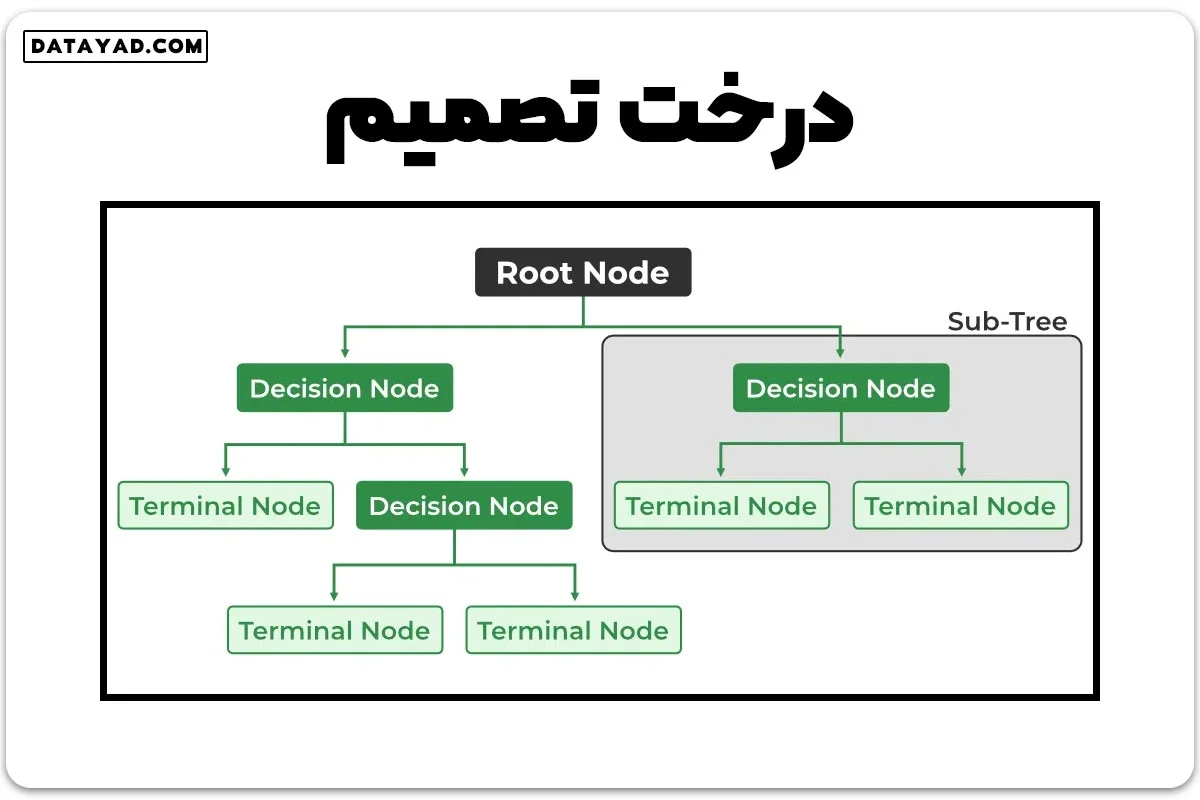
– ریشه (Root Node): بالاترین گره درخت که داده کلی را نمایان می‌کند. این نقطه شروع فرآیند تصمیم‌گیری است.

– تصمیم/گره داخلی (Decision/Internal Node): گره‌ای که یک انتخاب درباره یک ویژگی ورودی نمایان می‌کند. از گره‌های داخلی شاخه‌ها به گره‌های برگ یا گره‌های داخلی دیگر متصل می‌شود.

– برگ/گره نهایی (Leaf/Terminal Node): گره‌ای که هیچ گره فرزندی ندارد و یک برچسب کلاس یا یک مقدار عددی را نمایان می‌سازد.

– تقسیم (Splitting): فرآیند تقسیم یک گره به دو یا چند گره فرعی با استفاده از یک معیار تقسیم و یک ویژگی انتخاب‌شده.

– شاخه/زیردرخت (Branch/Sub-Tree): یک بخش از درخت تصمیم که از یک گره داخلی شروع شده و در گره‌های برگ پایان می‌یابد.

– گره والدین (Parent Node): گره‌ای که به یک یا چند گره فرزند تقسیم می‌شود.

– گره فرزند (Child Node): گره‌هایی که در هنگام تقسیم یک گره والدین پدید می‌آیند.

– ناخالصی (Impurity): اندازه‌گیری یکنواختی متغیر هدف در زیرمجموعه‌ای از داده. به میزان تصادف یا عدم اطمینان در یک مجموعه نمونه اشاره دارد. شاخص Gini و آنتروپی دو اندازه‌گیری متداول ناخالصی (عدم قطعیت) در درخت تصمیم برای وظایف دسته‌بندی هستند.

– تنوع (Variance): تنوع میزان تغییرات متغیرهای پیش‌بینی شده و متغیر هدف در نمونه‌های مختلف مجموعه داده را اندازه‌گیری می‌کند. این عمل برای وظایف رگرسیون در درخت تصمیم استفاده می‌شود.

– بهره اطلاعاتی (Information Gain): بهره اطلاعاتی اندازه‌گیری کاهش ناخالصی حاصل از تقسیم یک مجموعه داده بر اساس یک ویژگی خاص در درخت تصمیم است. معیار تقسیم توسط ویژگی انتخاب می‌شود که بیشترین بهره اطلاعاتی را ارائه می‌دهد و برای تعیین ویژگی با بیشترین اطلاعات در هر گره از درخت استفاده می‌شود.

– تقویت (Pruning): فرآیند حذف شاخه‌ها از درخت که هیچ اطلاعات اضافی ارائه نمی‌دهند یا به بیش‌برازش منجر می‌شوند.

اندازه‌گیری انتخاب ویژگی (Attribute Selection Measures)

ساختار درخت تصمیم

برای ساخت یک درخت تصمیم، مجموعه اصلی داده را بر اساس اندازه‌گیری انتخاب ویژگی به زیرمجموعه‌هایی تقسیم می‌کنیم. اندازه‌گیری انتخاب ویژگی (ASM) یک معیار است که در الگوریتم‌های درخت تصمیم به کار می‌رود تا اهمیت ویژگی‌های مختلف را برای تقسیم مجموعه داده ارزیابی کند.

هدف از ASM شناسایی ویژگی است که پس از تقسیم، زیرمجموعه‌های داده با بیشترین یکنواختی را ایجاد کند و اطلاعات را بیشینه کند. این فرآیند به صورت بازگشتی در هر زیرمجموعه که از تقسیم بدست می‌آید تکرار می‌شود، این فرآیند به نام “تقسیم بازگشتی” شناخته می‌شود.

بازگشت تا زمانی ادامه می‌یابد که زیرمجموعه در یک گره همه مقادیر متغیر هدف یکسان باشند یا زمانی که تقسیم دیگر به پیش‌بینی ارزش افزوده نداشته باشد. ساخت یک دسته‌بند درخت تصمیم نیازی به دانش حوزه خاص یا تنظیم پارامتر ندارد و به همین دلیل برای کشف دانش‌های کاوشی مناسب است. درخت‌های تصمیم قابلیت کار با داده‌های با ابعاد بالا را دارا هستند.

آنتروپی

آنتروپی اندازه‌گیری درجه تصادف یا عدم قطعیت در مجموعه داده است. در موارد دسته‌بندی، این معیار بر اساس توزیع برچسب‌های کلاس در مجموعه داده، میزان تصادف را اندازه‌گیری می‌کند.

پیاده سازی رگرسیون خطی در پایتون

آنتروپی برای زیرمجموعه‌ای از مجموعه داده اصلی با K تعداد کلاس برای گره i ام می‌تواند به صورت زیر تعریف شود:

که:

– S نمونه مجموعه داده است.

– k کلاس خاصی از K کلاسهاست.

– p(k) نسبت نقاط داده که به کلاس k تعلق دارند به تعداد کل نقاط در نمونه مجموعه داده S است.

(که در آن I(y=k) نشان‌دهنده تابع نشانگر است که اگر y برابر با k باشد، مقدار 1 و در غیر این صورت مقدار 0 خواهد بود.)

در اینجا باید توجه داشت کهp(i,k) نباید برابر با صفر باشد.

نکات مهم مربوط به آنتروپی

آنتروپی هنگامی که مجموعه داده کاملاً یکنواخت باشد، به این معنا که هر نمونه به یک کلاس تعلق دارد، برابر با صفر است. این کمترین آنتروپی است که نشان‌دهنده عدم تردید در نمونه مجموعه داده است.
زمانی که مجموعه داده به چند کلاس به صورت مساوی تقسیم شود، آنتروپی به حداکثر خود می‌رسد. بنابراین، آنتروپی در حالت توزیع یکنواخت بالاترین مقدار خود را دارد که نشان‌دهنده حداکثر عدم قطعیت در نمونه مجموعه داده است.
آنتروپی برای ارزیابی کیفیت یک تقسیم استفاده می‌شود. هدف آنتروپی انتخاب ویژگی است که آنتروپی زیرمجموعه‌های نتیجه را با تقسیم مجموعه داده به زیرمجموعه‌هایی با یکنواختی بیشتر نسبت به برچسب‌های کلاس به حداقل برساند.
ویژگی با بالاترین بهره اطلاعاتی (کاهش آنتروپی پس از تقسیم بر اساس آن ویژگی) به عنوان معیار تقسیم انتخاب می‌شود، و فرآیند به صورت بازگشتی تکرار می‌شود تا درخت تصمیم ساخته شود.

ناخالصی یا شاخص Gini

ناخالصی یا شاخص Gini یک امتیاز است که ارزیابی می‌کند چقدر یک تقسیم در بین گروه‌های دسته‌بندی شده دقیق است. ناخالصی Gini یک امتیاز را در بازه بین 0 تا 1 ارزیابی می‌کند، که 0 هنگامی است که همه مشاهدات به یک کلاس تعلق دارند و 1 توزیع تصادفی عناصر در داخل کلاس‌ها است. در این حالت، ما می‌خواهیم که نمره ناخالصی Gini حداقل باشد. شاخص Gini معیار ارزیابی است که برای ارزیابی مدل درخت تصمیم استفاده می‌شود.

که:

– p_i نسبت عناصر موجود در مجموعه که به دسته i ام تعلق دارند، است.

بهره اطلاعاتی

بهره اطلاعاتی اندازه‌گیری کاهش در آنتروپی یا واریانس است که ناشی از تقسیم یک مجموعه داده بر اساس یک خصوصیت خاص است. این اندازه‌گیری در الگوریتم‌های درخت تصمیم برای تعیین اهمیت یک ویژگی با تقسیم مجموعه داده به زیرمجموعه‌هایی با یکنواختی بیشتر نسبت به برچسب‌های کلاس یا متغیر هدف استفاده می‌شود. هر چه بهره اطلاعاتی بیشتر باشد، ویژگی ارزشمندتری در پیش‌بینی متغیر هدف است.

بهره اطلاعاتی ویژگی A نسبت به مجموعه داده S به صورت زیر محاسبه می‌شود:

که:

– A ویژگی یا برچسب کلاس خاصی است.

– |H| آنتروپی نمونه مجموعه داده S است.

– |HV| تعداد نمونه‌ها در زیرمجموعه S است که مقدار v برای ویژگی A دارند.

بهره اطلاعاتی میزان کاهش آنتروپی یا واریانس را که با تقسیم مجموعه داده بر اساس ویژگی A حاصل می‌شود اندازه‌گیری می‌کند. ویژگی که بهره اطلاعاتی را بیشینه می‌کند، به عنوان معیار تقسیم برای ساخت درخت تصمیم انتخاب می‌شود.

بهره اطلاعاتی در هر دو درخت تصمیم دسته‌بندی و درخت تصمیم رگرسیون استفاده می‌شود. در دسته‌بندی، آنتروپی به عنوان اندازه‌گیری برای ناخالصی استفاده می‌شود، در حالی که در رگرسیون واریانس به عنوان اندازه‌گیری برای ناخالصی مورد استفاده قرار می‌گیرد. محاسبه بهره اطلاعاتی در هر دو حالت یکسان است، تنها تفاوت این است که در فرمول به جای آنتروپی یا اندازه‌گیری ناخالصی، آنتروپی یا واریانس به کار می‌رود.

الگوریتم درخت تصمیم چطور عمل می کند؟

الگوریتم درخت تصمیم با تجزیه و تحلیل مجموعه داده به منظور پیش‌بینی دسته‌بندی آن عمل می‌کند. این عمل از گره ریشه درخت شروع می‌شود، جایی که الگوریتم مقدار ویژگی گره را با ویژگی رکورد در مجموعه داده واقعی مقایسه می‌کند. بر اساس این مقایسه، الگوریتم به سمت شاخه می‌رود و به گره بعدی منتقل می‌شود.

الگوریتم این عمل را برای گره‌های بعدی تکرار می‌کند، با مقایسه مقادیر ویژگی‌های آن با مقادیر زیر-گره‌ها و ادامه این فرآیند. این تکرار تا زمانی ادامه پیدا می‌کند که به گره برگ درخت برسد. مکانیزم کامل می‌تواند از طریق مراحل زیر بهتر توضیح داده شود.

مرحله ۱: شروع درخت با گره ریشه به نام S که داده کلی را شامل می‌شود.
مرحله ۲: با استفاده از اندازه‌گیری انتخاب ویژگی (ASM)، بهترین ویژگی را در مجموعه داده پیدا کنید.
مرحله ۳: مجموعه S را به زیرمجموعه‌هایی تقسیم کنید که شامل مقادیر ممکن برای بهترین ویژگی هستند.
مرحله ۴: گره درخت تصمیم را ایجاد کنید که بهترین ویژگی را شامل می‌شود.
مرحله ۵: به صورت بازگشتی درخت‌های تصمیم جدید را با استفاده از زیرمجموعه‌های مجموعه داده ساخته شده در مرحله ۳ بسازید. این فرآیند را تا زمانی ادامه دهید که به یک مرحله برسید که نمی‌توانید گره‌ها را به صورت بیشتر دسته‌بندی کنید که این گره به عنوان یک گره برگ نهایی نامیده می‌شود.

رگرسیون خطی با کتابخانه sklearn

مزایای درخت تصمیم

ساده در درک: این الگوریتم به دلیل دنبال کردن همان فرآیندی که انسان‌ها در تصمیم‌گیری واقعی دنبال می‌کنند، بسیار ساده و قابل درک است.
کاربردی برای حل مسائل تصمیم‌گیری: بسیار مفید برای حل مسائل مرتبط با تصمیم‌گیری است.
کمک به تفکر درباره تمام نتایج ممکن یک مسئله: به تفکر درباره تمام نتایج ممکن برای یک مسئله کمک می‌کند.
نیاز کمتر به تمیزکاری داده نسبت به سایر الگوریتم‌ها: نسبت به الگوریتم‌های دیگر، نیاز کمتری به پاکسازی داده دارد.

معایب درخت تصمیم

پیچیدگی: درخت تصمیم شامل تعداد زیادی لایه است که آن را پیچیده می‌کند.
ممکن است با مشکل بیش‌برازش (Overfitting) روبرو شود، که با استفاده از الگوریتم جنگل تصادفی قابل حل است.
برای تعداد بیشتری از برچسب‌های کلاس، پیچیدگی محاسباتی درخت تصمیم ممکن است افزایش یابد.

مسائل مناسب برای یادگیری درخت تصمیم

اگرچه روش‌های مختلفی برای یادگیری درخت تصمیم با قابلیت‌ها و نیازهای کمی توسعه یافته‌اند، اما به طور کلی یادگیری درخت تصمیم بهترین عملکرد را در مسائل با ویژگی‌های زیر ارائه می‌دهد:

نمونه‌ها توسط جفت ویژگی-ارزش نمایانده می‌شوند:

در دنیای یادگیری درخت تصمیم، معمولاً از جفت ویژگی-ارزش برای نمایش نمونه‌ها استفاده می‌شود. یک نمونه توسط یک گروه از پیش‌تعیین شده ویژگی‌ها نظیر دما و مقدار متناظر آن مانند گرم، تعریف می‌شود. بهتر است هر ویژگی مجموعه محدودی از ارزش‌های متمایز مانند گرم، معتدل یا سرد را داشته باشد. این باعث سهولت در ساخت درخت‌های تصمیم می‌شود. با این حال، نسخه‌های پیشرفته‌تر الگوریتم می‌توانند ویژگی‌ها با ارزش‌های عددی پیوسته را هم جا به جا کنند، مثل نمایش دما با یک مقیاس عددی.

تابع هدف مقادیر خروجی گسسته دارد:

هدف مشخص شده دارای نتایج متمایز است. روش درخت تصمیم معمولاً برای دسته‌بندی نمونه‌های بولین مانند بله یا خیر استفاده می‌شود. روش‌های درخت تصمیم به راحتی گسترش می‌یابند تا توانایی دستیابی به توابع با بیش از دو مقدار خروجی ممکن را داشته باشند. گسترش بزرگتر به ما این امکان را می‌دهد که درباره اهداف با خروجی‌های عددی اطلاعات کسب کنیم، هرچند که کاربرد درخت تصمیم در این چارچوب نسبت به موارد دیگر نسبتاً کمتر است.

توصیفات گسسته ممکن است لازم باشد:

درخت‌های تصمیم به طور طبیعی توصیفات گسسته را نمایندگی می‌کنند.

داده‌های آموزش ممکن است حاوی خطاها باشند:

تکنیک‌های یادگیری درخت تصمیم مقاومت بالایی در برابر اختلافات نشان می‌دهند، از جمله عدم انطباق در دسته‌بندی موارد نمونه و عدم انطباق در جزئیات ویژگی‌ها که مشخصه این موارد است.

داده‌های آموزش ممکن است حاوی مقادیر ویژگی ناقص باشد:

در برخی موارد، اطلاعات ورودی طراحی شده برای آموزش ممکن است دارای ویژگی‌های گم‌شده باشد. استفاده از روش‌های درخت تصمیم همچنان ممکن است حتی در صورت وجود ویژگی‌های ناشناخته در برخی از نمونه‌های آموزشی باشد. به عنوان مثال، در نظر گرفتن سطح رطوبت طول روز، این اطلاعات ممکن است تنها برای یک مجموعه خاص از نمونه‌های آموزشی در دسترس باشد.

مسائل عملی در یادگیری درخت تصمیم

تعیین عمق مناسب برای رشد درخت تصمیم.
مدیریت ویژگی‌های پیوسته.
انتخاب اندازه ویژگی مناسب.
مدیریت داده‌های آموزشی با مقادیر ویژگی گم‌شده.
مدیریت ویژگی‌ها با هزینه‌های متفاوت.
بهبود کارایی محاسباتی.

برای ساخت درخت تصمیم از الگوریتم CART (Classification and Regression Tree) استفاده می‌شود. این الگوریتم با انتخاب بهترین تقسیم در هر گره بر اساس معیارهایی مانند ناخالصی Gini یا Information Gain عمل می‌کند تا یک درخت تصمیم ایجاد شود. در زیر مراحل اصلی الگوریتم CART آورده شده است:

گره ریشه درخت باید مجموعه داده‌های آموزشی کامل باشد.
ناخالصی داده بر اساس هر ویژگی موجود در مجموعه داده تعیین می‌شود. ناخالصی می‌تواند با استفاده از معیارهایی مانند شاخص Gini یا آنتروپی برای دسته‌بندی و خطای میانگین مربعات، خطای میانگین مطلق، friedman_mse یا نیمی از انحراف پواسون برای رگرسیون اندازه‌گیری شود.
سپس ویژگی را انتخاب می‌کند که در تقسیم داده حاصل از آن، بیشترین بهره اطلاعات یا کاهش ناخالصی را به دنبال دارد.
برای هر مقدار ممکن ویژگی انتخاب شده، مجموعه داده را به دو زیرمجموعه (چپ و راست) تقسیم می‌کند؛ یکی که ویژگی این مقدار را دارد و دیگری که ندارد. تقسیم باید طراحی شود تا زیرمجموعه‌ها نسبت به متغیر هدف به حد امکان خالص باشند.
بر اساس متغیر هدف، ناخالصی هر زیرمجموعه حاصل را تعیین می‌کند.
برای هر زیرمجموعه، مراحل 2 تا 5 را به صورت بازگشتی تکرار می‌کند تا یکی از شرایط توقف حاصل شود؛ به عنوان مثال، می‌تواند شرایطی مانند حداکثر عمق درخت، حداقل تعداد نمونه‌های مورد نیاز برای تقسیم یا حداقل آستانه ناخالصی باشد.
برای هر گره پایانی (گره برگ) در درخت، برچسب کلاس اکثریت برای مسائل دسته‌بندی یا مقدار میانگین برای مسائل رگرسیون اختصاص داده می‌شود.

کاربرد بیز ساده چند جمله‌ای در مسائل پردازش زبان طبیعی (NLP)

الگوریتم درخت تصمیم برای دسته‌بندی

فرض کنید داده‌های موجود در گره m با Q_m نمایش داده شده و تعداد n_m نمونه دارد و t_m حد نمونه m است. سپس، الگوریتم درخت تصمیم برای دسته‌بندی می‌تواند به صورت زیر نوشته شود:

در اینجا:

– H اندازه‌گیری ناخالصی‌‌های زیرمجموعه‌های چپ و راست در گره m است. این می‌تواند آنتروپی یا ناخالصی Gini باشد.

– n_m تعداد نمونه‌ها در زیرمجموعه‌های چپ و راست در گره m است.

برای انتخاب پارامتر، می‌توانیم به صورت زیر بنویسیم:

# Import the necessary libraries
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn.tree import export_graphviz
from graphviz import Source

# Load the dataset
iris = load_iris()
X = iris.data[:, 2:] # petal length and width
y = iris.target

# DecisionTreeClassifier
tree_clf = DecisionTreeClassifier(criterion='entropy',
								max_depth=2)
tree_clf.fit(X, y)

# Plot the decision tree graph
export_graphviz(
	tree_clf,
	out_file="iris_tree.dot",
	feature_names=iris.feature_names[2:],
	class_names=iris.target_names,
	rounded=True,
	filled=True
)

with open("iris_tree.dot") as f:
	dot_graph = f.read()
	
Source(dot_graph)

الگوریتم درخت تصمیم برای رگرسیون

فرض کنید داده‌های موجود در گره m با Q_m نمایش داده شده و تعداد n_m نمونه دارد و t_m حد نمونه m است. سپس، الگوریتم درخت تصمیم برای رگرسیون می‌تواند به صورت زیر نوشته شود:

در اینجا:

– MSE میانگین خطای مربعات است.

که در آن:

– n_m تعداد نمونه‌ها در زیرمجموعه‌های چپ و راست در گره m است.

برای انتخاب پارامتر، می‌توانیم به صورت زیر بنویسیم:

# Import the necessary libraries
from sklearn.datasets import load_diabetes
from sklearn.tree import DecisionTreeRegressor
from sklearn.tree import export_graphviz
from graphviz import Source

# Load the dataset
diabetes = load_diabetes()
X = diabetes.data
y = diabetes.target

# DecisionTreeRegressor
tree_reg = DecisionTreeRegressor(criterion = 'squared_error',
								max_depth=2)

tree_reg.fit(X, y)

# Plot the decision tree graph
export_graphviz(
	tree_reg,
	out_file="diabetes_tree.dot",
	feature_names=diabetes.feature_names,
	class_names=diabetes.target,
	rounded=True,
	filled=True
)

with open("diabetes_tree.dot") as f:
	dot_graph = f.read()
	
Source(dot_graph)

نقاط قوت روش درخت تصمیم

– درخت‌های تصمیم قوانین قابل فهمی ایجاد می‌کنند.

– درخت‌های تصمیم دسته‌بندی را بدون نیاز به محاسبات زیادی انجام می‌دهند.

– درخت‌های تصمیم می‌توانند با متغیرهای پیوسته و دسته‌ای هر دو کار کنند.

– درخت‌های تصمیم نشان می‌دهند که کدام فیلدها برای پیش‌بینی یا دسته‌بندی حیاتی‌تر هستند.

– سادگی استفاده: درخت‌های تصمیم استفاده آسانی دارند و نیاز به تخصص فنی زیادی ندارند، که آنها را برای یک دسته وسیع از کاربران قابل دسترس می‌سازد.

– قابلیت مقیاس‌پذیری: درخت‌های تصمیم می‌توانند با مجموعه‌داده‌های بزرگ کار کنند و به راحتی می‌توانند به صورت موازی شوند تا زمان پردازش را بهبود بخشند.

– تحمل مقدار گم‌شده: درخت‌های تصمیم می‌توانند با مقادیر گم‌شده در داده کار کنند که این امر آنها را به گزینه مناسبی برای کار با مجموعه‌داده‌هایی با داده‌های گم‌شده یا ناقص می‌کند.

– مدیریت روابط غیرخطی: درخت‌های تصمیم می‌توانند با روابط غیرخطی بین متغیرها کار کنند که این امر آنها را به گزینه مناسبی برای کار با مجموعه‌داده‌های پیچیده می‌کند.

– توانایی مدیریت داده‌های نامتوازن: درخت‌های تصمیم می‌توانند با مجموعه‌داده‌های نامتوازن، جایی که یک کلاس نسبت به دیگران شدیداً نماینده است، با توزیع اهمیت گره‌های فردی بر اساس توزیع کلاس، کار کنند.

نقاط ضعف‌ روش درخت تصمیم

درخت‌های تصمیم کمتر مناسب برای وظایف تخمینی هستند که هدف پیش‌بینی مقدار یک ویژگی پیوسته باشد.
در مسائل دسته‌بندی با تعداد زیادی کلاس و تعداد محدودی نمونه آموزشی، درخت‌های تصمیم ممکن است به اشتباه برخی از کلاس‌ها را تشخیص دهند.
آموزش درخت‌های تصمیم ممکن است محاسباتی سنگین باشد. فرآیند رشد یک درخت تصمیم محاسباتی سنگین است. در هر گره، هر فیلد تقسیم‌بندی ممکن باید قبل از یافتن بهترین تقسیم مرتب شود. در برخی از الگوریتم‌ها، ترکیب‌هایی از فیلدها استفاده می‌شود و باید برای وزن‌دهی بهینه به ترکیبات جستجو شود. الگوریتم‌های کاشت نیز ممکن است ثقیل باشند زیرا باید زیردرخت‌های فرعی ممکن تشکیل و مقایسه شوند.
درخت‌های تصمیم به بیش‌برازش داده‌های آموزش حساس هستند، به‌ویژه زمانی که درخت بسیار عمیق یا پیچیده است. این ممکن است منجر به عملکرد نادرست بر روی داده‌های جدید و ناشناخته شود.
تغییرات کوچک در داده‌های آموزش می‌تواند منجر به تولید درخت‌های تصمیم مختلف شود، که ممکن است مشکلی در مقایسه یا بازتولید نتایج باشد.
بسیاری از الگوریتم‌های درخت تصمیم با داده‌های گم‌شده خوب کار نمی‌کنند و نیاز به تخمین یا حذف رکوردهای دارای مقادیر گم‌شده دارند.
معیارهای تقسیم اولیه استفاده‌شده در الگوریتم‌های درخت تصمیم ممکن است منجر به تولید درخت‌های تکراری شود، به‌ویژه زمانی که با مجموعه‌داده‌های نامتوازن یا کلاس‌های کمی سر و کار داریم.
درخت‌های تصمیم در توانایی نمایش روابط پیچیده بین متغیرها محدود هستند، به‌ویژه زمانی که با اثرات غیرخطی یا تعاملی مواجه هستیم.
درخت‌های تصمیم ممکن است به مقیاس‌گذاری ویژگی‌های ورودی حساس باشند، به‌ویژه زمانی که از معیارها یا قوانین تصمیمی که بر مقایسه بین مقادیر تکیه می‌کنند، استفاده می‌شود.

پیاده‌سازی با پایتون 3

from sklearn.datasets import make_classification
from sklearn import tree
from sklearn.model_selection import train_test_split

X, t = make_classification(100, 5, n_classes=2, shuffle=True, random_state=10)
X_train, X_test, t_train, t_test = train_test_split(
	X, t, test_size=0.3, shuffle=True, random_state=1)

model = tree.DecisionTreeClassifier()
model = model.fit(X_train, t_train)

predicted_value = model.predict(X_test)
print(predicted_value)

tree.plot_tree(model)

zeroes = 0
ones = 0
for i in range(0, len(t_train)):
	if t_train[i] == 0:
		zeroes += 1
	else:
		ones += 1

print(zeroes)
print(ones)

val = 1 - ((zeroes/70)*(zeroes/70) + (ones/70)*(ones/70))
print("Gini :", val)

match = 0
UnMatch = 0

for i in range(30):
	if predicted_value[i] == t_test[i]:
		match += 1
	else:
		UnMatch += 1

accuracy = match/30
print("Accuracy is: ", accuracy)

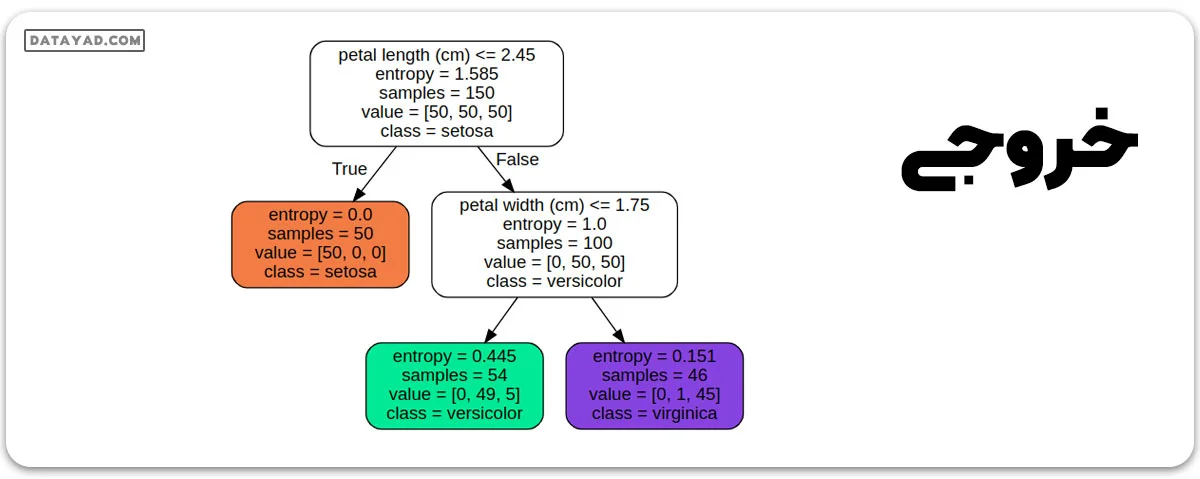
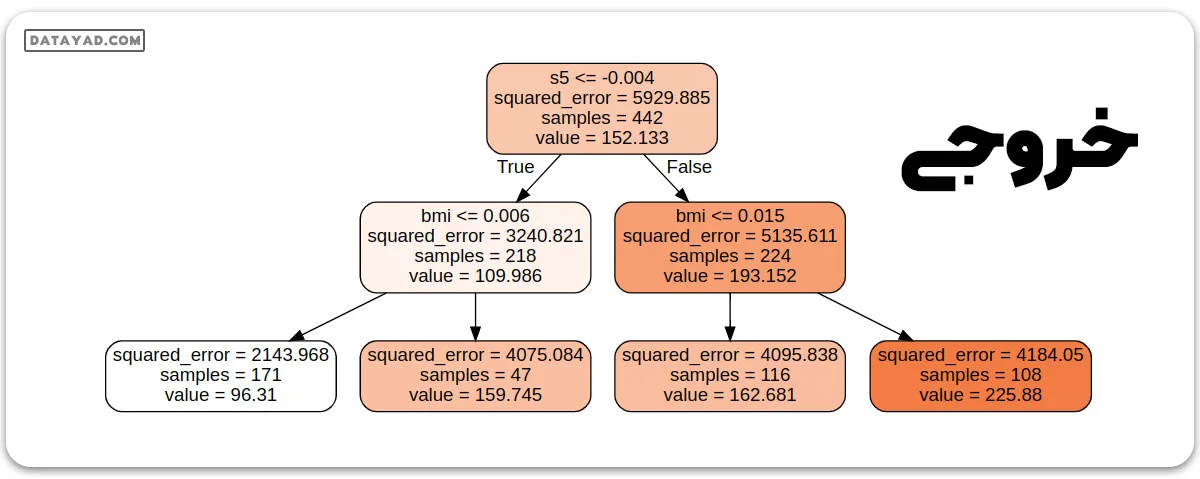
خروجی:

1 1 0 0 1 0 1 0 1 0 0 1 1 0 0 1 0 1 1 1 0 0 0 1 1 0 0 0 1 0 
Gini : 0.5
Accuracy is: 0.366667

Rating 5.00 from 1 votes

لیست دروس دوره

آموزش پیشنهادی و مکمل

اگر سوالی در مورد این درس دارید، در کادر زیر بنویسید.

0 نظرات

بازخورد (Feedback) های اینلاین

مشاهده همه دیدگاه ها