رگرسیون چندجمله ای یک نوع از رگرسیون خطی است که در آن رابطه بین متغیر مستقل x و متغیر وابسته y به صورت یک چندجملهای درجه n مدلسازی میشود. رگرسیون چندجملهای یک رابطه غیرخطی بین مقدار x و میانگین شرطی متناظر y، که با E(y | x) نشان داده میشود، برازش میکند. در این درس می خواهیم به پیاده سازی رگرسیون چندجمله ای با پایتون بپردازیم.
رگرسیون چندجملهای چیست؟
گاهی اوقات، محققان با روابطی روبرو میشوند که به نظر منحنی میرسند. در چنین حالاتی، استفاده از عبارات چندجملهای ضروری است.
بررسی باقیماندهها نشان میدهد که اگر بخواهیم دادههای منحنیشکل را با یک مدل خطی برازش کنیم، نمودار پراکندگی باقیماندهها (روی محور Y) نسبت به پیشبینها (روی محور X)، دارای مناطقی با باقیماندههای مثبت زیاد خواهد بود. بنابراین، استفاده از مدلهای خطی در این شرایط مناسب نیست.
در تحلیل رگرسیون خطی چندگانه معمول، فرض میشود که همه متغیرهای مستقل، از هم مستقل هستند. اما در مدل رگرسیون چندجملهای، این فرض برقرار نیست.
چگونگی کارکرد رگرسیون چندجملهای
اگر با دقت بیشتری نگاه کنیم، میفهمیم که برای گذار از رگرسیون خطی به رگرسیون چندجملهای، فقط لازم است که جملات درجه بالای ویژگیهای وابسته را به مجموعه ویژگیها اضافه کنیم. این فرایند گاهی اوقات به عنوان مهندسی ویژگی شناخته میشود، اما دقیقاً همان نیست.
کاربردهای رگرسیون چندجملهای
دلیل استفاده گسترده از رگرسیون چندجملهای این است که تقریباً تمام دادههای دنیای واقعی به طور طبیعی غیرخطی هستند و به همین دلیل، وقتی مدل غیرخطی را روی دادهها اعمال میکنیم یا خط رگرسیون منحنیشکلی را برازش میکنیم، نتایجی که به دست میآوریم، به مراتب بهتر از آنچه با رگرسیون خطی معمولی به دست میآید، میباشد. برخی از کاربردهای رگرسیون چندجملهای عبارتند از:
- نرخ رشد بافتها
- پیشرفت اپیدمی بیماریها
- توزیع ایزوتوپهای کربن در رسوبات دریاچهها
هدف اصلی تحلیل رگرسیون مدلسازی مقدار مورد انتظار یک متغیر وابسته y بر اساس مقدار یک متغیر مستقل x است. در رگرسیون خطی ساده، از معادله زیر استفاده میکنیم:
y = a + bx + e
در اینجا y یک متغیر وابسته است،
a نقطه تقاطع با محور y،
b شیب خط و e نرخ خطا میباشد.
در بسیاری از موارد، این مدل خطی کاربرد نخواهد داشت. برای مثال، اگر تولید سنتز شیمیایی را بر اساس دمایی که سنتز در آن انجام میشود تحلیل کنیم، در چنین مواردی از یک مدل درجه دوم استفاده میکنیم:
y = a + b1x + b2x^2 + e
در اینجا y متغیر وابسته به x است، a نقطه تقاطع با محور y و e نرخ خطا است. به طور کلی، میتوانیم آن را برای مقدار nام مدلسازی کنیم.
y = a + b1x + b2x^2 + … + bnx^n
چون تابع رگرسیون در مورد متغیرهای نامعلوم به صورت خطی است، این مدلها از دیدگاه برآورد، خطی به شمار میروند. بنابراین، با استفاده از روش کمترین مربعات، مقدار واکنش، یعنی y را محاسبه کنیم.
پیاده سازی رگرسیون چندجمله ای با پایتون
برای دسترسی به مجموعه دادهای که برای تحلیل رگرسیون چندجملهای استفاده شده است، اینجا کلیک کنید. کتابخانههای مهم و مجموعه دادهای که برای انجام رگرسیون چندجملهای استفاده میکنیم را وارد کنید.
کتابخانههای پایتون به ما کمک میکنند تا به راحتی دادهها را مدیریت کنیم و کارهای معمول و پیچیده را تنها با یک خط کد انجام دهیم، می توانیم از کتابخانه های پایتون زیر برای پیاده سازی رگرسیون چندجمله ای استفاده کنیم:
✔️Pandas: این کتابخانه به ما کمک میکند تا دادهها را در قالب آرایه ۲ بعدی بارگذاری کنیم و دارای توابع متعددی برای انجام وظایف تحلیلی به صورت یکجا است.
✔️Numpy: آرایههای نامپای بسیار سریع هستند و میتوانند محاسبات بزرگ را در زمان بسیار کوتاهی انجام دهند.
✔️Matplotlib/Seaborn: این کتابخانه برای ترسیم نمودارهای تجسمی استفاده میشود.
✔️Sklearn: این ماژول شامل چندین کتابخانه با توابع پیادهسازی شده پیشین است که وظایفی از پیشپردازش داده تا توسعه و ارزیابی مدل را انجام میدهند.
# Importing the libraries
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# Importing the dataset
datas = pd.read_csv('data.csv')
datas
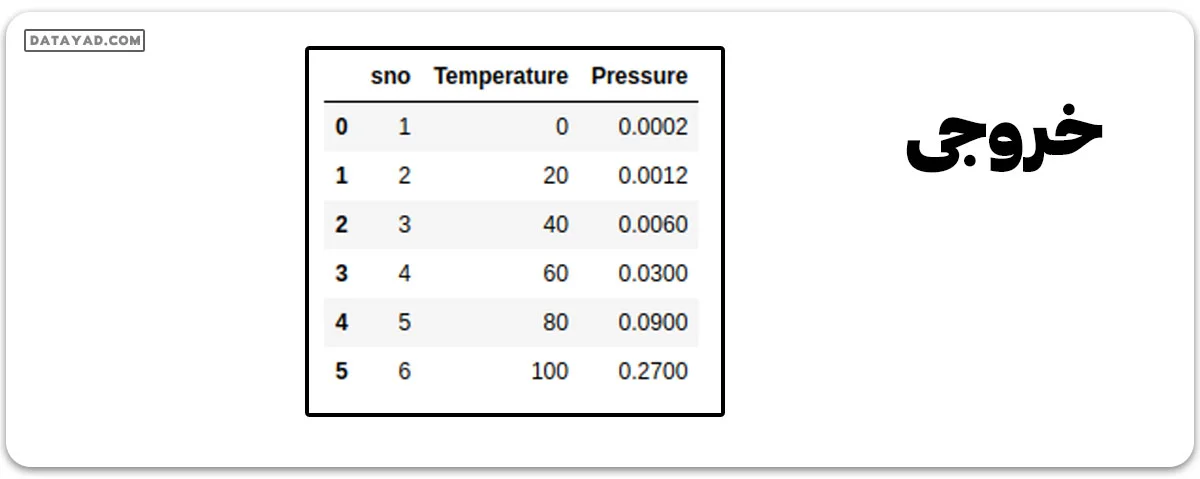
متغیر ویژگی ما که X است، شامل ستونهای بین اولین تا قبل از متغیر هدف خواهد بود که y نام دارد و متغیر هدف، یعنی y، شامل ستون دوم خواهد بود.
X = datas.iloc[:, 1:2].values y = datas.iloc[:, 2].values
حالا بیایید یک مدل رگرسیون خطی را روی دادههای موجود برازش کنیم.
# Features and the target variables X = datas.iloc[:, 1:2].values y = datas.iloc[:, 2].values # Fitting Linear Regression to the dataset from sklearn.linear_model import LinearRegression lin = LinearRegression() lin.fit(X, y)
برازش مدل رگرسیون چندجملهای روی دو جزء X و y.
# Fitting Polynomial Regression to the dataset from sklearn.preprocessing import PolynomialFeatures poly = PolynomialFeatures(degree=4) X_poly = poly.fit_transform(X) poly.fit(X_poly, y) lin2 = LinearRegression() lin2.fit(X_poly, y)
در این مرحله، ما نتایج رگرسیون خطی را با استفاده از یک نمودار پراکندگی بصریسازی میکنیم.
# Visualising the Linear Regression results
plt.scatter(X, y, color='blue')
plt.plot(X, lin.predict(X), color='red')
plt.title('Linear Regression')
plt.xlabel('Temperature')
plt.ylabel('Pressure')
plt.show()
بصریسازی نتایج رگرسیون چندجملهای با استفاده از نمودار پراکندگی.
# Visualising the Polynomial Regression results
plt.scatter(X, y, color='blue')
plt.plot(X, lin2.predict(poly.fit_transform(X)),
color='red')
plt.title('Polynomial Regression')
plt.xlabel('Temperature')
plt.ylabel('Pressure')
plt.show()
پیشبینی نتایج جدید با استفاده از هر دو رگرسیون خطی و چندجملهای. توجه داشته باشید که متغیر ورودی باید در یک آرایه ۲ بعدی Numpy باشد.
# Predicting a new result with Linear Regression # after converting predict variable to 2D array pred = 110.0 predarray = np.array([[pred]]) lin.predict(predarray)
خروجی:
array([0.20675333])
# Predicting a new result with Polynomial Regression # after converting predict variable to 2D array pred2 = 110.0 pred2array = np.array([[pred2]]) lin2.predict(poly.fit_transform(pred2array))
خروجی:
array([0.43295877])
بیشبرازش در مقابل کمبرازش
در هنگام کار با رگرسیون چندجملهای، یکی از مشکلاتی که اغلب با آن روبرو میشویم، مسئله بیشبرازش است. این مشکل زمانی رخ میدهد که ما برای بهبود عملکرد مدل، درجه رگرسیون چندجملهای را افزایش میدهیم، اما این کار باعث میشود مدل بیش از حد روی دادههای موجود تنظیم شود و عملکرد آن روی دادههای جدید نامطلوب باشد.
به همین خاطر، وقتی از رگرسیون چندجملهای استفاده میکنیم، معمولاً سعی میکنیم وزنهای مدل را به منظور مقابله با مشکل بیشبرازش تنظیم کنیم. برای این منظور، از تکنیکهای تنظیم مانند رگرسیون لاسو و ریج استفاده میشود، به خصوص در شرایطی که احتمال دارد مدل روی دادهها بیش از حد تنظیم شود.
تعادل میان بایاس و واریانس
این روش، گستردهترین شکل رویکردی است که برای دوری از مشکلات بیشبرازش و کمبرازش استفاده میشود. در این روش هم، ما از مشکل بیشبرازش دوری میکنیم با اینکه درجه مناسب چندجملهای را که میخواهیم روی دادههایمان برازش کنیم، انتخاب میکنیم. به عنوان مثال، این هدف وقتی محقق میشود که پس از افزایش درجه چندجملهای تا یک سطح معین، فاصله بین معیارهای آموزشی و اعتبارسنجی شروع به بزرگتر شدن کند.
مزایای استفاده از رگرسیون چندجمله ای
- این قابلیت را دارد که توابع گستردهای را برازش کند.
- در واقع، رگرسیون چندجمله ای به خوبی به منحنیهای مختلف را انطباق میدهد.
- بهترین تقریب رابطهای بین متغیر وابسته و مستقل را فراهم میکند.
معایب استفاده از رگرسیون چندجمله ای
- حساسیت بیش از حد نسبت به دادههای نویزی: حضور یک یا دو داده نویزی در دادهها میتواند به شدت بر نتایج تحلیل غیرخطی تأثیر بگذارد.
- علاوه بر این، ابزارهای کمتری برای تشخیص دادههای نویزی در رگرسیون غیرخطی نسبت به رگرسیون خطی موجود است.















