استفاده از SVM برای دسته‌بندی در یک مجموعه داده غیرخطی

تعریف هایپرپلین و دسته‌بند SVM

در صورتی که مجموعه داده به صورت خطی جداپذیر باشد و دارای n ویژگی باشد (بنابراین برای نمایش نیاز به n بُعد دارد)، هایپرپلین اساساً یک زیرفضای (n-1) بُعدی است که برای جدا کردن مجموعه داده به دو دسته مورد استفاده قرار می‌گیرد. هر دسته شامل نقاط داده‌ای از یک کلاس متفاوت می‌شود.

به عنوان مثال، برای یک مجموعه داده با دو ویژگی X و Y (بنابراین در فضای دو بُعدی واقع شده است)، هایپرپلین جداکننده یک خط (که یک زیرفضای یک بُعدی است) است. به همین ترتیب، برای یک مجموعه داده با سه بُعد، هایپرپلین جداکننده دارای زیرفضای دو بُعدی است و به همین ترتیب ادامه پیدا می‌کند.

در یادگیری ماشین، ماشین بردار پشتیبان (SVM) یک دسته‌بند خطی و دودویی بدون احتمال است که برای دسته‌بندی داده‌ها از طریق یادگیری یک هایپرپلین برای جدا کردن داده‌ها به کار می‌رود.

استفاده از ماشین بردار پشتیبان (SVM) برای دسته‌بندی مجموعه‌ای از داده‌های غیرخطی که از یک دسته‌بند خطی استفاده می‌کند: 

همانطور که گفته شد، SVM یک دسته‌بند خطی است که یک دسته‌بند با بُعد (n-1) برای دسته‌بندی داده‌ها به دو کلاس آموزش می‌بیند. با این حال، این می‌تواند برای دسته‌بندی مجموعه داده‌های غیرخطی نیز مورد استفاده قرار گیرد. این کار با ترسیم مجموعه داده به یک بُعد بالاتر انجام می‌شود که در آن داده‌ها به صورت خطی جداپذیر هستند!

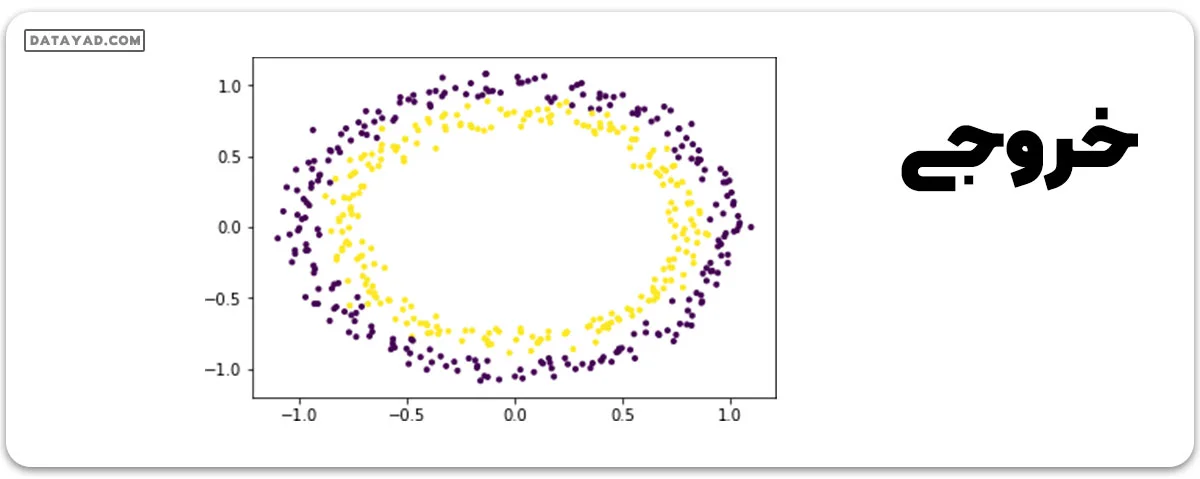
برای درک بهتر، به عنوان مثال، مجموعه داده حلقه‌ها را درنظر بگیرید.

# importing libraries 
import numpy as np 
import matplotlib.pyplot as plt 
from sklearn.datasets import make_circles 
from mpl_toolkits.mplot3d import Axes3D 

# generating data 
X, Y = make_circles(n_samples = 500, noise = 0.02) 

# visualizing data 
plt.scatter(X[:, 0], X[:, 1], c = Y, marker = '.') 
plt.show() 

مجموعه داده به وضوح یک مجموعه داده غیرخطی است و از دو ویژگی (مثلاً X و Y) تشکیل شده است.

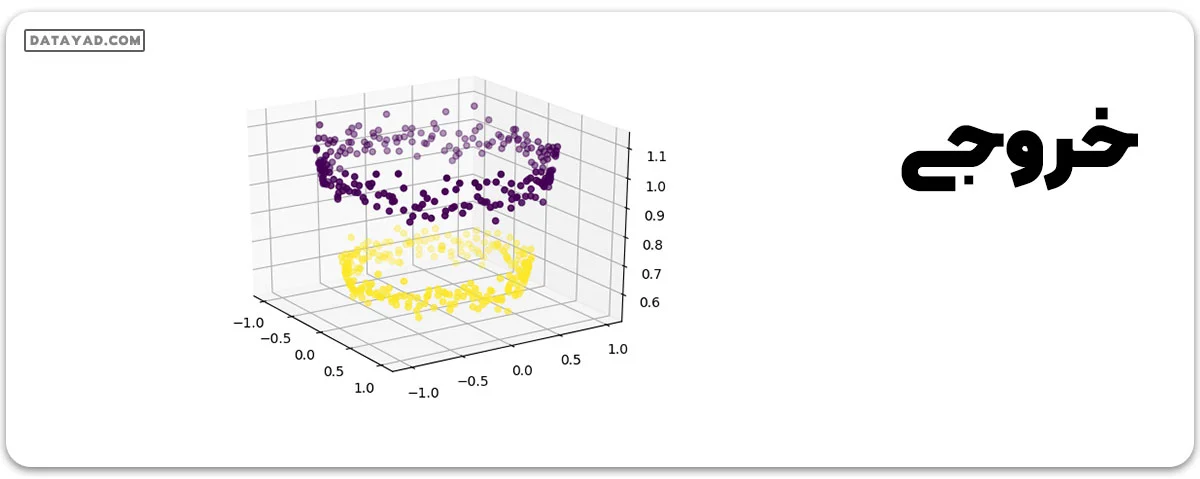
برای استفاده از SVM برای دسته‌بندی این داده، یک ویژگی دیگر به نام Z = X² + Y² را به مجموعه داده اضافه کنید. با این کار، داده دوبعدی را به فضای سه بعدی انتقال می‌دهیم. ابعاد اولیه به ترتیب ویژگی X، دومی ویژگی Y و سومی ویژگی Z را نمایان می‌کنند (که به صورت ریاضی با شعاع دایره که نقطه (x، y) به آن تعلق دارد، برابر است). حالا، به وضوح مشخص است که برای داده‌های نشان داده شده، نقاط داده زرد به یک دایره با شعاع کوچک تعلق دارند و نقاط داده بنفش به یک دایره با شعاع بزرگتر تعلق دارند. بنابراین، داده به صورت خطی جداپذیر در امتداد محور Z می‌شود.

# adding a new dimension to X 
X1 = X[:, 0].reshape((-1, 1)) 
X2 = X[:, 1].reshape((-1, 1)) 
X3 = (X1**2 + X2**2) 
X = np.hstack((X, X3)) 

# visualizing data in higher dimension 
fig = plt.figure() 
axes = fig.add_subplot(111, projection = '3d') 
axes.scatter(X1, X2, X1**2 + X2**2, c = Y, depthshade = True) 
plt.show() 

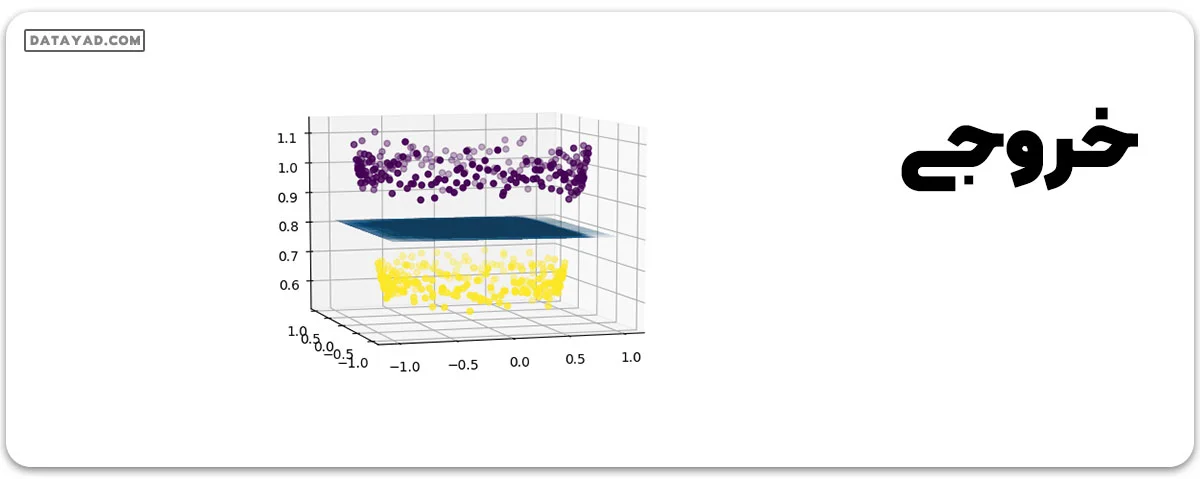
حالا می‌توانیم از SVM (یا هر دسته‌بند خطی دیگر) برای یادگیری یک هایپرپلین به صورت دو بعدی استفاده کنیم. بدین صورت هایپرپلین به شکل زیر در می‌آید:

# create support vector classifier using a linear kernel 
from sklearn import svm 

svc = svm.SVC(kernel = 'linear') 
svc.fit(X, Y) 
w = svc.coef_ 
b = svc.intercept_ 

# plotting the separating hyperplane 
x1 = X[:, 0].reshape((-1, 1)) 
x2 = X[:, 1].reshape((-1, 1)) 
x1, x2 = np.meshgrid(x1, x2) 
x3 = -(w[0][0]*x1 + w[0][1]*x2 + b) / w[0][2] 

fig = plt.figure() 
axes2 = fig.add_subplot(111, projection = '3d') 
axes2.scatter(X1, X2, X1**2 + X2**2, c = Y, depthshade = True) 
axes1 = fig.gca(projection = '3d') 
axes1.plot_surface(x1, x2, x3, alpha = 0.01) 
plt.show() 

بدین ترتیب، با استفاده از یک دسته‌بند خطی، می‌توان یک مجموعه داده غیرخطی را از یکدیگر جدا کرد.

مقدمه‌ای مختصر درباره کرنل‌ها در یادگیری ماشین

در یادگیری ماشین، از یک ترفند معروف به “ترفند کرنل” برای یادگیری یک دسته‌بند خطی به منظور دسته‌بندی مجموعه داده‌های غیرخطی استفاده می‌شود. این ترفند با تبدیل داده‌هایی که به صورت خطی جداپذیر نیستند، به داده‌هایی که در فضای بُعد بالاتر به صورت خطی جداپذیر باشند عمل میکند. تابع کرنل بر روی هر نمونه داده اعمال می‌شود تا نقاط داده اصلی و غیرخطی را به یک فضای بُعد بالاتر نگاشت دهد که در آن به صورت خطی جداپذیر باشند.