پیاده‌سازی رگرسیون چندجمله‌ ای با پایتون از پایه

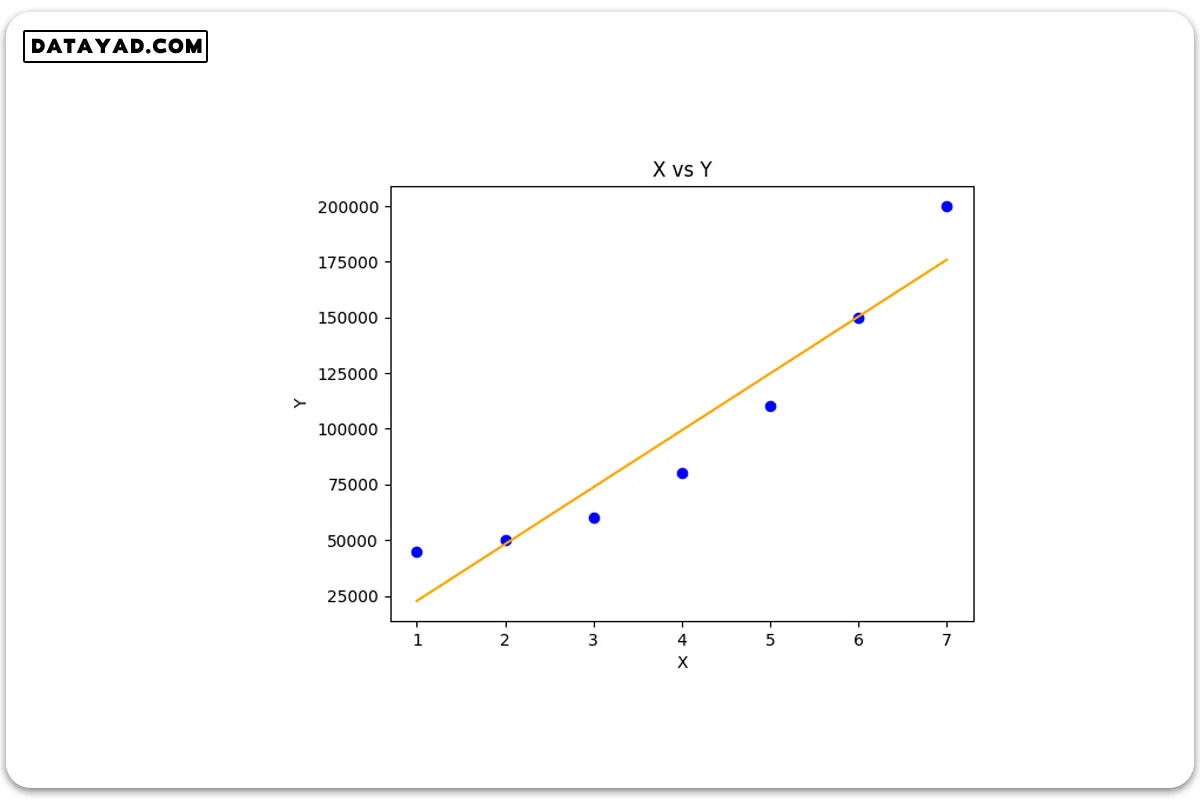
# Importing libraries

import numpy as np

import pandas as pd

from sklearn.model_selection import train_test_split

import matplotlib.pyplot as plt

from sklearn.linear_model import LinearRegression

# driver code

def main() :
	
	# Create dataset
	
	X = np.array( [ [1], [2], [3], [4], [5], [6], [7] ] )
	
	Y = np.array( [ 45000, 50000, 60000, 80000, 110000, 150000, 200000 ] )
	
	# Model training
	
	model = LinearRegression()

	model.fit( X, Y )
	
	# Prediction

	Y_pred = model.predict( X )
	
	# Visualization 
	
	plt.scatter( X, Y, color = 'blue' )
	
	plt.plot( X, Y_pred, color = 'orange' )
	
	plt.title( 'X vs Y' )
	
	plt.xlabel( 'X' )
	
	plt.ylabel( 'Y' )
	
	plt.show()
	
	
if __name__ == "__main__" : 
	
	main()

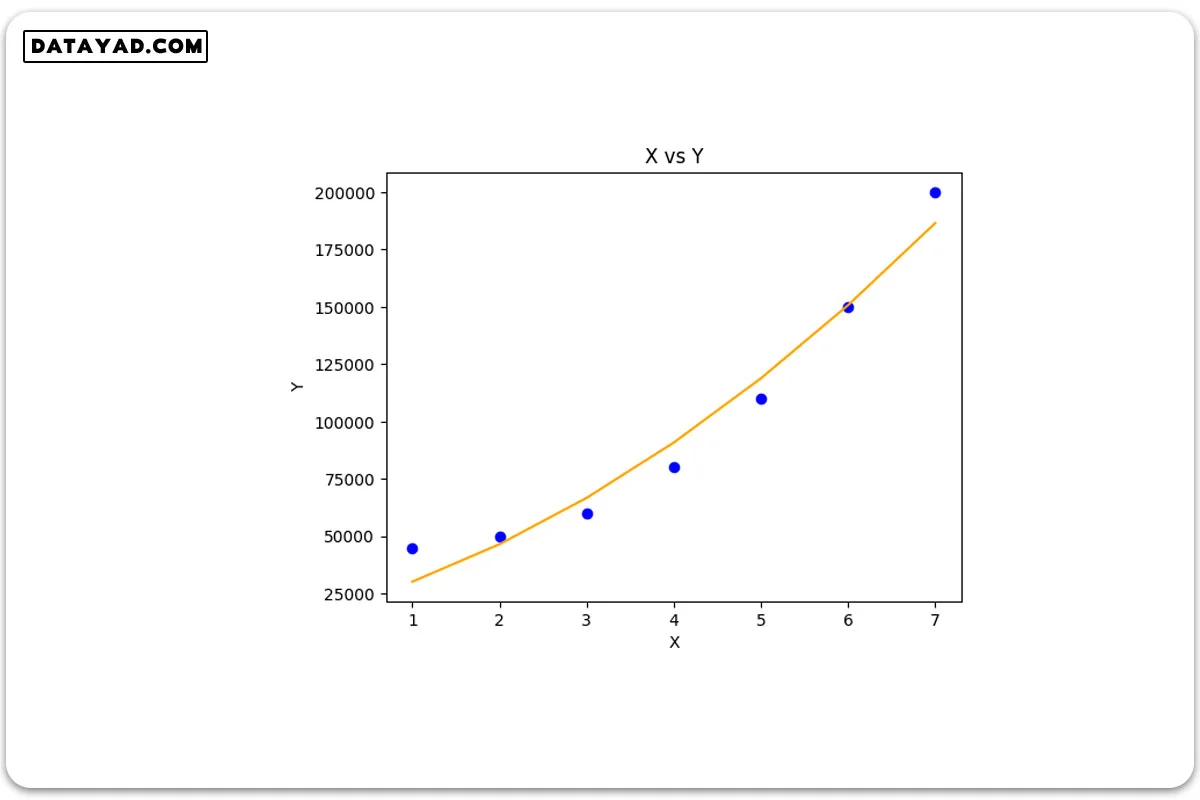
# Importing libraries

import numpy as np

import math

import matplotlib.pyplot as plt

# Univariate Polynomial Regression

class PolynomailRegression() :
	
	def __init__( self, degree, learning_rate, iterations ) :
		
		self.degree = degree
		
		self.learning_rate = learning_rate
		
		self.iterations = iterations
		
	# function to transform X
	
	def transform( self, X ) :
		
		# initialize X_transform
		
		X_transform = np.ones( ( self.m, 1 ) )
		
		j = 0
	
		for j in range( self.degree + 1 ) :
			
			if j != 0 :
				
				x_pow = np.power( X, j )
				
				# append x_pow to X_transform
				
				X_transform = np.append( X_transform, x_pow.reshape( -1, 1 ), axis = 1 )

		return X_transform 
	
	# function to normalize X_transform
	
	def normalize( self, X ) :
		
		X[:, 1:] = ( X[:, 1:] - np.mean( X[:, 1:], axis = 0 ) ) / np.std( X[:, 1:], axis = 0 )
		
		return X
		
	# model training
	
	def fit( self, X, Y ) :
		
		self.X = X
	
		self.Y = Y
	
		self.m, self.n = self.X.shape
	
		# weight initialization
	
		self.W = np.zeros( self.degree + 1 )
		
		# transform X for polynomial h( x ) = w0 * x^0 + w1 * x^1 + w2 * x^2 + ........+ wn * x^n
		
		X_transform = self.transform( self.X )
		
		# normalize X_transform
		
		X_normalize = self.normalize( X_transform )
				
		# gradient descent learning
	
		for i in range( self.iterations ) :
			
			h = self.predict( self.X )
		
			error = h - self.Y
			
			# update weights 
		
			self.W = self.W - self.learning_rate * ( 1 / self.m ) * np.dot( X_normalize.T, error ) 
		
		return self
	
	# predict 
	
	def predict( self, X ) :
	
		# transform X for polynomial h( x ) = w0 * x^0 + w1 * x^1 + w2 * x^2 + ........+ wn * x^n
		
		X_transform = self.transform( X )
		
		X_normalize = self.normalize( X_transform )
		
		return np.dot( X_transform, self.W )
	
	
# Driver code	 

def main() : 
	
	# Create dataset
	
	X = np.array( [ [1], [2], [3], [4], [5], [6], [7] ] )
	
	Y = np.array( [ 45000, 50000, 60000, 80000, 110000, 150000, 200000 ] )

	# model training
	
	model = PolynomailRegression( degree = 2, learning_rate = 0.01, iterations = 500 )

	model.fit( X, Y )
	
	# Prediction on training set

	Y_pred = model.predict( X )
	
	# Visualization 
	
	plt.scatter( X, Y, color = 'blue' )
	
	plt.plot( X, Y_pred, color = 'orange' )
	
	plt.title( 'X vs Y' )
	
	plt.xlabel( 'X' )
	
	plt.ylabel( 'Y' )
	
	plt.show()


if __name__ == "__main__" : 
	
	main()