رگرسیون خطی با کتابخانه sklearn

فهرست مطالب
رگرسیون خطی (Linear Regression)، یک روش یادگیری ماشین است که بر پایه یادگیری با نظارت فعالیت میکند. این روش برای انجام وظایف رگرسیونی به کار میرود. در مدلهای رگرسیون، مقدار پیشبینی شده بر اساس متغیرهای مستقل تعیین میشود. این مدلها بیشتر برای کشف روابط بین متغیرها و پیشبینی آینده کاربرد دارند.
انواع مختلف مدلهای رگرسیون بر اساس نوع رابطهای که بین متغیرهای وابسته و مستقل برقرار میکنند و تعداد متغیرهای مستقل به کار رفته، متفاوت هستند. در این مقاله، نحوه استفاده از کتابخانههای متفاوت پایتون از جمله sklearn برای پیادهسازی رگرسیون خطی روی دادههای مشخص شرح داده خواهد شد.
ما نمونهای از مدل خطی دوتایی را به نمایش خواهیم گذاشت که بصریسازی آن آسانتر است. در این نمونه، مدل برای یادگیری از روش گرادیان کاهشی استفاده خواهد کرد.
گام 1: وارد کردن تمام کتابخانههای مورد نیاز
import numpy as np import pandas as pd import seaborn as sns import matplotlib.pyplot as plt from sklearn import preprocessing, svm from sklearn.model_selection import train_test_split from sklearn.linear_model import LinearRegression
گام 2: خواندن مجموعه دادهها
میتوانید مجموعه دادهها را دانلود کنید.
df = pd.read_csv('bottle.csv')
df_binary = df[['Salnty', 'T_degC']]
# Taking only the selected two attributes from the dataset
df_binary.columns = ['Sal', 'Temp']
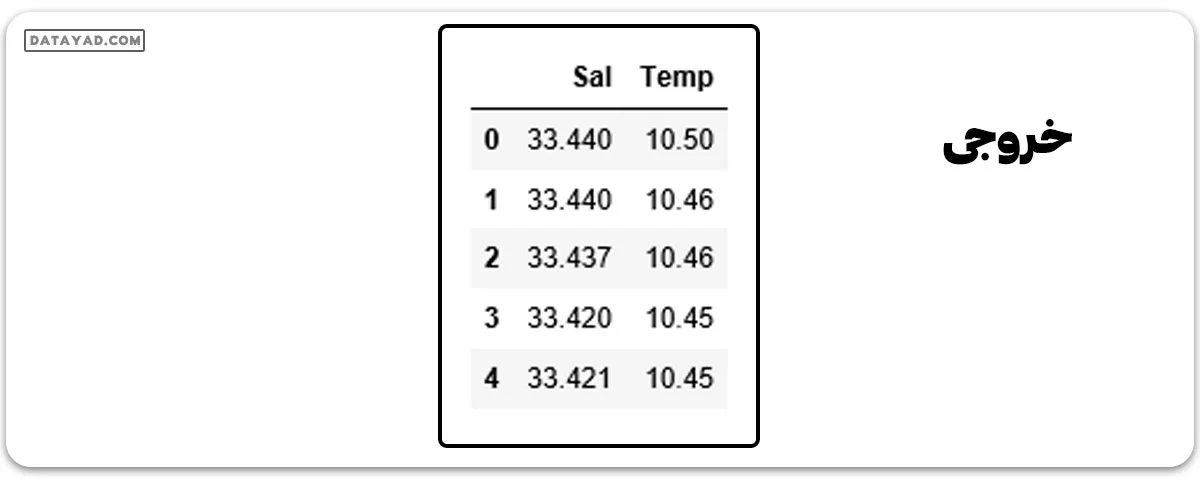
#display the first 5 rows
df_binary.head()
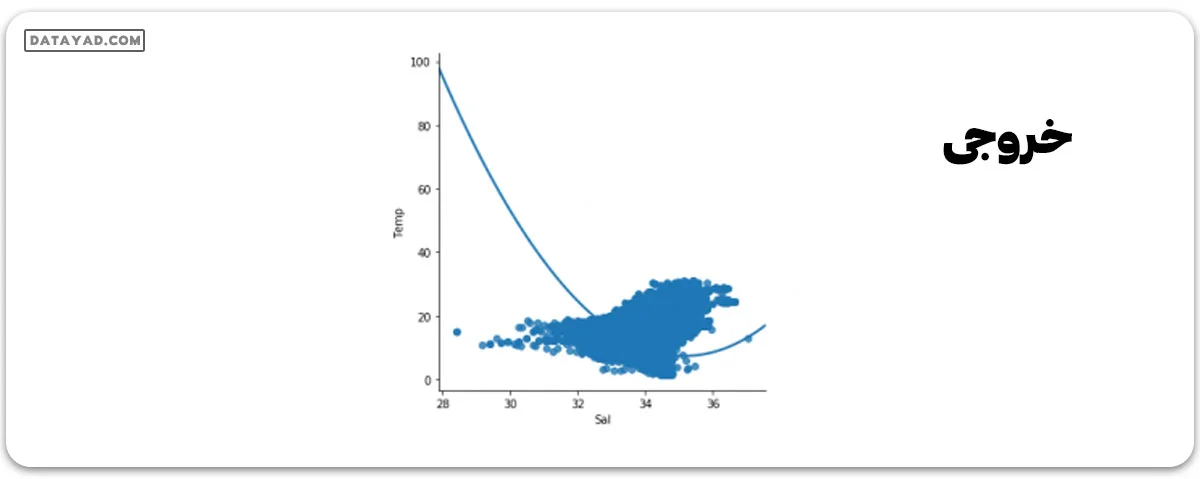
گام 3: بررسی پراکندگی دادهها
#plotting the Scatter plot to check relationship between Sal and Temp sns.lmplot(x ="Sal", y ="Temp", data = df_binary, order = 2, ci = None) plt.show()
گام 4: پاکسازی دادهها
# Eliminating NaN or missing input numbers df_binary.fillna(method ='ffill', inplace = True)
گام 5: آموزش مدل
X = np.array(df_binary['Sal']).reshape(-1, 1) y = np.array(df_binary['Temp']).reshape(-1, 1) # Separating the data into independent and dependent variables # Converting each dataframe into a numpy array # since each dataframe contains only one column df_binary.dropna(inplace = True) # Dropping any rows with Nan values X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25) # Splitting the data into training and testing data regr = LinearRegression() regr.fit(X_train, y_train) print(regr.score(X_test, y_test))
خروجی:
0.20780376990868232
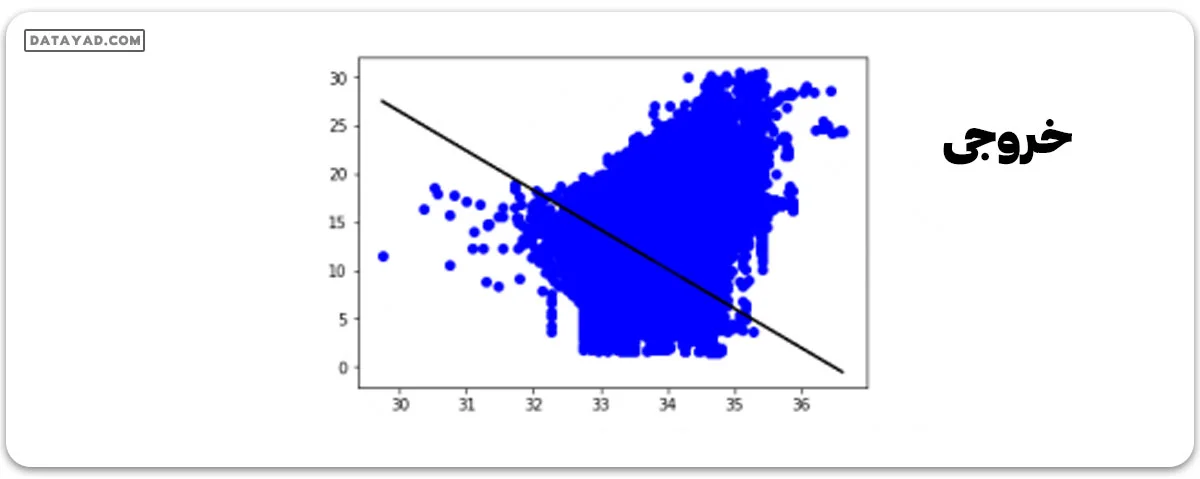
گام 6: بررسی نتایج حاصل شده
y_pred = regr.predict(X_test) plt.scatter(X_test, y_test, color ='b') plt.plot(X_test, y_pred, color ='k') plt.show() # Data scatter of predicted values
کم بودن دقت مدل ما نشاندهنده این است که مدل رگرسیونی ما به خوبی با دادههای موجود همخوانی ندارد. این موضوع به ما میگوید که دادههای ما برای رگرسیون خطی مناسب نیستند. با این حال، گاهی اوقات یک مجموعه داده میتواند یک رگرسیون خطی را بپذیرد اگر فقط بخشی از آن در نظر گرفته شود. بیایید این احتمال را بررسی کنیم.
گام 7: کار کردن با مجموعه دادهای کوچکتر
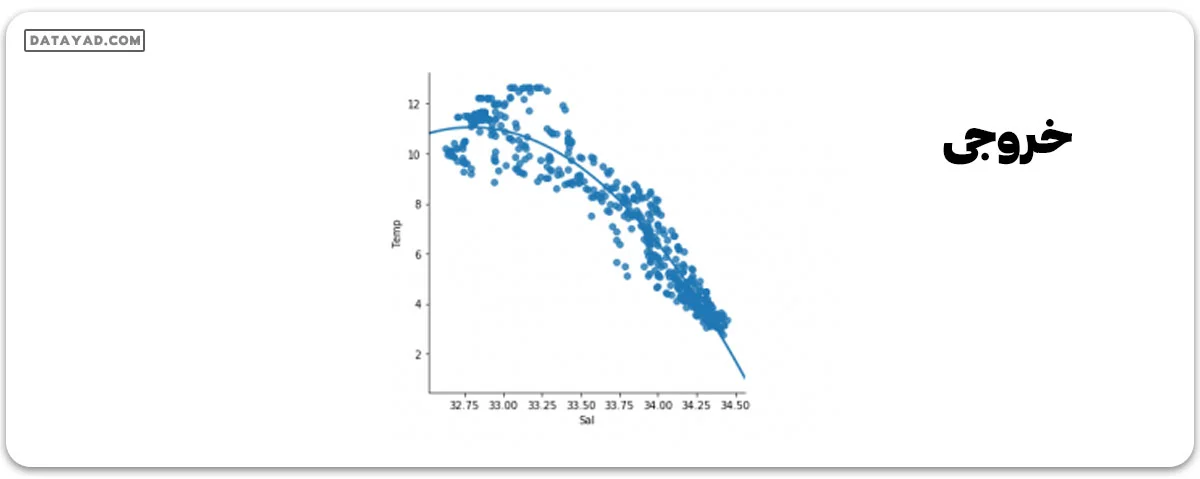
df_binary500 = df_binary[:][:500] # Selecting the 1st 500 rows of the data sns.lmplot(x ="Sal", y ="Temp", data = df_binary500, order = 2, ci = None)
ما متوجه میشویم که 500 سطر اولیه دادهها از یک مدل خطی پیروی میکنند.
ما همین مراحل قبلی را ادامه میدهیم.
df_binary500.fillna(method ='fill', inplace = True) X = np.array(df_binary500['Sal']).reshape(-1, 1) y = np.array(df_binary500['Temp']).reshape(-1, 1) df_binary500.dropna(inplace = True) X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25) regr = LinearRegression() regr.fit(X_train, y_train) print(regr.score(X_test, y_test))
خروجی:
0.847594139663558
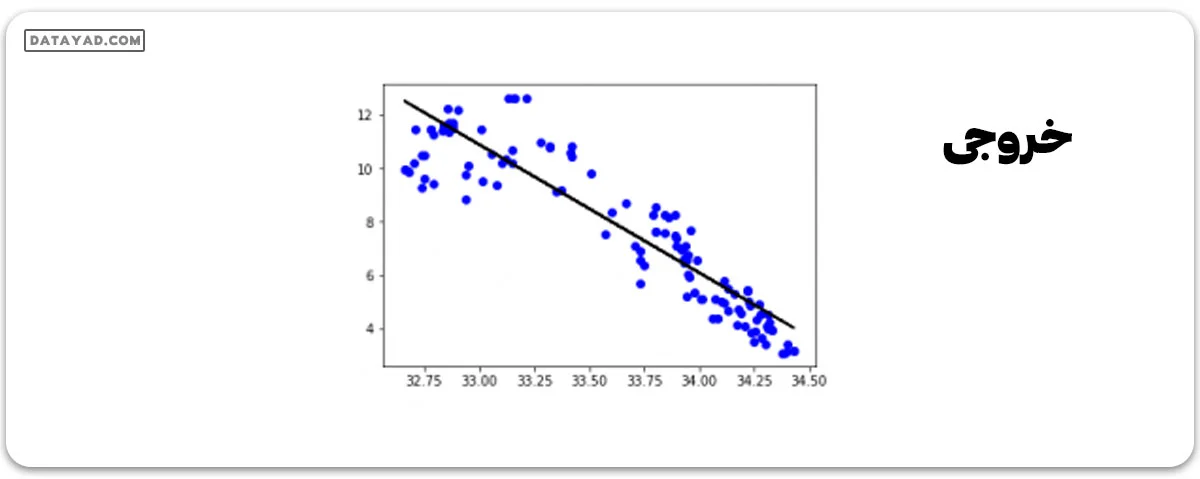
y_pred = regr.predict(X_test) plt.scatter(X_test, y_test, color ='b') plt.plot(X_test, y_pred, color ='k') plt.show()
گام 8: معیارهای ارزیابی برای رگرسیون
در انتها، ما عملکرد مدل رگرسیون خطی در یادگیری ماشین را با استفاده از معیارهای ارزیابی مورد بررسی قرار میدهیم. برای الگوریتمهای رگرسیون، معمولاً از معیارهای خطای مطلق میانگین و خطای مربع میانگین برای سنجش عملکرد مدل استفاده میشود.
from sklearn.metrics import mean_absolute_error,mean_squared_error
mae = mean_absolute_error(y_true=y_test,y_pred=y_pred)
#squared True returns MSE value, False returns RMSE value.
mse = mean_squared_error(y_true=y_test,y_pred=y_pred) #default=True
rmse = mean_squared_error(y_true=y_test,y_pred=y_pred,squared=False)
print("MAE:",mae)
print("MSE:",mse)
print("RMSE:",rmse)
خروجی:
MAE: 0.7927322046360309 MSE: 1.0251137190180517 RMSE: 1.0124789968281078