رگرسیون خطی چندگانه در پایتون

فهرست مطالب
در درس بیست و دوم از آموزش رایگان یادگیری ماشین با پایتون می خواهیم در مورد رگرسیون خطی چندگانه (Multiple Linear Regression using Python) صحبت کنیم.
در دنیای امروز که دادهها به یکی از مهمترین منابع برای تصمیمگیری در حوزههای مختلف تبدیل شدهاند، استفاده از ابزارهای تحلیل آماری پیشرفته بیش از پیش اهمیت یافته است. یکی از این ابزارهای قدرتمند، رگرسیون خطی چند متغیره است که به ما کمک میکند تا روابط پیچیده بین متغیرها را درک کرده و پیشبینیهای دقیقی انجام دهیم. این روش، بهویژه در تجزیه و تحلیل متغیرها، نقش کلیدی دارد و در بسیاری از زمینهها از اقتصاد گرفته تا علوم پزشکی و اجتماعی کاربرد گستردهای دارد.
در ادامه، قصد داریم شما را با تمامی جنبههای رگرسیون خطی چند متغیره آشنا کنیم؛ از مفاهیم پایه و کاربردها گرفته تا روشهای برآورد پارامترها، ارزیابی مدل، مشکلات متداول و تکنیکهای بهبود آن. همچنین، به صورت عملی نشان خواهیم داد که چگونه میتوانید این مدل را در پایتون پیادهسازی کنید. برای درک بهتر تفاوتهای بین رگرسیون خطی ساده و رگرسیون خطی چند متغیره، جدول زیر را بررسی کنید:
| ویژگی | رگرسیون خطی ساده | رگرسیون خطی چند متغیره |
| تعداد متغیرهای مستقل | 1 | 2 یا بیشتر |
| معادله مدل | y=β0+β1x+ϵ y = \beta_0 + \beta_1 x + \epsilon y=β0+β1x+ϵ | y=β0+β1×1+β2×2+⋯+βkxk+ϵ y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \dots + \beta_k x_k + \epsilon y=β0+β1x1+β2x2+⋯+βkxk+ϵ |
| پیچیدگی مدل | ساده | پیچیدهتر به دلیل وجود متغیرهای بیشتر |
| کاربردها | تحلیل روابط ساده | تحلیل روابط پیچیده و چندمتغیره |
| تفسیر ضرایب | آسان | نیاز به دقت بیشتر به دلیل تعامل متغیرها |
این جدول نشان میدهد که رگرسیون خطی چند متغیره ابزاری مناسب برای تحلیلهای پیشرفتهتر و جامعتر است و توانایی مدلسازی روابط پیچیدهتر را دارد.
تفاوت رگرسیون خطی چند متغیره با رگرسیون خطی ساده
رگرسیون خطی ساده و رگرسیون خطی چند متغیره هر دو ابزارهای مهمی در تحلیل آماری هستند، اما تفاوتهای کلیدی بین آنها وجود دارد که در جدول بالا به آن اشاره کردیم. در رگرسیون خطی ساده، تنها یک متغیر مستقل برای پیش بینی متغیر وابسته استفاده میشود. به عنوان مثال، اگر بخواهیم تاثیر مساحت خانه بر قیمت آن را بررسی کنیم، از رگرسیون خطی ساده استفاده میکنیم. معادله آن به صورت y=β0+β1x+ϵ y = \beta_0 + \beta_1 x + \epsilon y=β0+β1x+ϵ است که در آن y y y متغیر وابسته، x x x متغیر مستقل و ϵ \epsilon ϵ خطا است.
اما در رگرسیون خطی چند متغیره، چندین متغیر مستقل به طور همزمان در نظر گرفته میشوند. مثلاً برای پیش بینی قیمت خانه، میتوانیم علاوه بر مساحت، تعداد اتاقها، سن بنا و موقعیت جغرافیایی را نیز به مدل اضافه کنیم. معادله این مدل به صورت y=β0+β1×1+β2×2+⋯+βkxk+ϵ y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \dots + \beta_k x_k + \epsilon y=β0+β1x1+β2x2+⋯+βkxk+ϵ است. این پیچیدگی باعث میشود که رگرسیون خطی چند متغیره برای تحلیلهای پیشرفتهتر و واقعیتر مناسب باشد، اما در عین حال چالشهایی مانند تفسیر ضرایب و مدیریت تعامل بین متغیرها را به همراه دارد.
رگرسیون خطی
روشی پایهای و رایج برای تجزیه و تحلیل پیشبینی است. رگرسیون خطی به معنای استفاده از روشهای آماری برای بررسی و مدلسازی ارتباط بین یک متغیر وابسته و گروهی از متغیرهای مستقل است.
این مدلها به دو دسته تقسیم میشوند:
1- رگرسیون خطی تک متغیره یا ساده
2- رگرسیون خطی چندگانه
بیایید درباره استفاده از رگرسیون خطی چندگانه با پایتون صحبت کنیم.
رگرسیون خطی چندگانه سعی میکند تا رابطه بین دو یا چند متغیر مستقل و یک پاسخ را با قرار دادن یک معادله خطی بر روی دادههای موجود، مدلسازی نماید. گامهای انجام این نوع رگرسیون تقریباً مشابه رگرسیون خطی ساده است، اما تفاوت در ارزیابی آنهاست. میتوان از این روش برای درک اینکه کدام عامل، بیشترین تأثیر را بر خروجی پیشبینی شده دارد و چگونه متغیرهای مختلف با یکدیگر در ارتباط هستند، استفاده کرد.
در این مدل، Y به صورت زیر بیان میشود:
Y = b0 + b1 * x1 + b2 * x2 + b3 * x3 + …… bn * xn
که در آن، Y متغیر وابسته و x1, x2, x3, …… xn متغیرهای مستقل چندگانهای هستند که در نظر گرفته میشوند.
کاربردها
رگرسیون خطی چند متغیره در بسیاری از حوزهها کاربرد دارد و به ما امکان میدهد تا تاثیر چندین متغیر را به طور همزمان بر یک متغیر وابسته بررسی کنیم. در ادامه به برخی از مهمترین کاربردهای این روش در تجزیه و تحلیل متغیرها اشاره میکنیم:
- اقتصاد: از رگرسیون خطی چند متغیره برای پیشبینی رشد اقتصادی بر اساس متغیرهایی مانند نرخ بهره، تورم، سرمایهگذاری و تولید ناخالص داخلی استفاده میشود. به عنوان مثال، یک اقتصاددان میتواند با این روش پیشبینی کند که چگونه تغییرات در سیاستهای مالی بر رشد اقتصادی تاثیر میگذارد.
- پزشکی: در این حوزه، رگرسیون خطی چند متغیره برای تحلیل تاثیر عوامل مختلف مانند سن، وزن، فشار خون و سابقه خانوادگی بر احتمال ابتلا به بیماریهایی مانند دیابت یا بیماریهای قلبی به کار میرود. این روش به پزشکان کمک میکند تا عوامل خطر را شناسایی کرده و برنامههای درمانی بهتری طراحی کنند.
- علوم اجتماعی: پژوهشگران از این روش برای بررسی تاثیر متغیرهایی مانند تحصیلات، درآمد، جنسیت و سن بر رفتارهای اجتماعی مانند رایدهی یا میزان رضایت از زندگی استفاده میکنند. این تحلیلها به درک بهتر الگوهای اجتماعی کمک میکند.
- بازاریابی: در این حوزه، رگرسیون خطی چند متغیره برای پیشبینی فروش بر اساس متغیرهایی مانند بودجه تبلیغات، قیمت محصول، فصل و ترجیحات مشتریان به کار میرود. این اطلاعات به شرکتها کمک میکند تا استراتژیهای بازاریابی خود را بهینه کنند.
به نقل از University of Virginia Library : “رگرسیون چند متغیره به شما امکان میدهد تا روابط پیچیده بین متغیرها را درک کنید و پیشبینیهای دقیقتری انجام دهید.” این نقل قول نشان دهنده اهمیت این روش در تحلیل آماری است.
فرضیات اصلی مدل رگرسیون
- خطی بودن: رابطه میان متغیرهای وابسته و مستقل باید حالت خطی داشته باشد.
- همسانی واریانس: تغییرات خطاها باید ثابت باقی بمانند.
- نرمالیته چندمتغیری: رگرسیون چندگانه بر این فرض استوار است که باقیماندهها دارای توزیع نرمال هستند.
- نبود چندخطیگرایی: این مدل فرض میکند که در دادهها چندخطیگرایی به میزان کم بوده یا اصلاً وجود ندارد.
روشهای برآورد پارامترها
برای ساخت یک مدل رگرسیون خطی چند متغیره، ابتدا باید ضرایب یا پارامترهای مدل (مانند β0,β1,…,βk \beta_0, \beta_1, \dots, \beta_k β0,β1,…,βk) را برآورد کنیم. دو روش اصلی برای این کار وجود دارد که در ادامه توضیح داده میشوند:
روش کمترین مربعات معمولی (OLS)
روش کمترین مربعات معمولی (Ordinary Least Squares OLS) یکی از رایجترین روشها برای برآورد پارامترها در رگرسیون خطی چند متغیره است. در این روش، هدف کمینه کردن مجموع مربعات خطاها (تفاوت بین مقادیر واقعی و مقادیر پیشبینیشده) است. به عبارت دیگر، ضرایب به گونهای انتخاب میشوند که خط رگرسیون بهترین تطابق را با دادهها داشته باشد.
مزایای OLS شامل سادگی محاسباتی و عدم نیاز به فرضهای پیچیده در مورد توزیع دادهها است (به جز فرض خطی بودن رابطه و استقلال خطاها). این روش در بسیاری از نرمافزارهای آماری مانند پایتون و R به صورت پیشفرض استفاده میشود.
روش حداکثر درست نمایی (Maximum Likelihood)
روش حداکثر درست نمایی (Maximum Likelihood Estimation MLE) رویکرد دیگری برای برآورد پارامترها است که بر اساس فرض نرمال بودن خطاها عمل میکند. در این روش، ضرایب به گونهای انتخاب میشوند که احتمال مشاهده دادههای موجود تحت مدل پیشنهادی بیشینه شود. این روش در شرایطی که دادهها نرمال باشند، نتایجی مشابه OLS ارائه میدهد، اما در مدلهای پیچیدهتر یا با فرضهای خاص، انعطافپذیری بیشتری دارد. هر دو روش در تحلیل آماری کاربرد دارند و انتخاب بین آنها به نوع دادهها و فرضهای مدل بستگی دارد.
تکنیکهای بهبود مدل
برای افزایش دقت و کارایی مدل رگرسیون خطی چند متغیره، میتوان از تکنیکهای زیر استفاده کرد:
انتخاب متغیرهای مؤثر
انتخاب متغیرهای مناسب یکی از مهمترین مراحل در ساخت مدل است. متغیرهای غیرضروری میتوانند باعث پیچیدگی غیرضروری و کاهش دقت مدل شوند. روشهایی مانند انتخاب پیشرو (Forward Selection)، که در آن متغیرها یکییکی به مدل اضافه میشوند، یا انتخاب پسرو (Backward Elimination)، که در آن متغیرهای غیرمعنادار حذف میشوند، برای این منظور استفاده میشوند.
استفاده از روشهای تنظیم (Regularization)
روشهای تنظیم مانند ریج (Ridge Regression) و لاسو (Lasso Regression) به جلوگیری از بیشبرازش (Overfitting) کمک میکنند. این روشها با افزودن یک جریمه به ضرایب بزرگ، مدل را سادهتر کرده و در مواردی که چندخطیگرایی وجود دارد، عملکرد بهتری ارائه میدهند.
تبدیل متغیرها برای بهبود نرمالیته
یکی از فرضهای رگرسیون خطی، نرمال بودن خطاها است. اگر دادهها یا خطاها نرمال نباشند، میتوان از تبدیلهایی مانند لگاریتم، ریشه دوم یا معکوس استفاده کرد تا توزیع دادهها به نرمال نزدیکتر شود. این کار باعث بهبود دقت پیشبینیها و پایداری مدل میشود.
متغیرهای موهومی (Dummy Variable)
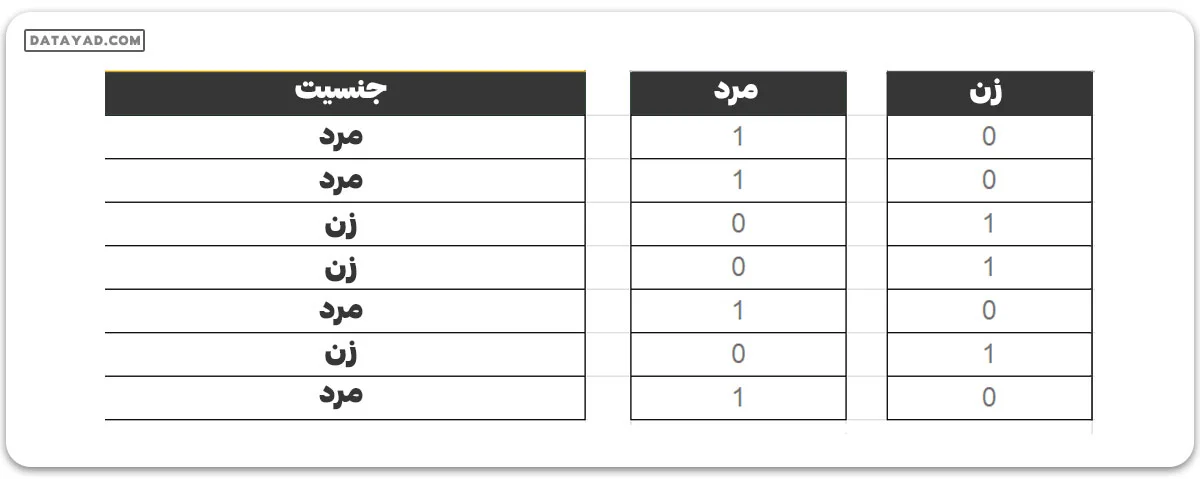
همانطور که میدانیم، در مدل رگرسیون چندگانه از دادههای دستهبندی شده زیادی استفاده میشود. بهکارگیری دادههای دستهبندی شده روش خوبی برای دربرگرفتن دادههای غیرعددی در مدل رگرسیون مربوطه است.
دادههای دستهبندی شده به مقادیری اشاره دارند که دستهها را نشان میدهند، مقادیری با تعداد ثابت و غیرمرتب، مثل جنسیت (مرد/زن). در مدل رگرسیون، این مقادیر میتوانند توسط متغیرهای موهومی نمایش داده شوند.
این متغیرها شامل مقادیری مانند ۰ یا ۱ هستند که وجود و عدم وجود مقادیر دستهبندی شده را نشان میدهند.
تله متغیر موهومی
تله متغیر موهومی شرایطی است که در آن دو یا چند متغیر به شدت با هم ارتباط دارند. به بیان ساده، میتوان گفت که یک متغیر میتواند از پیشبینی متغیر دیگر حدس زده شود. راهحل برای خروج از این تله این است که یکی از متغیرهای دستهبندی را حذف کنیم. پس اگر m متغیر موهوم وجود داشته باشد، در مدل از m-1 متغیر استفاده میشود.
D2 = D1 – 1
در اینجا D2, D1 متغیرهای موهوم هستند.
روشهای ساخت مدلها
– همهجانبه (All-in)
– حذف عقبگرد (Backward-Elimination)
– انتخاب روبه جلو (Forward Selection)
– حذف دوجانبه (Bidirectional Elimination)
– مقایسه امتیاز (Score Comparison)
روش حذف عقبگرد
گام اول: ابتدا یک سطح معناداری برای شروع مدل انتخاب کنید.
گام دوم: مدل کامل را با در نظر گرفتن تمامی پیشبینهای ممکن، بسازید.
گام سوم: پیشبینیکننده با بالاترین مقدار P را بررسی کنید. اگر P بیشتر از سطح معناداری (SL) باشد، به گام چهارم بروید؛ در غیر این صورت، مدل آماده است.
گام چهارم: این پیشبینیکننده را از مدل حذف کنید.
گام پنجم: مدل را بدون این متغیر مجدداً تنظیم کنید.
روش انتخاب روبه جلو
گام اول: یک سطح معناداری برای ورود به مدل تعیین کنید (مثلاً SL = 0.05).
گام دوم: تمام مدلهای رگرسیون ساده y~ x(n) را آزمایش کنید و مدلی را که کمترین مقدار P را دارد، انتخاب کنید.
گام سوم: این متغیر را حفظ کرده و تمام مدلهای ممکن را با اضافه کردن یک پیشبینیکننده دیگر به آنچه در حال حاضر دارید، امتحان کنید.
گام چهارم: پیشبینیکنندهای که کمترین مقدار P را دارد را در نظر بگیرید. اگر P کمتر از SL باشد، به گام سوم بازگردید؛ در غیر این صورت، مدل آماده است.
گامهای مورد نیاز در هر مدل رگرسیون خطی چندگانه
گام اول: آمادهسازی دادهها
- بارگذاری کتابخانههای مورد نیاز.
- وارد کردن مجموعه دادهها.
- رمزگذاری دادههای دستهای.
- اجتناب از تله متغیرهای موهوم.
- تقسیم مجموعه داده به بخشهای آموزشی و تست.
گام دوم: اعمال مدل رگرسیون خطی چندگانه روی مجموعه آموزشی
گام سوم: پیشبینی نتایج بر اساس مجموعه دادههای تست.
کد 1:
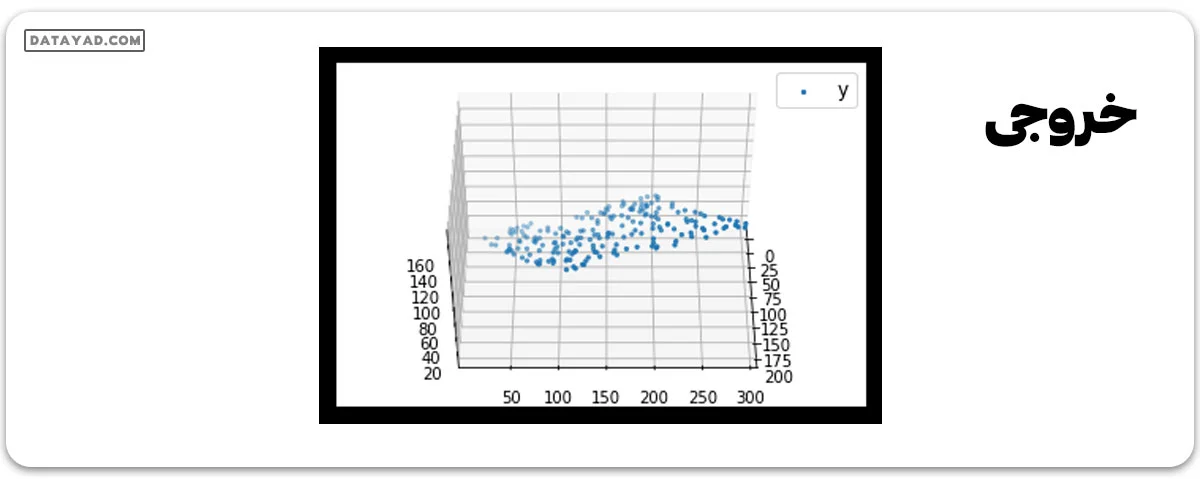
import numpy as np import matplotlib as mpl from mpl_toolkits.mplot3d import Axes3D import matplotlib.pyplot as plt def generate_dataset(n): x = [] y = [] random_x1 = np.random.rand() random_x2 = np.random.rand() for i in range(n): x1 = i x2 = i/2 + np.random.rand()*n x.append([1, x1, x2]) y.append(random_x1 * x1 + random_x2 * x2 + 1) return np.array(x), np.array(y) x, y = generate_dataset(200) mpl.rcParams['legend.fontsize'] = 12 fig = plt.figure() ax = fig.add_subplot(projection ='3d') ax.scatter(x[:, 1], x[:, 2], y, label ='y', s = 5) ax.legend() ax.view_init(45, 0) plt.show()
کد 2:
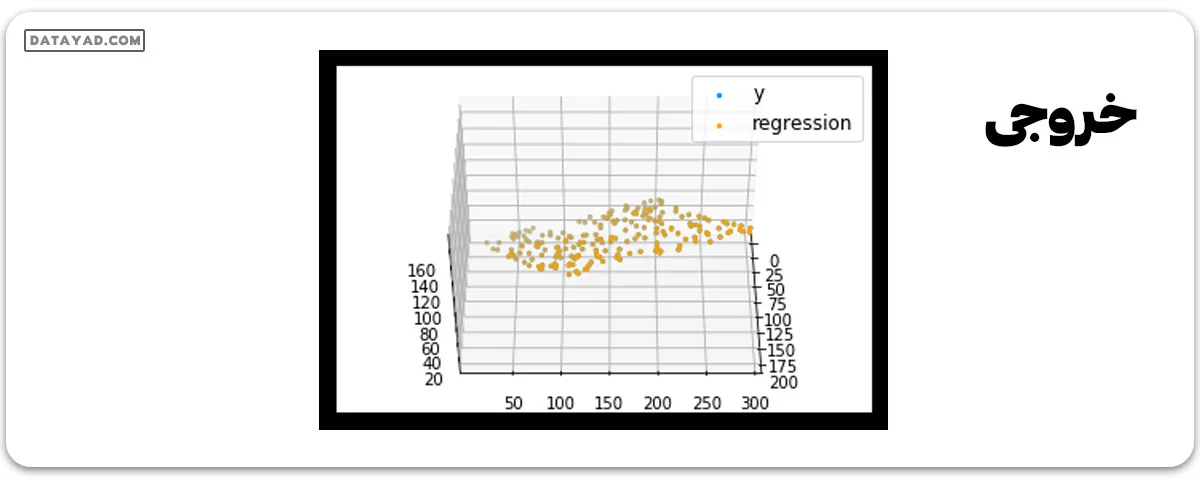
def mse(coef, x, y): return np.mean((np.dot(x, coef) - y)**2)/2 def gradients(coef, x, y): return np.mean(x.transpose()*(np.dot(x, coef) - y), axis=1) def multilinear_regression(coef, x, y, lr, b1=0.9, b2=0.999, epsilon=1e-8): prev_error = 0 m_coef = np.zeros(coef.shape) v_coef = np.zeros(coef.shape) moment_m_coef = np.zeros(coef.shape) moment_v_coef = np.zeros(coef.shape) t = 0 while True: error = mse(coef, x, y) if abs(error - prev_error) <= epsilon: break prev_error = error grad = gradients(coef, x, y) t += 1 m_coef = b1 * m_coef + (1-b1)*grad v_coef = b2 * v_coef + (1-b2)*grad**2 moment_m_coef = m_coef / (1-b1**t) moment_v_coef = v_coef / (1-b2**t) delta = ((lr / moment_v_coef**0.5 + 1e-8) * (b1 * moment_m_coef + (1-b1)*grad/(1-b1**t))) coef = np.subtract(coef, delta) return coef coef = np.array([0, 0, 0]) c = multilinear_regression(coef, x, y, 1e-1) fig = plt.figure() ax = fig.add_subplot(projection='3d') ax.scatter(x[:, 1], x[:, 2], y, label='y', s=5, color="dodgerblue") ax.scatter(x[:, 1], x[:, 2], c[0] + c[1]*x[:, 1] + c[2]*x[:, 2], label='regression', s=5, color="orange") ax.view_init(45, 0) ax.legend() plt.show()
رگرسیون خطی چندگانه یک تکنیک آماری است که برای بررسی ارتباط بین چند متغیر مستقل و یک متغیر وابسته به کار میرود. در پایتون، کتابخانه scikit-learn یک اجرای راحت از رگرسیون خطی چندگانه را از طریق کلاس LinearRegression ارائه میدهد. در اینجا یک نمونه برای نحوه استفاده از LinearRegression برای ساخت یک مدل رگرسیون خطی چندگانه در پایتون آورده شده است:
from sklearn.linear_model import LinearRegression import numpy as np # Assume you have independent variables X and a dependent variable y X = np.array([[1, 2, 3], [2, 3, 4], [3, 4, 5], [4, 5, 6]]) y = np.array([1, 2, 3, 4]) # Create an instance of the LinearRegression class reg = LinearRegression() # Fit the model to the data reg.fit(X, y) # Print the coefficients of the model print(reg.coef_)
این فرآیند به ما ضرایب مدل رگرسیون خطی چندگانه را میدهد که برای پیشبینی متغیر وابسته بر اساس مقادیر جدید متغیرهای مستقل قابل استفاده هستند.
این نکته مهم است که مدل رگرسیون خطی (و همچنین رگرسیون لجستیک ) باید با توجه به فرضیات خاصی مانند خطی بودن، همسانی واریانس، استقلال خطاها، نرمالیته خطاها و نبود چندخطیگرایی به کار رود. اگر این فرضیات برآورده نشوند، باید به فکر استفاده از روشهای دیگر یا تغییر دادن دادهها باشید.
ارزیابی مدل رگرسیون
پس از برآورد پارامترها، باید کیفیت مدل رگرسیون خطی چند متغیره را ارزیابی کنیم تا مطمئن شویم که پیشبینیهای آن قابل اعتماد هستند. معیارها و آزمونهای زیر برای این منظور استفاده میشوند:
ضریب تعیین (R²) و تفسیر آن
ضریب تعیین (R²) یکی از مهمترین معیارها برای ارزیابی مدل است. این معیار نشان میدهد که چه درصدی از واریانس متغیر وابسته توسط متغیرهای مستقل توضیح داده میشود. مقادیر R² بین 0 و 1 قرار دارند؛ هرچه مقدار آن به 1 نزدیکتر باشد، مدل توانایی بیشتری در توضیح دادهها دارد. به عنوان مثال، اگر R² برابر 0.85 باشد، یعنی 85 درصد از تغییرات متغیر وابسته توسط مدل توضیح داده شده است.
آزمون معناداری کلی مدل (آزمون F)
آزمون F برای بررسی معناداری کلی مدل استفاده میشود. این آزمون فرضیه صفر را آزمایش میکند که همه ضرایب رگرسیون برابر صفر هستند. اگر مقدار p-value آزمون F کمتر از 0.05 باشد، میتوان نتیجه گرفت که مدل به طور کلی معنادار است و حداقل یکی از متغیرهای مستقل تاثیر قابل توجهی بر متغیر وابسته دارد.
بررسی معناداری ضرایب رگرسیون (آزمون t)
آزمون t برای هر ضریب رگرسیون به صورت جداگانه انجام میشود تا مشخص شود آیا آن ضریب از نظر آماری معنادار است یا خیر. فرضیه صفر در این آزمون این است که ضریب برابر صفر است. اگر p-value کمتر از 0.05 باشد، میتوان نتیجه گرفت که متغیر مربوطه تاثیر معناداری بر متغیر وابسته دارد. این آزمون به ما کمک میکند تا متغیرهای مهم را در مدل شناسایی کنیم.
مشکلات متداول در رگرسیون خطی چند متغیره
استفاده از رگرسیون خطی چند متغیره همیشه بدون چالش نیست. در ادامه به برخی از مشکلات رایج و راهحلهای آنها در تجزیه و تحلیل متغیرها اشاره میکنیم:
چندخطیگرایی (Multicollinearity)
چندخطیگرایی زمانی رخ میدهد که دو یا چند متغیر مستقل در مدل با یکدیگر همبستگی بالایی داشته باشند. این مشکل باعث میشود که برآورد ضرایب ناپایدار شده و تفسیر آنها دشوار شود. برای تشخیص چندخطیگرایی، میتوان از شاخص تورم واریانس (Variance Inflation Factor VIF) استفاده کرد. اگر VIF یک متغیر بیشتر از 10 باشد، نشاندهنده وجود چندخطیگرایی است. راهحلهایی مانند حذف متغیرهای همبسته یا ترکیب آنها میتواند این مشکل را برطرف کند.
خودهمبستگی (Autocorrelation)
خودهمبستگی زمانی رخ میدهد که خطاهای مدل با یکدیگر همبستگی داشته باشند، که معمولاً در دادههای سری زمانی دیده میشود. این مشکل میتواند باعث شود که برآوردهای ضرایب غیرقابل اعتماد شوند. برای تشخیص خودهمبستگی، از آزمون دوربین-واتسون (Durbin-Watson) استفاده میشود. مقادیر نزدیک به 2 نشاندهنده عدم وجود خودهمبستگی است، در حالی که مقادیر نزدیک به 0 یا 4 نشاندهنده وجود مشکل هستند. برای رفع این مشکل، میتوان از مدلهای سری زمانی مانند ARIMA استفاده کرد.
ناهمسانی واریانسها (Heteroscedasticity)
ناهمسانی واریانسها زمانی رخ میدهد که واریانس خطاها در طول دادهها یکسان نباشد. این مشکل میتواند دقت برآورد ضرایب را کاهش دهد. برای تشخیص آن، میتوان از آزمون بروش-پاگان (Breusch-Pagan) استفاده کرد. در صورت وجود ناهمسانی واریانسها، روشهایی مانند تبدیل متغیرها (مثلاً استفاده از لگاریتم) یا رگرسیون وزنی (Weighted Least Squares) میتواند به بهبود مدل کمک کند.
پیادهسازی رگرسیون خطی چند متغیره در پایتون
پایتون به دلیل داشتن کتابخانههای قدرتمند مانند Scikit-learn و Statsmodels، یکی از بهترین ابزارها برای پیادهسازی رگرسیون خطی چند متغیره است. در ادامه، یک مثال عملی از پیادهسازی این مدل ارائه میدهیم:
# وارد کردن کتابخانهها
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
# بارگذاری دادهها
data = pd.read_csv('data.csv') # فایل دادههای شما
X = data[['feature1', 'feature2', 'feature3']] # متغیرهای مستقل
y = data['target'] # متغیر وابسته
# تقسیم دادهها به مجموعه آموزش و آزمون
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# ایجاد و آموزش مدل
model = LinearRegression()
model.fit(X_train, y_train)
# پیشبینی و ارزیابی
y_pred = model.predict(X_test)
print('ضریب تعیین (R²):', r2_score(y_test, y_pred))
print('ضرایب رگرسیون:', model.coef_)
print('عرض از مبدا:', model.intercept_)
توضیح کد:
- وارد کردن دادهها: دادهها از یک فایل CSV بارگذاری میشوند. متغیرهای مستقل (X) و وابسته (y) مشخص میشوند.
- تقسیم دادهها: دادهها به دو بخش آموزش (80%) و آزمون (20%) تقسیم میشوند.
- ایجاد مدل: از کلاس LinearRegression برای ساخت مدل استفاده میشود.
- آموزش و پیشبینی: مدل با دادههای آموزشی آموزش داده شده و سپس برای پیشبینی دادههای آزمون استفاده میشود.
- ارزیابی: با استفاده از R²، کیفیت مدل ارزیابی میشود.
این کد یک نقطه شروع عالی برای پیادهسازی رگرسیون خطی چند متغیره در پروژههای تحلیل آماری است. برای یادگیری بیشتر، به آموزش رایگان یادگیری ماشین با پایتون مراجعه کنید.
رگرسیون خطی چند متغیره ابزاری قدرتمند در تحلیل آماری و تجزیه و تحلیل متغیرها است که به شما امکان میدهد روابط پیچیده بین متغیرها را مدلسازی کرده و پیشبینیهای دقیقی انجام دهید. از کاربردهای گسترده آن در اقتصاد، پزشکی و بازاریابی گرفته تا روشهای برآورد پارامترها و تکنیکهای بهبود مدل، این روش به شما کمک میکند تا از دادههای خود به بهترین شکل استفاده کنید. اگر میخواهید مهارت خود را در تحلیل دادهها تقویت کنید، دورههای آموزشی جامع دیتایاد را بررسی کنید! 🚀 مشاهده دورهها
سوالات متداول
1-آیا میتوان از رگرسیون خطی چند متغیره برای پیشبینی قیمت خانه استفاده کرد؟
بله، این روش یکی از ابزارهای رایج برای پیشبینی قیمت خانه است. با استفاده از متغیرهایی مانند مساحت، تعداد اتاقها، موقعیت جغرافیایی و سن بنا، میتوانید مدل دقیقی برای پیشبینی قیمت بسازید.
2-چگونه از رگرسیون چند متغیره در تحلیل دادههای پزشکی استفاده میشود؟
در پزشکی، رگرسیون خطی چند متغیره برای بررسی تاثیر همزمان چندین عامل (مانند سن، وزن، فشار خون و سابقه خانوادگی) بر احتمال ابتلا به بیماری یا پاسخ به درمان استفاده میشود. این روش به شناسایی عوامل کلیدی و بهبود تصمیمگیری کمک میکند.
3-کدام نرمافزارها برای اجرای رگرسیون خطی چند متغیره مناسبتر هستند؟
نرمافزارهایی مانند پایتون (Scikit-learn Statsmodels)، R، SPSS و SAS ابزارهای قدرتمندی برای اجرای این مدل هستند. پایتون به دلیل انعطافپذیری و جامعه بزرگ توسعهدهندگان، انتخاب محبوبی است.
4-چگونه دادهها را برای اجرای رگرسیون چند متغیره آماده کنیم؟
دادهها باید تمیز و بدون مقادیر گمشده باشند. متغیرهای مستقل نباید همبستگی بالایی داشته باشند (برای جلوگیری از چندخطیگرایی) و متغیر وابسته باید کمی باشد. همچنین، بررسی نرمال بودن دادهها و رفع ناهمسانی واریانسها توصیه میشود.