پیاده‌سازی درخت تصمیم با پایتون

درخت تصمیم یکی از الگوریتم‌های قدرتمند و محبوب است. الگوریتم درخت تصمیم پایتون در دسته‌بندی الگوریتم‌ های یادگیری ماشین نظارت‌ شده قرار دارد. این الگوریتم برای متغیرهای خروجی هم به صورت پیوسته و هم به صورت گسسته کار می‌کند. در این مقاله، ما قصد داریم یک الگوریتم درخت تصمیم در پایتون بر روی دیتابیس وزن و فاصله مرتبط با ترازوی موازنه ارائه شده در مخزن اطلاعات UCI پیاده‌سازی کنیم.

درخت تصمیم

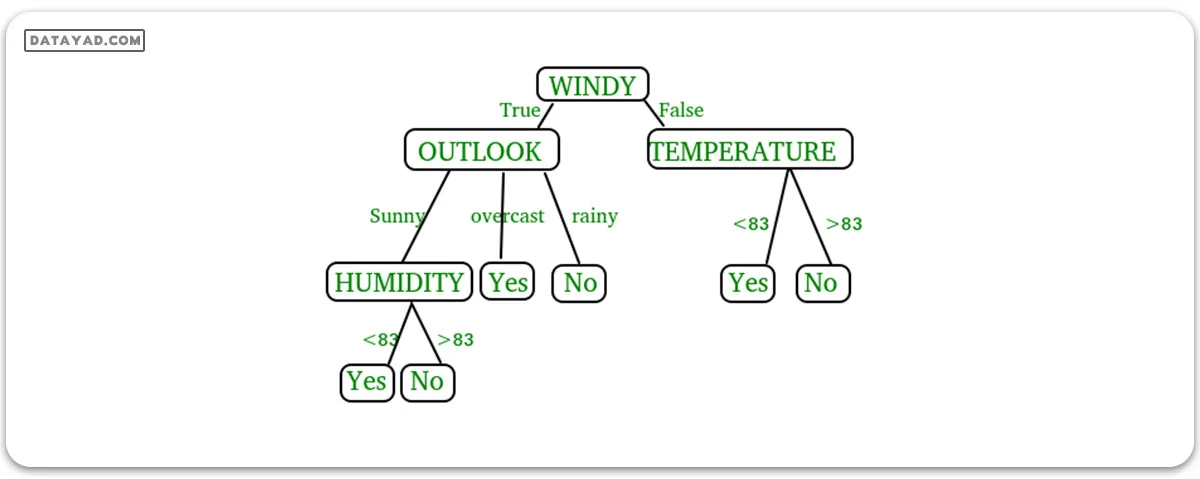
یک درخت تصمیم (Decision Tree) یک ساختار شبیه به درخت است که یک مجموعه از تصمیمات و پیامدهای ممکن آنها را نمایش می‌دهد. هر گره در درخت یک تصمیم را نمایان می‌کند و هر شاخه نتیجه آن تصمیم است. برگ‌های درخت نمایانگر تصمیمات یا پیش‌بینی‌های نهایی هستند.

درخت‌های تصمیم با روند بازگشتی تقسیم داده‌ها به زیرمجموعه‌های کوچکتر و کوچکتر ساخته می‌شوند. در هر تقسیم، داده‌ها بر اساس یک ویژگی خاص تقسیم می‌شوند و تقسیم به نحوی انجام می‌شود که اطلاعات به دست آمده (information gain) را بیشینه کند.

در شکل فوق، درخت تصمیم یک ساختار شبیه به یک نمودار جریان است که برای تصمیم‌گیری استفاده می‌شود. این درخت شامل گره اصلی (گره ریشه – WINDY)، گره‌های داخلی (OUTLOOK، TEMPERATURE) که تست‌هایی را بر روی ویژگی‌ها نمایش می‌دهند، و برگ‌ها که تصمیمات نهایی را نمایان می‌سازند، می‌باشد. شاخه‌های درخت نمایانگر نتایج ممکن تست‌ها هستند.

اجزای کلیدی درخت تصمیم در پایتون

1. گره ریشه (Root Node): گره شروع درخت تصمیم که نمایانگر مجموعه داده کلی است.
2. گره‌های شاخه (Branch Nodes): گره‌های داخلی که نقاط تصمیم را نمایش می‌دهند، جایی که داده بر اساس یک ویژگی خاص تقسیم می‌شود.
3. برگ‌ها (Leaf Nodes): دسته‌بندی نهایی یا پیش‌بینی که گره‌های پایانی را نمایان می‌سازد.
4. قوانین تصمیم (Decision Rules): قوانینی که تقسیم داده در هر گره شاخه را کنترل می‌کنند.
5. انتخاب ویژگی (Attribute Selection): فرآیند انتخاب ویژگی با بیشترین اطلاعات برای هر تقسیم را انجام می‌دهد.
6. معیار تقسیم (Splitting Criteria): معیارهایی مانند بهره اطلاعات، آنتروپی یا شاخص gini برای محاسبه تقسیم بهینه استفاده می‌شوند.

فرضیاتی که در حین استفاده از درخت تصمیم اتخاذ می‌کنیم

1. در ابتدا، تمام مجموعه آموزش را به عنوان گره ریشه در نظر می‌گیریم
2. فرض می‌شود که ویژگی‌ها برای بهره اطلاعات به صورت گسسته و برای شاخص Gini به صورت پیوسته باشند
3. بر اساس مقادیر ویژگی، رکوردها به صورت بازگشتی توزیع می‌شوند.
4. از روش‌های آماری برای ترتیب ویژگی‌ها به عنوان گره ریشه یا گره‌های داخلی استفاده می‌شود.

پیش‌زبانه درخت تصمیم

1. پیدا کردن بهترین ویژگی و قرار دادن آن به عنوان گره ریشه درخت.
2. حالا، مجموعه آموزش داده را به زیرمجموعه‌ها تقسیم کنید. هنگام ساخت هر زیرمجموعه مطمئن شوید که هر زیرمجموعه از مجموعه آموزش دارای همان مقدار برای یک ویژگی باشد.
3. با تکرار گام‌های 1 و 2 بر روی هر زیرمجموعه، گره‌های برگ را در تمام شاخه‌ها پیدا کنید.

مفهوم کلیدی در درخت تصمیم

هر دو روش شاخص Gini و بهره اطلاعات برای انتخاب از بین n ویژگی مجموعه داده استفاده می‌شوند تا تصمیم بگیرند که کدام ویژگی باید در گره ریشه یا گره داخلی قرار گیرد.

شاخص Gini:

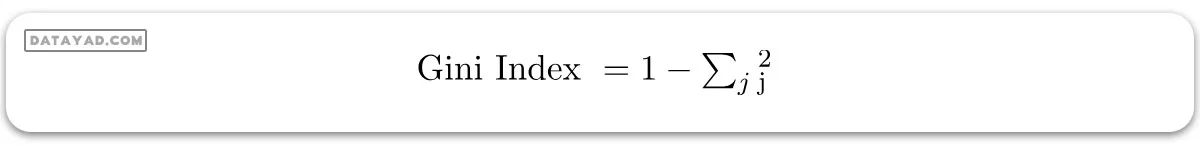
– شاخص Gini یک معیار است برای اندازه‌گیری احتمال اشتباه تشخیص یک عنصر انتخاب‌شده به صورت تصادفی.

– این به این معناست که یک ویژگی با شاخص Gini کمتر باید ترجیح داده شود.

– در Sklearn، “gini” یکی از معیارهای موجود برای شاخص Gini است و به صورت پیش‌فرض از این معیار استفاده می‌شود.

آنتروپی:

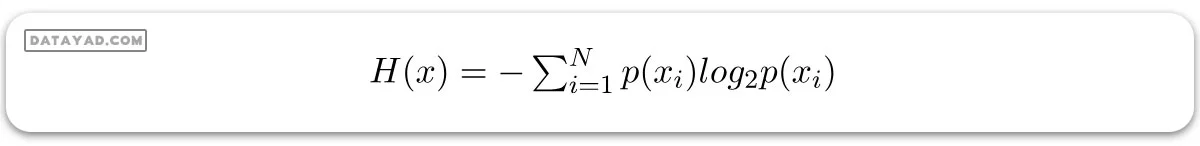
– آنتروپی اندازه‌گیری از عدم قطعیت یک متغیر تصادفی است، این ویژگی میزان خلوص یک مجموعه دلخواه از نمونه‌ها را تعیین می‌کند. هرچه آنتروپی بیشتر باشد، اطلاعات محتوا بیشتر است.

بدست آوردن بهره اطلاعات

تعریف: فرض کنید S یک مجموعه نمونه‌ها باشد، A یک ویژگی، S_v زیرمجموعه‌ای از S با A = v  و Values(A) مجموعه تمام مقادیر ممکن A باشد. در این صورت:

– آنتروپی به طور معمول زمانی که از یک گره در درخت تصمیم پایتون برای تقسیم نمونه‌های آموزش به زیرمجموعه‌های کوچکتر استفاده می‌شود تغییر می‌کند. بهره اطلاعات یک اندازه از این تغییر در آنتروپی است.

– در Sklearn، “entropy” یکی از معیارهای موجود برای بهره اطلاعات است و اگر می‌خواهیم از روش بهره اطلاعات در Sklearn استفاده کنیم، باید به صورت صریح آن را مشخص کنیم.

پیاده‌سازی درخت تصمیم در پایتون

توضیحات مجموعه داده:

Title                               : Balance Scale Weight & Distance 
Database
Number of Instances  : 625 (49 balanced, 288 left, 288 right)
Number of Attributes  : 4 (numeric) + class name = 5
Attribute Information:
1. Class Name (Target variable): 3
       L [balance scale tip to the left]
       B [balance scale be balanced]
       R [balance scale tip to the right]
2. Left-Weight: 5 (1, 2, 3, 4, 5)
3. Left-Distance: 5 (1, 2, 3, 4, 5)
4. Right-Weight: 5 (1, 2, 3, 4, 5)
5. Right-Distance: 5 (1, 2, 3, 4, 5)
Missing Attribute Values: None
Class Distribution:
      1. 46.08 percent are L
      2. 07.84 percent are B
      3. 46.08 percent are R

ترجمه فارسی توضیحات مجموعه داده بالا:

عنوان: Balance Scale Weight & Distance

مشخصات مجموعه داده:

– تعداد نمونه‌ها: 625 (49 متعادل، 288 چپ، 288 راست)

– تعداد ویژگی‌ها: 4 (عددی) + نام کلاس = 5

اطلاعات ویژگی‌ها:

1. نام کلاس (متغیر هدف): 3

   – L [تیپ مقیاس تعادل به سمت چپ]

   – B [مقیاس تعادل متعادل]

   – R [تیپ مقیاس تعادل به سمت راست

2. وزن چپ: 5 (1، 2، 3، 4، 5)
3. فاصله چپ: 5 (1، 2، 3، 4، 5)
4. وزن راست: 5 (1، 2، 3، 4، 5)
5. فاصله راست: 5 (1، 2، 3، 4، 5)

مقادیر گم‌شده ویژگی: هیچ کدام

توزیع کلاس:

1. 46.08 درصد L
2. 07.84 درصد B
3. 46.08 درصد R

شما می‌توانید جزئیات بیشتری از مجموعه داده پیدا کنید.

پیش‌نیازها:

1. sklearn:

   – در پایتون، sklearn یک بسته یادگیری ماشین است که شامل بسیاری از الگوریتم‌های یادگیری ماشین است.

   – در اینجا، ما از برخی از ماژول‌های آن مانند `train_test_split`، `DecisionTreeClassifier` و `accuracy_score` استفاده می‌کنیم.

2. NumPy:

   – این یک ماژول عددی برای پایتون است که توابع ریاضی سریعی برای محاسبات ارائه می‌کند.

   – از آن برای خواندن داده به صورت آرایه‌های numpy و برای انجام عملیات مرتبط با محاسبات استفاده می‌شود.

3. Pandas:

   – برای خواندن و نوشتن فایل‌های مختلف استفاده می‌شود.

   – با استفاده از دیتافریم‌ها، امکان انجام آسان عملیات مرتبط با داده‌ها وجود دارد.

نصب بسته‌ها

در پایتون، بسته sklearn شامل تمام بسته‌های مورد نیاز برای پیاده‌سازی الگوریتم‌های یادگیری ماشین است. شما می‌توانید بسته sklearn را با دستورات زیر نصب کنید.

استفاده از pip:

pip install -U scikit-learn

قبل از استفاده از دستور فوق، مطمئن شوید که بسته‌های scipy و numpy نصب شده باشند. اگر pip را ندارید، می‌توانید آن را با دستور زیر نصب کنید.

python get-pip.py

استفاده از conda:

conda install scikit-learn

در حین پیاده‌سازی درخت تصمیم در پایتون، به دو مرحله زیر می‌پردازیم:

1. مرحله ساخت

– پیش‌پردازش مجموعه داده.

– تقسیم مجموعه داده به قسمت آموزش و آزمون با استفاده از بسته sklearn در پایتون.

– آموزش طبقه‌بند.

2. مرحله عملیاتی

– پیش‌بینی‌ها را انجام دهید.

– دقت را محاسبه کنید.

وارد کردن داده

برای وارد کردن و دستکاری داده، از بسته pandas در پایتون استفاده می‌کنیم.

در اینجا، از یک URL استفاده می‌شود که مستقیماً مجموعه داده را از سایت UCI دریافت می‌کند و نیازی به دانلود دستی مجموعه داده ندارد. هنگامی که این کد را روی سیستم خود اجرا می‌کنید، اطمینان حاصل کنید که اتصال اینترنت فعال باشد.

از آنجا که مجموعه داده با “,” جدا شده است، باید مقدار پارامتر sep را به “,” تنظیم کنیم.

یک نکته دیگر که قابل توجه است این است که مجموعه داده هیچ هدری ندارد، بنابراین مقدار پارامتر Header را none تنظیم خواهیم کرد. اگر مقدار پارامتر header را تنظیم نکنیم، آن را به عنوان هدر اولین خط مجموعه داده در نظر می‌گیرد.

تقسیم داده

– قبل از آموزش مدل، باید مجموعه داده را به دو بخش آموزشی و آزمون تقسیم کنیم.

– برای تقسیم مجموعه داده برای آموزش و آزمون، از ماژول `train_test_split` در sklearn استفاده می‌شود.

– ابتدا باید متغیر هدف را از ویژگی‌ها در مجموعه داده جدا کنیم.

  X = balance_data.values[:, 1:5]

  Y = balance_data.values[:, 0]

– خطوط فوق از کد جدا کردن مجموعه داده هستند. متغیر X حاوی ویژگی‌ها است در حالی که متغیر Y حاوی متغیر هدف مجموعه داده است.

– مرحله بعدی، تقسیم مجموعه داده به منظور آموزش و تست است.

X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size = 0.3, random_state = 100)

– خط فوق مجموعه داده را برای آموزش و آزمون تقسیم می‌کند. زیرا ما مجموعه داده را در نسبت 70:30 بین آموزش و آزمون تقسیم می‌کنیم، مقدار test_size را به عنوان 0.3 ارسال می‌کنیم.

– متغیر random_state یک وضعیت مولد عدد تصادفی است که برای نمونه‌برداری تصادفی استفاده می‌شود.

ساخت یک درخت تصمیم در پایتون

در زیر کد برای درخت تصمیم sklearn در پایتون آورده شده است.

وارد کردن کتابخانه

وارد کردن کتابخانه‌های لازم برای پیاده‌سازی درخت تصمیم در پایتون.

# Importing the required packages
import numpy as np
import pandas as pd
from sklearn.metrics import confusion_matrix, accuracy_score, classification_report
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
import matplotlib.pyplot as plt

وارد کردن داده و بررسی

# Function to import the dataset
def importdata():
	balance_data = pd.read_csv(
		'https://archive.ics.uci.edu/ml/machine-learning-' +
		'databases/balance-scale/balance-scale.data',
		sep=',', header=None)

	# Displaying dataset information
	print("Dataset Length: ", len(balance_data))
	print("Dataset Shape: ", balance_data.shape)
	print("Dataset: ", balance_data.head())
	
	return balance_data

تقسیم داده

splitdataset(balance_data): این تابع تابع `()splitdataset` را تعریف می‌کند که مسئول تقسیم مجموعه داده به مجموعه‌های آموزشی و آزمون است. این تابع متغیر هدف (برچسب‌های کلاس) را از ویژگی‌ها جدا می‌کند و داده را با استفاده از تابع `()train_test_split` از scikit-learn تقسیم می‌کند. اندازه آزمون را به 30٪ تنظیم کرده و از یک وضعیت تصادفی به شماره 100 برای قابل تکرار بودن استفاده می‌کند.

# Function to split the dataset into features and target variables
def splitdataset(balance_data):

	# Separating the target variable
	X = balance_data.values[:, 1:5]
	Y = balance_data.values[:, 0]

	# Splitting the dataset into train and test
	X_train, X_test, y_train, y_test = train_test_split(
		X, Y, test_size=0.3, random_state=100)

	return X, Y, X_train, X_test, y_train, y_test

آموزش با استفاده از شاخص Gini

`train_using_gini(X_train, X_test, y_train)`: این تابع تابع `train_using_gini()` را تعریف می‌کند که مسئول آموزش یک طبقه‌بند درخت تصمیم با استفاده از شاخص Gini به عنوان معیار تقسیم است. این یک شیء طبقه‌بند با پارامترهای مشخص شده (معیار، وضعیت تصادفی، حداکثر عمق، حداقل نمونه برگ) ایجاد می‌کند و آن را بر روی داده آموزش آموزش می‌دهد.

def train_using_gini(X_train, X_test, y_train):

	# Creating the classifier object
	clf_gini = DecisionTreeClassifier(criterion="gini",
									random_state=100, max_depth=3, min_samples_leaf=5)

	# Performing training
	clf_gini.fit(X_train, y_train)
	return clf_gini

آموزش با استفاده از آنتروپی

`tarin_using_entropy(X_train, X_test, y_train)`: این تابع تابع `tarin_using_entropy()` را تعریف می‌کند که مسئول آموزش یک طبقه‌بند درخت تصمیم با استفاده از آنتروپی به عنوان معیار تقسیم است. این یک شیء طبقه‌بند با پارامترهای مشخص شده (معیار، وضعیت تصادفی، حداکثر عمق، حداقل نمونه برگ) ایجاد می‌کند و آن را بر روی داده آموزش آموزش می‌دهد.

def tarin_using_entropy(X_train, X_test, y_train):

	# Decision tree with entropy
	clf_entropy = DecisionTreeClassifier(
		criterion="entropy", random_state=100,
		max_depth=3, min_samples_leaf=5)

	# Performing training
	clf_entropy.fit(X_train, y_train)
	return clf_entropy

پیش‌بینی و ارزیابی

1. `prediction(X_test, clf_object)`: این تابع تابع `prediction()` را تعریف می‌کند که مسئول پیش‌بینی داده‌های تست با استفاده از شیء طبقه‌بند آموزش دیده می‌شود. این تابع داده‌های آزمون را به متد predict() طبقه‌بند منتقل می‌کند و برچسب‌های کلاس پیش‌بینی شده را چاپ می‌کند.
2. `cal_accuracy(y_test, y_pred)`: این تابع تابع `cal_accuracy()` را تعریف می‌کند که مسئول محاسبه دقت پیش‌بینی‌ها است. این تابع ماتریس درهمریختگی، امتیاز دقت و گزارش طبقه‌بندی را محاسبه و چاپ می‌کند و ارزیابی عملکرد را با جزئیات فراهم می‌کند.

# Function to make predictions
def prediction(X_test, clf_object):
	y_pred = clf_object.predict(X_test)
	print("Predicted values:")
	print(y_pred)
	return y_pred

# Placeholder function for cal_accuracy
def cal_accuracy(y_test, y_pred):
	print("Confusion Matrix: ",
		confusion_matrix(y_test, y_pred))
	print("Accuracy : ",
		accuracy_score(y_test, y_pred)*100)
	print("Report : ",
		classification_report(y_test, y_pred))

رسم درخت تصمیم

برای رسم درخت تصمیم از تابع `plot_tree` در زیرماژول `sklearn.tree` استفاده می‌شود. این تابع پارامترهای زیر را می‌پذیرد:

– `clf_object`: شیء مدل درخت تصمیم آموزش دیده.

– `filled=True`: این آرگومان نودهای درخت را بر اساس اکثریت کلاس پیش‌بینی شده با رنگ‌های مختلف پر می‌کند.

– `feature_names`: این آرگومان نام‌های ویژگی‌های استفاده شده در درخت تصمیم را فراهم می‌کند.

– `class_names`: این آرگومان نام‌های کلاس‌های مختلف را فراهم می‌کند.

– `rounded=True`: این آرگومان گوشه‌های گره‌ها را برای ظاهر زیباتر گرد می‌کند.

# Function to plot the decision tree
def plot_decision_tree(clf_object, feature_names, class_names):
	plt.figure(figsize=(15, 10))
	plot_tree(clf_object, filled=True, feature_names=feature_names, class_names=class_names, rounded=True)
	plt.show()

این کد دو طبقه‌بند درخت تصمیم تعریف می‌کند، آموزش می‌دهد و درخت‌های تصمیم را بر اساس معیارهای تقسیم مختلف (یکی با استفاده از شاخص Gini و دیگری با استفاده از آنتروپی) به تصویر می‌کشد.

if __name__ == "__main__":
	data = importdata()
	X, Y, X_train, X_test, y_train, y_test = splitdataset(data)

	clf_gini = train_using_gini(X_train, X_test, y_train)
	clf_entropy = train_using_entropy(X_train, X_test, y_train)

	# Visualizing the Decision Trees
	plot_decision_tree(clf_gini, ['X1', 'X2', 'X3', 'X4'], ['L', 'B', 'R'])
	plot_decision_tree(clf_entropy, ['X1', 'X2', 'X3', 'X4'], ['L', 'B', 'R'])

 خروجی:

DATA INFO
Dataset Length:  625
Dataset Shape:  (625, 5)
Dataset:     0  1  2  3  4
0  B  1  1  1  1
1  R  1  1  1  2
2  R  1  1  1  3
3  R  1  1  1  4
4  R  1  1  1  5

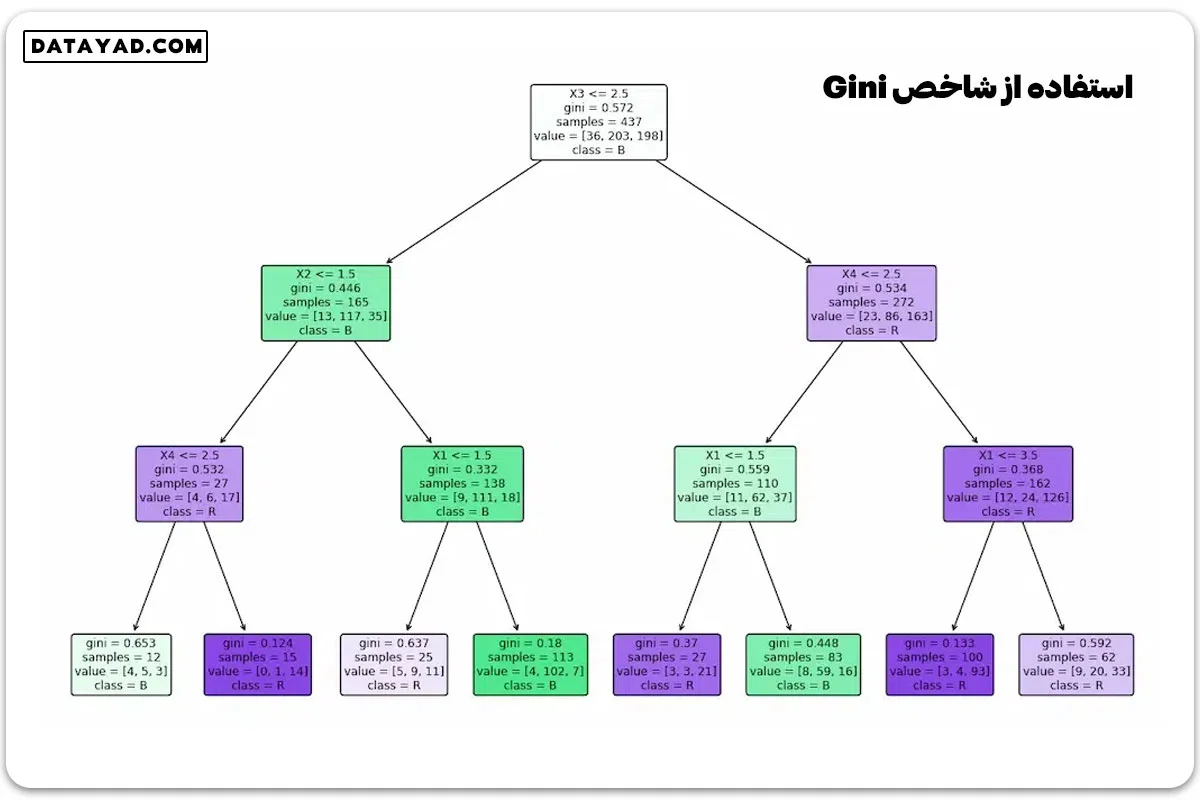
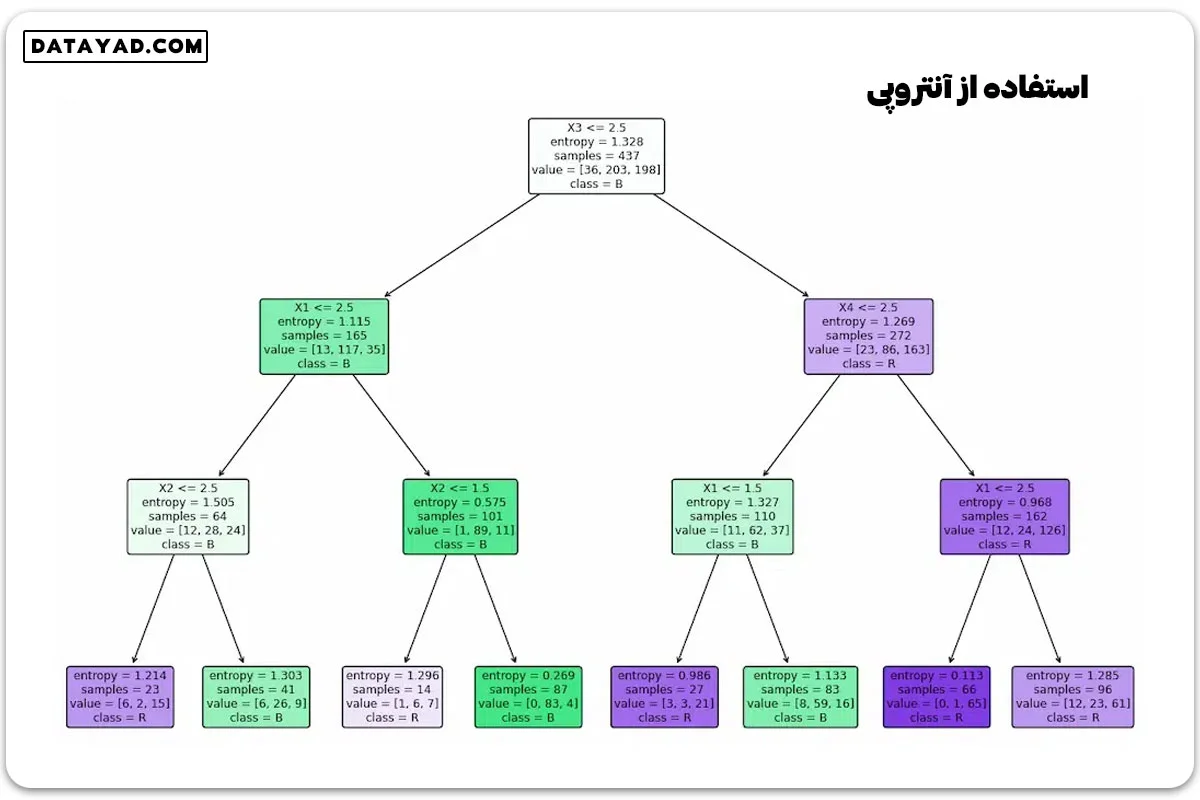
فاز عملیاتی مدل درخت تصمیم شامل موارد زیر است:

– وارد کردن و تقسیم داده برای آموزش و آزمون.

– استفاده از معیارهای Gini و آنتروپی برای آموزش دو درخت تصمیم.

– تولید برچسب‌های کلاس برای داده‌های تست با هر مدل.

– محاسبه و مقایسه دقت هر دو مدل.

ارزیابی عملکرد درخت‌های تصمیم آموزش دیده بر روی داده‌های تست ناشناخته و ارائه برداشت‌هایی از کارایی آنها برای وظیفه خاص دسته‌بندی و ارزیابی عملکرد آنها بر روی یک مجموعه داده با استفاده از ماتریس درهمریختگی، امتیاز دقت و گزارش طبقه‌بندی است.

نتایج استفاده از معیار Gini

# Operational Phase
print("Results Using Gini Index:")
y_pred_gini = prediction(X_test, clf_gini)
cal_accuracy(y_test, y_pred_gini)

 خروجی:

Results Using Gini Index:
Predicted values:
['R' 'L' 'R' 'R' 'R' 'L' 'R' 'L' 'L' 'L' 'R' 'L' 'L' 'L' 'R' 'L' 'R' 'L'
 'L' 'R' 'L' 'R' 'L' 'L' 'R' 'L' 'L' 'L' 'R' 'L' 'L' 'L' 'R' 'L' 'L' 'L'
 'L' 'R' 'L' 'L' 'R' 'L' 'R' 'L' 'R' 'R' 'L' 'L' 'R' 'L' 'R' 'R' 'L' 'R'
 'R' 'L' 'R' 'R' 'L' 'L' 'R' 'R' 'L' 'L' 'L' 'L' 'L' 'R' 'R' 'L' 'L' 'R'
 'R' 'L' 'R' 'L' 'R' 'R' 'R' 'L' 'R' 'L' 'L' 'L' 'L' 'R' 'R' 'L' 'R' 'L'
 'R' 'R' 'L' 'L' 'L' 'R' 'R' 'L' 'L' 'L' 'R' 'L' 'R' 'R' 'R' 'R' 'R' 'R'
 'R' 'L' 'R' 'L' 'R' 'R' 'L' 'R' 'R' 'R' 'R' 'R' 'L' 'R' 'L' 'L' 'L' 'L'
 'L' 'L' 'L' 'R' 'R' 'R' 'R' 'L' 'R' 'R' 'R' 'L' 'L' 'R' 'L' 'R' 'L' 'R'
 'L' 'L' 'R' 'L' 'L' 'R' 'L' 'R' 'L' 'R' 'R' 'R' 'L' 'R' 'R' 'R' 'R' 'R'
 'L' 'L' 'R' 'R' 'R' 'R' 'L' 'R' 'R' 'R' 'L' 'R' 'L' 'L' 'L' 'L' 'R' 'R'
 'L' 'R' 'R' 'L' 'L' 'R' 'R' 'R']
Confusion Matrix:  [[ 0  6  7]
 [ 0 67 18]
 [ 0 19 71]]
Accuracy :  73.40425531914893
Report :                precision    recall  f1-score   support
           B       0.00      0.00      0.00        13
           L       0.73      0.79      0.76        85
           R       0.74      0.79      0.76        90
    accuracy                           0.73       188
   macro avg       0.49      0.53      0.51       188
weighted avg       0.68      0.73      0.71       188

نتایج استفاده از آنتروپی

print("Results Using Entropy:")
y_pred_entropy = prediction(X_test, clf_entropy)
cal_accuracy(y_test, y_pred_entropy)

 خروجی:

Results Using Entropy:
Predicted values:
['R' 'L' 'R' 'L' 'R' 'L' 'R' 'L' 'R' 'R' 'R' 'R' 'L' 'L' 'R' 'L' 'R' 'L'
 'L' 'R' 'L' 'R' 'L' 'L' 'R' 'L' 'R' 'L' 'R' 'L' 'R' 'L' 'R' 'L' 'L' 'L'
 'L' 'L' 'R' 'L' 'R' 'L' 'R' 'L' 'R' 'R' 'L' 'L' 'R' 'L' 'L' 'R' 'L' 'L'
 'R' 'L' 'R' 'R' 'L' 'R' 'R' 'R' 'L' 'L' 'R' 'L' 'L' 'R' 'L' 'L' 'L' 'R'
 'R' 'L' 'R' 'L' 'R' 'R' 'R' 'L' 'R' 'L' 'L' 'L' 'L' 'R' 'R' 'L' 'R' 'L'
 'R' 'R' 'L' 'L' 'L' 'R' 'R' 'L' 'L' 'L' 'R' 'L' 'L' 'R' 'R' 'R' 'R' 'R'
 'R' 'L' 'R' 'L' 'R' 'R' 'L' 'R' 'R' 'L' 'R' 'R' 'L' 'R' 'R' 'R' 'L' 'L'
 'L' 'L' 'L' 'R' 'R' 'R' 'R' 'L' 'R' 'R' 'R' 'L' 'L' 'R' 'L' 'R' 'L' 'R'
 'L' 'R' 'R' 'L' 'L' 'R' 'L' 'R' 'R' 'R' 'R' 'R' 'L' 'R' 'R' 'R' 'R' 'R'
 'R' 'L' 'R' 'L' 'R' 'R' 'L' 'R' 'L' 'R' 'L' 'R' 'L' 'L' 'L' 'L' 'L' 'R'
 'R' 'R' 'L' 'L' 'L' 'R' 'R' 'R']
Confusion Matrix:  [[ 0  6  7]
 [ 0 63 22]
 [ 0 20 70]]
Accuracy :  70.74468085106383
Report :                precision    recall  f1-score   support

           B       0.00      0.00      0.00        13
           L       0.71      0.74      0.72        85
           R       0.71      0.78      0.74        90

    accuracy                           0.71       188
   macro avg       0.47      0.51      0.49       188
weighted avg       0.66      0.71      0.68       188

کاربردهای درخت تصمیم در پایتون

درخت‌های تصمیم در پایتون ابزارهای چند منظوره هستند و در زمینه‌های گسترده‌ای از یادگیری ماشین کاربرد دارند:

– طبقه‌بندی: پیش‌بینی نتایج دسته‌ای، مانند اینکه یک ایمیل اسپم است یا خیر.

– رگرسیون: تخمین مقادیر پیوسته؛ به عنوان مثال، پیش‌بینی قیمت خانه بر اساس ویژگی‌ها.

– انتخاب ویژگی: انتخاب ویژگی‌ها ابعاد را کاهش می‌دهد و عملکرد مدل را با تعیین اینکه کدام ویژگی‌ها بیشترین ارتباط را با یک کار خاص دارند، افزایش می‌دهد.

نتیجه‌گیری

درخت‌های تصمیم در پایتون یک روش قدرتمند و قابل فهم برای مدیریت وظایف یادگیری ماشین فراهم می‌کنند. به دلیل سهولت استفاده، کارایی و توانایی در کار با داده‌های عددی و دسته‌بندی، اینها ابزار بسیار ارزشمندی برای انواع مختلفی از کاربردها هستند. درخت‌های تصمیم، زمانی که با دقت استفاده می‌شوند، یک ابزار مفید برای انجام پیش‌بینی‌های دقیق و تحلیل‌های مفصل هستند.

سوالات متداول

1. درخت تصمیم چیست؟

   درخت‌های تصمیم نوعی الگوریتم یادگیری ماشین هستند که برای وظایف دسته‌بندی و رگرسیون مورد استفاده قرار می‌گیرند. این الگوریتم‌ها با تقسیم داده به زیرمجموعه‌های کوچکتر و کوچکتر بر اساس معیارهای خاص کار می‌کنند. تصمیم نهایی با پیروی از مسیر درختی که احتمالاً به نتیجه صحیحترین منجر می‌شود، اتخاذ می‌شود.

2. چگونه درخت‌های تصمیم عمل می‌کنند؟

   درخت‌های تصمیم با تقسیم بازگشتی داده به زیرمجموعه‌های کوچکتر عمل می‌کنند. در هر تقسیم، تصمیمی بر اساس یک معیار خاص مثل مقدار یک ویژگی خاص اتخاذ می‌شود. سپس داده بر اساس مقدار ویژگی دیگری دوباره تقسیم می‌شود و همینطور ادامه دارد. این فرآیند تا زمانی ادامه پیدا می‌کند که داده به تعدادی زیرمجموعه تقسیم شود که هر کدام نسبتاً یکنواخت باشند.

3. چگونه می‌توان درخت تصمیم را در پایتون پیاده‌سازی کرد؟

   چندین کتابخانه برای پیاده‌سازی درخت‌های تصمیم در پایتون وجود دارد. یک کتابخانه محبوب، scikit-learn است. برای پیاده‌سازی درخت تصمیم در scikit-learn، می‌توانید از کلاس DecisionTreeClassifier استفاده کنید. این کلاس دارای چندین پارامتر است که می‌توانید تنظیمات کنید، مانند معیار تقسیم داده و حداکثر عمق درخت.

4. چگونه می‌توان عملکرد یک درخت تصمیم را ارزیابی کرد؟

   چندین معیار برای ارزیابی عملکرد یک درخت تصمیم وجود دارد. یک معیار رایج accuracy است که نسبت پیش‌بینی‌های صحیح درخت را نشان می‌دهد. معیار دقت دیگر، precision، نسبت پیش‌بینی‌های مثبت صحیح به کل پیش‌بینی‌های مثبت است. معیار دیگر نیز بازخوانی است که نسبت مثبت‌های واقعی را نشان می‌دهد که توسط درخت به درستی شناسایی شده‌اند.

5. چه چالش‌هایی در استفاده از درخت‌های تصمیم وجود دارد؟

برخی از چالش‌های استفاده از درخت‌های تصمیم شامل موارد زیر هستند:

– بیش‌برازش: درخت‌های تصمیم ممکن است به بیش‌برازش مبتلا باشند، به این معنا که ممکن است داده‌های آموزش را خیلی خوب یاد بگیرند و به خوبی به داده‌های جدید تعمیم ندهند.

– تفسیرپذیری: درخت‌های تصمیم ممکن است زمانی که عمیق یا پیچیده هستند، دشوار به تفسیر باشند.

– انتخاب ویژگی: درخت‌های تصمیم ممکن است به انتخاب ویژگی‌ها حساس باشند.

– Pruning :Pruning درخت‌های تصمیم ممکن است دشوار باشد، به این معنا که حذف شاخه‌های غیرضروری از درخت ممکن است دشوار باشد.