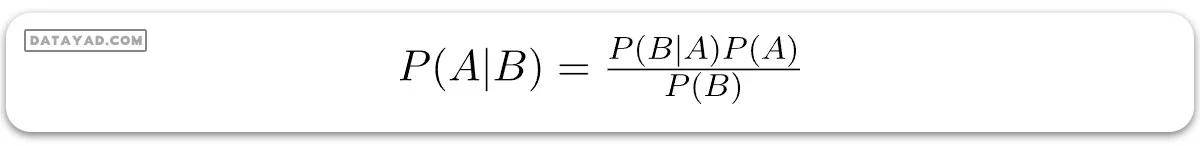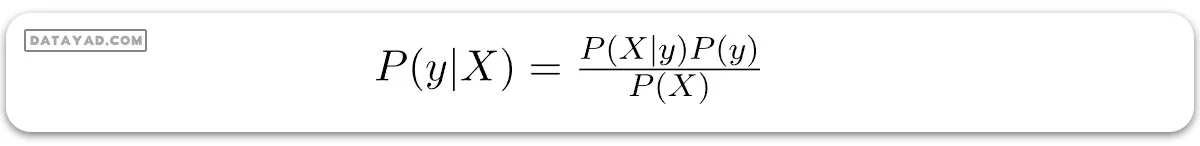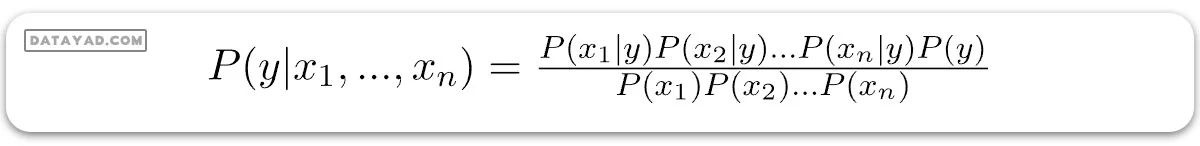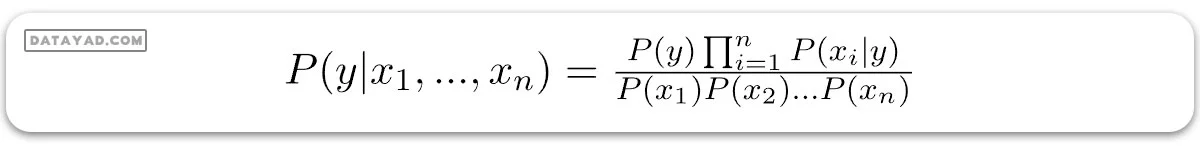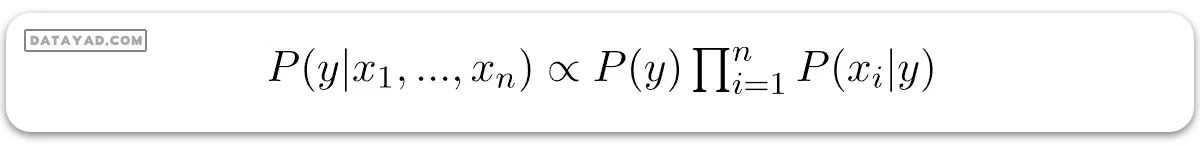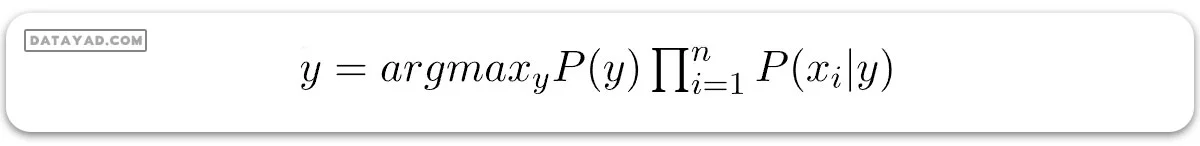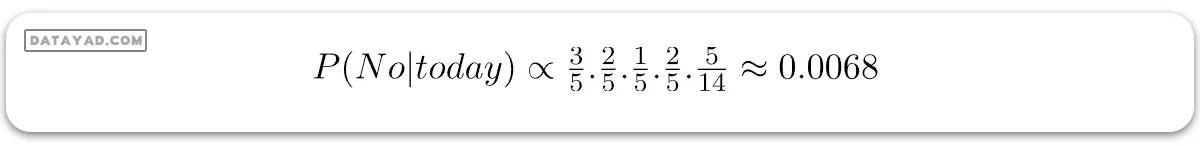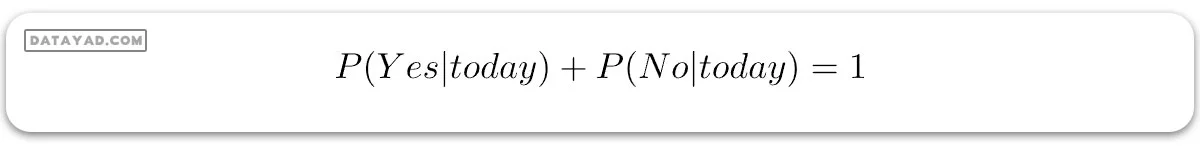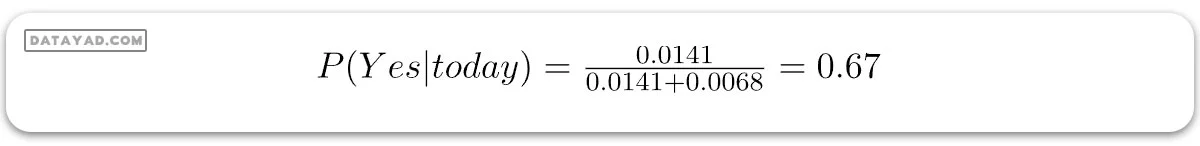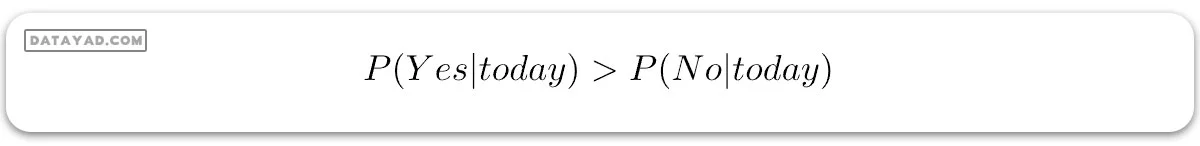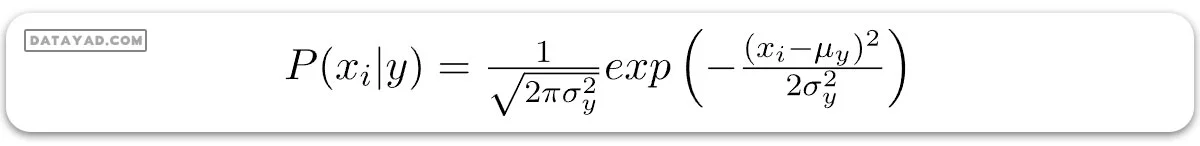دسته بندی کننده های بیز ساده (Naive Bayes)

فهرست مطالب
در درس سی و هفتم از آموزش رایگان یادگیری ماشین با پایتون به بحث در مورد نظریه پشت دستهبندیکنندههای بیز ساده (Naive Bayes Classifiers) و پیاده سازی آنها در سایت دیتایاد می پردازیم.
دسته بندی کننده های بیز ساده مجموعهای از الگوریتمهای دستهبندی هستند که بر اساس قضیه بیز کار میکنند. این الگوریتمها یک الگوریتم منفرد نیستند، بلکه خانوادهای از الگوریتمها هستند که همه آنها یک اصل مشترک دارند، یعنی هر جفت ویژگی که دستهبندی میشوند، مستقل از یکدیگر هستند.
برای شروع، بیایید یک مجموعه داده را در نظر بگیریم. یک مجموعه داده خیالی را در نظر بگیرید که شرایط آب و هوایی برای بازی گلف را توصیف میکند. با توجه به شرایط آب و هوا، هر تاپل شرایط را به عنوان مناسب («بله») یا نامناسب («نه») برای بازی گلف دستهبندی میکند.
در اینجا نمایش جدولی از مجموعه دادههای ما آمده است.
| بازی گلف | باد | رطوبت | دما | چشم انداز | |
| خیر | اشتباه | زیاد | گرم | بارانی | 0 |
| خیر | درست | زیاد | گرم | بارانی | 1 |
| بله | اشتباه | زیاد | گرم | ابری | 2 |
| بله | اشتباه | زیاد | ملایم | آفتابی | 3 |
| بله | اشتباه | معمولی | خنک | آفتابی | 4 |
| خیر | درست | معمولی | خنک | آفتابی | 5 |
| بله | درست | معمولی | خنک | ابری | 6 |
| خیر | اشتباه | زیاد | ملایم | بارانی | 7 |
| بله | اشتباه | معمولی | خنک | بارانی | 8 |
| بله | اشتباه | معمولی | ملایم | آفتابی | 9 |
| بله | درست | معمولی | ملایم | بارانی | 10 |
| بله | درست | زیاد | ملایم | ابری | 11 |
| بله | اشتباه | معمولی | گرم | ابری | 12 |
| نه | درست | زیاد | ملایم | آفتابی | 13 |
مجموعه داده به دو بخش تقسیم شده است: ماتریس ویژگی و بردار پاسخ.
✓ ماتریس ویژگی شامل تمام بردارها (سطرها) مجموعه داده است که هر بردار شامل مقادیر ویژگیهای وابسته است. در مجموعه داده بالا، ویژگیها عبارتند از ‘چشمانداز’، ‘دما’، ‘رطوبت’ و ‘باد’.
✓ بردار پاسخ شامل مقدار متغیر کلاس (پیشبینی یا خروجی) برای هر سطر از ماتریس ویژگی است. در مجموعه داده بالا، نام متغیر کلاس ‘بازی گلف’ است.
فرض:
فرض اساسی بیز ساده این است که هر ویژگی یک سهم:
✓ مستقل
✓ برابر
در نتیجه دارد.
در ارتباط با مجموعه دادههای ما، این مفهوم را میتوان به این شکل درک کرد:
✓ ما فرض میکنیم که هیچ جفتی از ویژگیها وابسته نیستند. به عنوان مثال، دمای ‘گرم’ بودن هیچ ارتباطی با رطوبت ندارد یا چشمانداز ‘بارانی’ بودن تأثیری بر باد ندارد. بنابراین، ویژگیها فرض میشوند که مستقل هستند.
✓ دوم اینکه، به هر ویژگی وزن (یا اهمیت) یکسانی داده میشود. به عنوان مثال، دانستن فقط دما و رطوبت به تنهایی نمیتواند نتیجه را به طور دقیق پیشبینی کند. هیچ یک از ویژگیها غیرمرتبط فرض نمیشوند و پیشبینی میشود که به طور یکسان به نتیجه کمک میکنند.
توجه: فرضهایی که توسط بیز ساده انجام میشوند، معمولاً در شرایط واقعی جهان درست نیستند. در واقع، فرض استقلال هیچوقت درست نیست اما اغلب در عمل خوب کار میکند.
حال، قبل از حرکت به سمت فرمول بیز ساده، فهم قضیه بیز مهم است.
قضیه بیز
قضیه بیز احتمال وقوع یک رویداد را با توجه به احتمال رویداد دیگری که قبلاً رخ داده است، مییابد. قضیه بیز به صورت ریاضی به شکل زیر بیان میشود:
که در آن A و B رویدادها هستند و P(B) ≠ 0.
– اساساً، ما در تلاش هستیم تا احتمال رویداد A را پیدا کنیم، به شرطی که رویداد B واقع شده باشد. رویداد B نیز به عنوان شاهد نامیده میشود.
– P(A) پیشینی A است (احتمال پیش از دیدن شواهد). شاهد یک مقدار ویژگی از یک نمونه ناشناخته است (در اینجا، رویداد B است).
– P(A|B) احتمال پسینی B است، یعنی احتمال رویداد بعد از دیدن شواهد.
حال، در ارتباط با مجموعه دادههای ما، میتوانیم قضیه بیز را به شکل زیر اعمال کنیم:
که در آن y متغیر کلاس و X یک بردار ویژگی وابسته (با اندازه n) است که:
برای روشن شدن، یک نمونه از بردار ویژگی و متغیر کلاس مربوطه میتواند باشد: (به سطر اول مجموعه دادهها ارجاع دهید)
X = (بارانی, گرم, زیاد, اشتباه)
y = خیر
پس به طور اساسی، P(y|X) در اینجا به معنی احتمال “عدم گلف بازی” است با توجه به اینکه شرایط آب و هوایی “چشمانداز بارانی”، “دمای گرم”، “رطوبت زیاد” و “بدونباد” باشد.
فرض Naive
حالا، وقت آن است که یک فرض naive به قضیه بیز اضافه کنیم، که استقلال بین ویژگیها است. بنابراین، اکنون ما شواهد را به اجزای مستقل تقسیم میکنیم.
حالا، اگر دو رویداد A و B مستقل باشند، پس،
P(A,B) = P(A)P(B)
بنابراین، به نتیجه زیر میرسیم:
که میتوان به شکل زیر بیان کرد:
اکنون، چون مخرج برای یک ورودی مشخص ثابت میماند، میتوانیم آن عبارت را حذف کنیم:
حال، نیاز به ایجاد یک مدل دستهبندیکننده داریم. برای این کار، احتمال مجموعه ورودیهای داده شده برای تمام مقادیر ممکن متغیر کلاس y را پیدا میکنیم و خروجی با بیشترین احتمال را انتخاب میکنیم که میتواند به صورت ریاضی به شکل زیر بیان شود:
پس، در نهایت، ما با محاسبه P(y) و P(xi | y) روبرو هستیم.
لطفاً توجه داشته باشید که P(y) همچنین به عنوان احتمال کلاس و P(xi | y) به عنوان احتمال شرطی نامیده میشود.
دسته بندیکننده های بیز ساده مختلف عمدتاً با فرضهایی که در مورد توزیع P(xi | y) در نظر میگیرند، از یکدیگر متفاوت هستند.
حالا، بیایید سعی کنیم فرمول بالا را به صورت دستی روی مجموعه دادههای آب و هوایی اعمال کنیم. برای این کار، ما نیاز به انجام برخی پیشمحاسبات روی مجموعه دادههایمان داریم.
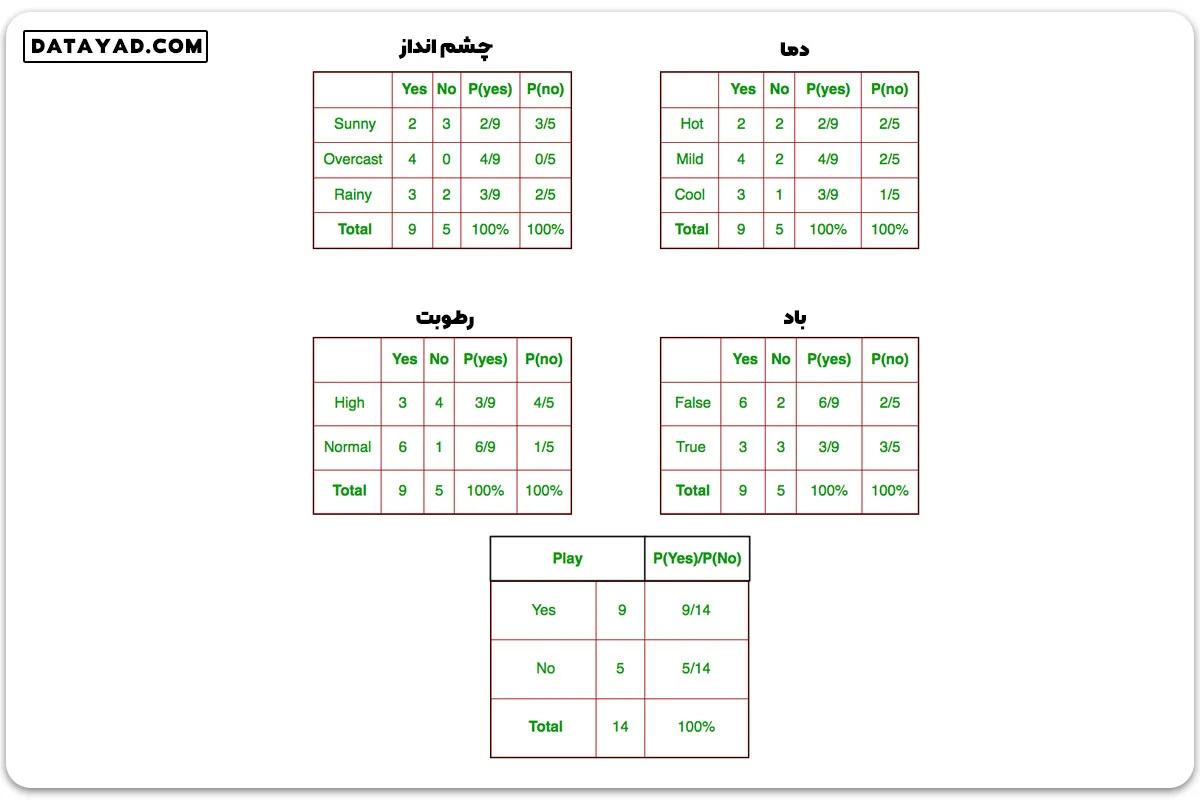
برای هر xi در X و yj در y، ما باید P(xi | yj) را بیابیم. تمام این محاسبات در جداول زیر نشان داده شده است:
پس، در شکل بالا، ما P(xi | yj) را برای هر xi در X و yj در y به صورت دستی در جداول 1 تا 4 محاسبه کردهایم. به عنوان مثال، احتمال بازی گلف با فرض اینکه دما خنک است، یعنی
P(temp. = cool | play golf = Yes) = 3/9
همچنین، ما باید احتمالات کلاس (P(y)) را بیابیم که در جدول 5 محاسبه شده است. به عنوان مثال،
P(play golf = Yes) = 9/14
حالا، پیشمحاسباتمان را تمام کردهایم و دستهبندیکننده آماده است!
بیایید آن را روی مجموعهای جدید از ویژگیها (آن را امروز مینامیم) آزمایش کنیم:
امروز = (آفتابی, گرم, معمولی, اشتباه)
پس، احتمال بازی گلف به صورت زیر داده میشود:
و احتمال عدم بازی گلف به صورت زیر داده میشود:
از آنجایی که (P(today در هر دو احتمال مشترک است، میتوانیم (P(today را نادیده بگیریم و احتمالات نسبی را به دست آوریم:
و
حال، چون:
این اعداد میتوانند با تبدیل کردن جمع آنها به 1 (نرمالسازی) به احتمال تبدیل شوند:
و
از آنجایی که:
پس، پیشبینی اینکه گلف بازی خواهد شد، ‘بله’ است.
روشی که در بالا بحث کردیم برای دادههای گسسته قابل اجرا است. در صورت دادههای پیوسته، ما نیاز به انجام برخی فرضها در مورد توزیع مقادیر هر ویژگی داریم. دسته بندی کننده های بیز ساده مختلف عمدتاً با فرضهایی که در مورد توزیع P(xi | y) انجام میدهند، متفاوت هستند.
حالا، یکی از این دستهبندیکنندهها را در اینجا بحث میکنیم.
دسته بندی کننده بیز ساده گاوسی
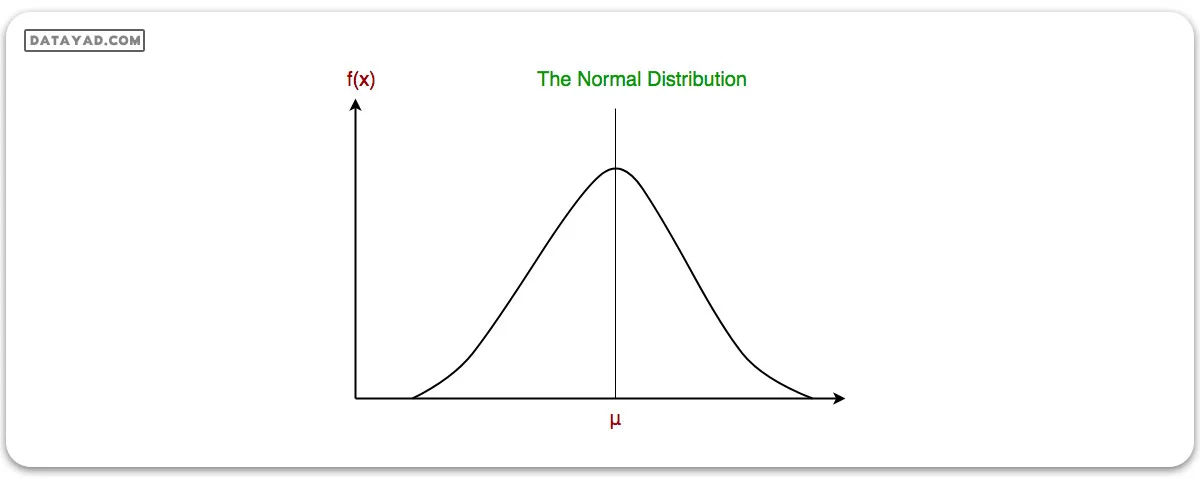
در نسخه گاوسی بیز ساده (Gaussian Naive Bayes)، فرض بر این است که مقادیر پیوسته مربوط به هر ویژگی بر مبنای توزیع گاوسی یا همان توزیع نرمال توزیع شدهاند. مانند شکل زیر، این توزیع وقتی به صورت نموداری رسم شود، شکلی مانند زنگوله دارد و دور میانگین مقادیر ویژگیها متقارن است.
بهروزرسانی جدول احتمالات پیشین برای ویژگی چشمانداز به شرح زیر است:
احتمال ویژگیها به فرض توزیع گاوسی در نظر گرفته میشود، بنابراین، احتمال شرطی به صورت زیر داده میشود:
اکنون، ما به بررسی پیادهسازی دسته بندی کننده بیز ساده گاوسی با استفاده از scikit-learn میپردازیم.
| p(no) | p(yes) | نه | بله | |
| 2.5 | 3.9 | 2 | 3 | آفتابی |
| 0.5 | 4.9 | 0 | 4 | ابری |
| 3.5 | 2.9 | 3 | 2 | بارانی |
| 100% | 100% | 5 | 9 | کامل |
# load the iris dataset
from sklearn.datasets import load_iris
iris = load_iris()
# store the feature matrix (X) and response vector (y)
X = iris.data
y = iris.target
# splitting X and y into training and testing sets
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=1)
# training the model on training set
from sklearn.naive_bayes import GaussianNB
gnb = GaussianNB()
gnb.fit(X_train, y_train)
# making predictions on the testing set
y_pred = gnb.predict(X_test)
# comparing actual response values (y_test) with predicted response values (y_pred)
from sklearn import metrics
print("Gaussian Naive Bayes model accuracy(in %):", metrics.accuracy_score(y_test, y_pred)*100)
خروجی:
Gaussian Naive Bayes model accuracy(in %): 95.0
سایر دسته بندی کننده های بیز ساده
✓ بیز ساده چندجملهای: در این مدل، بردارهای ویژگی نشاندهنده فرکانسهایی هستند که توسط توزیع چندجملهای ایجاد شدهاند. این روش عمدتاً برای دستهبندی متون و اسناد به کار میرود (در این زمینه، “فرکانس” به تعداد دفعاتی اشاره دارد که یک رویداد، مانند ظهور یک کلمه یا ویژگی خاص، در یک مجموعه داده رخ میدهد. به عنوان مثال، در دسته بندی کننده بیز ساده چندجملهای که برای دستهبندی متون استفاده میشود، فرکانس به تعداد دفعاتی اشاره دارد که یک کلمه خاص در یک سند ظاهر میشود. این رویکرد به ویژه برای تحلیل متونی که در آنها تکرار کلمات مهم است (مانند متون ادبی یا مقالات تحقیقاتی) مفید است).
✓ بیز ساده برنولی: در این مدل، ویژگیها بولینهای مستقل (متغیرهای دودویی) هستند که ورودیها را تشریح میکنند. این مدل همانند مدل چندجملهای برای دستهبندی متون محبوب است، با این تفاوت که به جای فرکانس واژگان، وجود یا عدم وجود واژگان در متن (وقوع دودویی اصطلاحات) مد نظر قرار میگیرد.
در پایان این مقاله، چند نکته مهم وجود دارد که باید به آنها توجه کرد:
✓ با وجود اینکه فرضهای دسته بندی کننده های بیز ساده بسیار سادهانگارانه به نظر میرسند، اما در بسیاری از موقعیتهای واقعی، مانند دستهبندی متون و فیلترینگ اسپم، بسیار خوب عمل کردهاند. آنها فقط به مقدار کمی داده آموزشی برای تخمین پارامترهای مورد نیاز خود نیاز دارند.
✓ دستهبندیکنندهها و یادگیرندههای بیز ساده میتوانند در مقایسه با روشهای پیچیدهتر بسیار سریعتر باشند. جداسازی توزیعهای ویژگیها بر اساس کلاس به این معنی است که هر توزیع میتواند به صورت مستقل و به عنوان یک توزیع یکبعدی تخمین زده شود. این امر در کاهش مشکلات ناشی از داشتن ابعاد بالا کمک میکند.