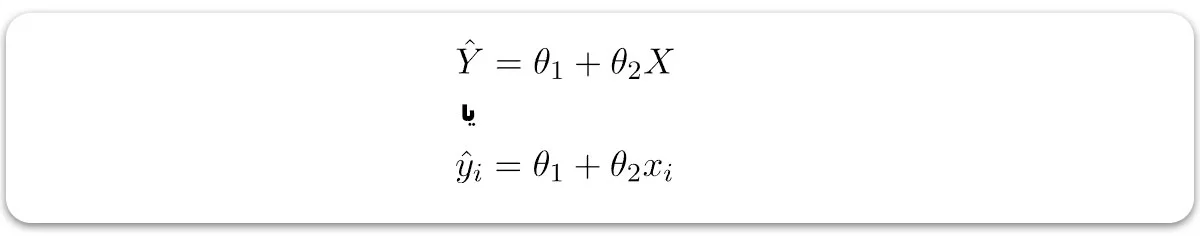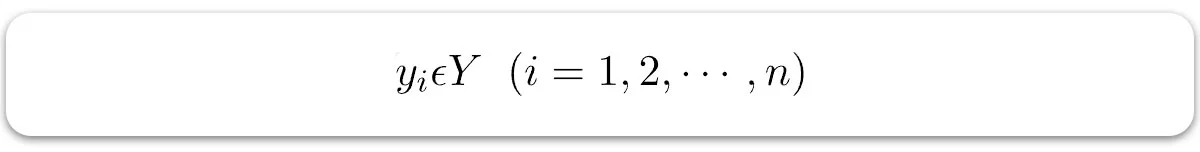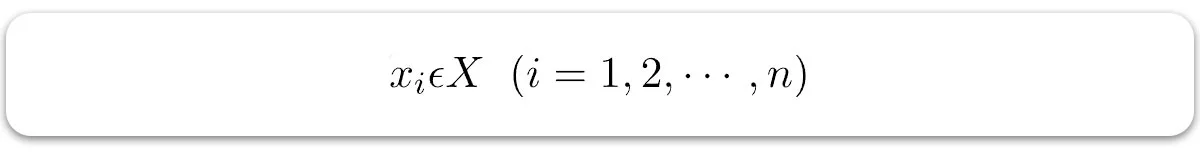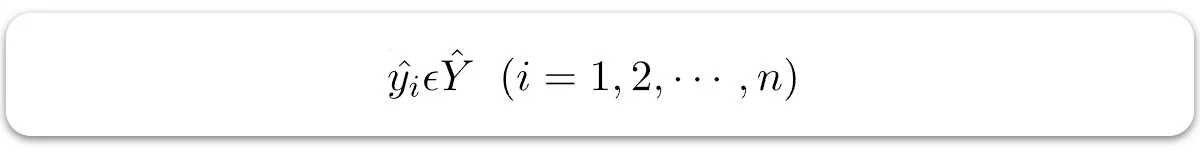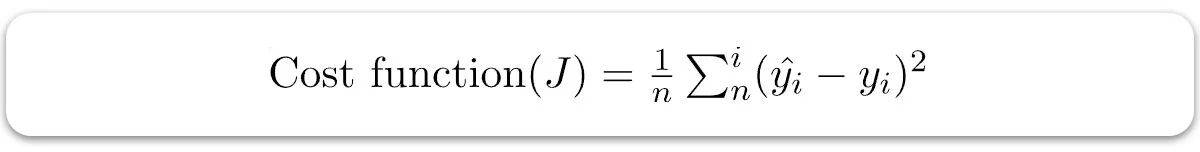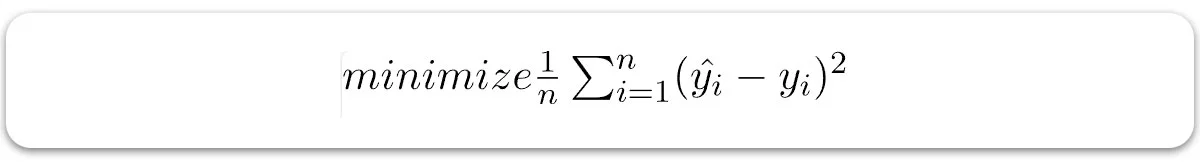یادگیری ماشین شاخهای از هوش مصنوعی است که بر روی توسعه الگوریتمها و مدلهای آماری متمرکز است که میتوانند از دادهها یاد بگیرند و پیشبینیهایی را انجام دهند.
رگرسیون خطی همچنین یک نوع الگوریتم یادگیری ماشین است. به طور خاص یک الگوریتم یادگیری ماشین نظارتشده است که از دادههای برچسبدار یاد میگیرد و نقاط داده را به تابع خطی بهینهای نگاشت میکند که میتوان از آن برای پیشبینی در مجموعه دادههای جدید استفاده کرد.
نکات مهم رگرسیون خطی و یادگیری ماشین نظارتشده
| نکات مهم | توضیحات |
| نوع الگوریتم | رگرسیون خطی یک الگوریتم یادگیری ماشین نظارتشده است که از دادههای برچسبدار برای یادگیری استفاده میکند. |
| دادههای برچسبدار | دادههایی که مقادیر هدف (خروجی) آنها از قبل مشخص شده است. |
| شاخههای یادگیری نظارتشده | – طبقهبندی: پیشبینی کلاسهای گسسته (مثلاً گربه یا سگ).
– رگرسیون: پیشبینی مقادیر پیوسته (مثلاً قیمت خانه). |
| رگرسیون خطی تکمتغیره | زمانی که تنها یک ویژگی مستقل وجود دارد. |
| رگرسیون خطی چندمتغیره | زمانی که بیش از یک ویژگی مستقل وجود داشته باشد. |
| هدف رگرسیون خطی | یافتن بهترین معادله خطی که رابطه بین متغیر وابسته و متغیرهای مستقل را نشان دهد و بتواند مقادیر متغیر وابسته را پیشبینی کند. |
| معادله خطی | معادلهای که به صورت یک خط مستقیم، رابطه بین متغیرهای وابسته و مستقل را نمایش میدهد. شیب خط نشاندهنده تغییر متغیر وابسته به ازای تغییر واحد در متغیر مستقل است. |
| کاربردها | استفاده در زمینههایی مانند مسائل مالی، اقتصاد، روانشناسی و غیره برای درک و پیشبینی رفتار یک متغیر خاص (مثلاً پیشبینی قیمت سهام یا ارزش آتی ارز). |
| وظیفه اصلی در رگرسیون | یادگیری یک تابع از دادههای X (ویژگیهای مستقل) و Y (متغیر وابسته) برای پیشبینی مقدار Y در صورت داشتن مقادیر جدید X. |
| خروجی رگرسیون خطی | مقدار Y به صورت پیوسته پیشبینی میشود. |
پس گفتیم که الگوریتم های یادگیری ماشین نظارت شده نوعی از یادگیری ماشین هستند که الگوریتم از دادههای دارای برچسب یاد میگیرد.
دادههای دارای برچسب به مجموعه دادههایی گفته میشود که مقادیر هدف آنها قبلاً مشخص شده است.

یادگیری نظارتشده دو شاخه دارد:
- طبقهبندی: در آن، کلاسِ مجموعه داده بر اساس متغیرهای ورودی مستقل پیشبینی میشود. کلاسها مقادیری دستهای یا گسسته هستند، مانند اینکه تصویر یک حیوان، گربه است یا سگ.
- رگرسیون: در این شاخه، متغیرهای خروجی پیوسته بر اساس متغیرهای ورودی مستقل پیشبینی میشوند، مانند پیشبینی قیمت خانهها بر اساس عوامل مختلفی چون مدت ساخت خانه، فاصله از جادهی اصلی، موقعیت و مساحت.

رگرسیون خطی
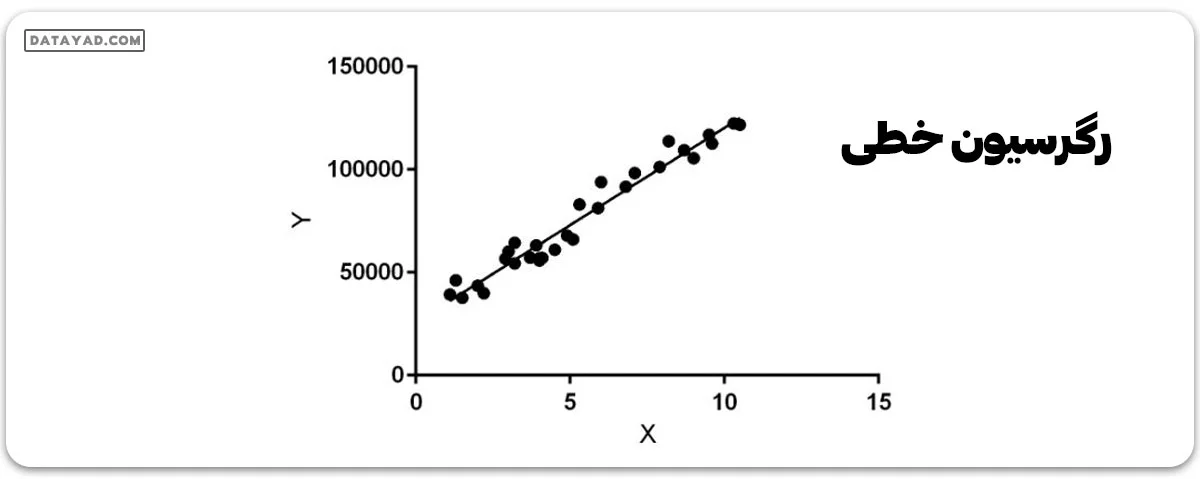
رگرسیون خطی (Supervised Learning) نوعی الگوریتم یادگیری ماشینی نظارت شده است که رابطه خطی بین متغیر وابسته و یک یا چند ویژگی مستقل را محاسبه میکند.
زمانی که تنها یک ویژگی مستقل وجود داشته باشد به آن رگرسیون خطی تکمتغیره گفته میشود و در صورتی که بیش از یک ویژگی مستقل باشد، به آن رگرسیون خطی چندمتغیره میگویند.
هدف الگوریتم خطی یافتن بهترین معادله خطی است که بتواند مقدار متغیر وابسته را بر اساس متغیرهای مستقل پیشبینی کند. این معادله، خط مستقیمی را ارائه میدهد که رابطه بین متغیرهای وابسته و مستقل را نمایش میدهد. شیب خط نشاندهنده تغییر متغیر وابسته برای تغییر واحد در متغیر(های) مستقل است.
رگرسیون خطی در بسیاری از زمینههای مختلف مانند مسائل مالی، اقتصاد و روانشناسی استفاده میشود تا رفتار یک متغیر خاص را درک و پیشبینی کند. به عنوان مثال، در مسائل مالی، رگرسیون خطی ممکن است برای درک رابطه بین قیمت سهام یک شرکت و سود آن یا برای پیشبینی ارزش آتی یک ارز بر اساس عملکرد گذشتهاش استفاده شود.
یکی از مهمترین وظایف یادگیری ماشین نظارتشده، رگرسیون است. در رگرسیون، مجموعهای از رکوردها با مقادیر X و Y وجود دارند و این مقادیر برای یادگیری یک تابع استفاده میشوند تا اگر بخواهید Y را از X ناشناختهای پیشبینی کنید، بتوانید از این تابع یادگرفته شده استفاده کنید. در رگرسیون، باید مقدار Y را پیدا کنیم، بنابراین به یک تابع نیاز داریم که در صورت رگرسیون، Y پیوستهای را با توجه به X به عنوان ویژگیهای مستقل پیشبینی کند.
در اینجا Y به عنوان متغیر وابسته یا متغیر هدف شناخته میشود و X به عنوان متغیر مستقل نامیده میشود که همچنین به عنوان پیشبینیکننده Y شناخته میشود. انواع مختلفی از توابع یا مدلها وجود دارند که میتوانند برای رگرسیون استفاده شوند. تابع خطی سادهترین نوع تابع است. در اینجا، X ممکن است یک ویژگی تکی یا چندین ویژگی باشد که مسئله را معرفی میکنند.

هدف الگوریتم رگرسیون خطی در یادگیری ماشین چیست ؟
الگوریتمهای رگرسیون خطی در یادگیری ماشین به دنبال یافتن بهترین خط برازش برای دادهها هستند تا بتوانند ارتباط میان متغیرهای مستقل و وابسته را بهطور دقیقتری مدلسازی کنند. یکی از اصلیترین اهداف این الگوریتمها، به حداقل رساندن خطاها است که به معنای کاهش تفاوت بین مقادیر واقعی و مقادیر پیشبینیشده میباشد. در این راستا روش حداقل مربعات بهعنوان یک تکنیک کلیدی استفاده میشود که با محاسبه مجموع مربعات خطاها، ضرایب بهینه را برای معادله رگرسیون تعیین میکند. این روش به ما کمک میکند تا بهترین برازش ممکن را برای دادهها پیدا کنیم و در نتیجه پیشبینیهای دقیقتری انجام دهیم.
علاوه بر این، ضریب تعیین (R²) نیز یکی از معیارهای مهم در ارزیابی کیفیت مدل رگرسیون است. این ضریب نشاندهنده نسبت واریانس متغیر وابستهای است که توسط متغیرهای مستقل توضیح داده میشود. به عبارت دیگر ضریب تعیین نشان میدهد که چه مقدار از تغییرات در متغیر وابسته با استفاده از مدل رگرسیون قابل توجیه است. با استفاده از این معیار، میتوانیم عملکرد مدل را ارزیابی کنیم و بفهمیم که آیا مدل ما توانسته است ارتباط مناسبی بین متغیرها برقرار کند یا خیر؟
در کنار رگرسیون خطی، الگوریتم رگرسیون لجستیک نیز یکی از روشهای مهم در یادگیری ماشین به شمار میرود، بهویژه زمانی که متغیر وابسته از نوع طبقهبندیشده (دستهای) باشد. رگرسیون لجستیک به جای پیشبینی مقدار عددی، احتمال تعلق یک نمونه به یک کلاس خاص را پیشبینی میکند و در بسیاری از مسائل دستهبندی مانند تشخیص بیماری، فیلتر اسپم و تحلیل ریسک کاربرد دارد.
برای درک بهتر این مفاهیم میتوانید از آموزش رایگان شبکه عصبی ما نیز بهره ببرید.
به نقل از وب سایت geeksforgeeks.org:
“رگرسیون خطی یک الگوریتم یادگیری ماشین نظارتشده است که با استفاده از دادههای برچسبگذاریشده، رابطه خطی بین متغیر وابسته و یک یا چند متغیر مستقل را از طریق برازش یک معادله خطی محاسبه میکند. این الگوریتم برای پیشبینی خروجیهای پیوسته مانند قیمت خانه بر اساس عواملی نظیر سن خانه، موقعیت، مساحت و تعداد اتاقها کاربرد دارد. از مزایای کلیدی رگرسیون خطی میتوان به سادگی، شفافیت و قابلیت تفسیر آن اشاره کرد، چراکه ضریبهای مدل بهوضوح تأثیر هر متغیر مستقل را نشان میدهند و درک روابط بین دادهها را تسهیل میکنند. این ویژگیها باعث میشود رگرسیون خطی پایهای برای درک و توسعه الگوریتمهای پیشرفتهتر باشد.”
رگرسیون خطی وظیفه پیشبینی مقدار یک متغیر وابسته (y) بر اساس یک متغیر مستقل داده شده (x) را انجام میدهد. از این رو، به آن رگرسیون خطی گفته میشود. در شکل بالا، X (ورودی) تجربه کاری و Y (خروجی) حقوق فرد است. خط رگرسیون، خط بهترین fit برای مدل ما است.
فرضیات مدل رگرسیون خطی
برای اینکه مدل رگرسیون خطی به درستی کار کند و نتایج قابل اتکایی ارائه دهد، باید چند فرض اساسی را برآورده کند:
✓ خطی بودن
بین متغیرهای مستقل و وابسته باید یک ارتباط خطی وجود داشته باشد، یعنی هر تغییری در متغیر مستقل باید باعث یک تغییر متناسب و خطی در متغیر وابسته شود.
✓ استقلال
هر مشاهدهای در مجموعه دادهها باید مستقل از مشاهدات دیگر باشد، به این معنی که مقدار متغیر وابسته یک نمونه نباید تحت تاثیر مقدار متغیر وابسته نمونهای دیگر باشد.
✓ واریانس همسان
واریانس خطاها در تمام سطوح متغیر(های) مستقل باید یکسان باشد، به این معنی که میزان متغیر مستقل نباید تاثیری بر میزان پراکندگی خطاها داشته باشد.
✓ نرمالیتی
خطاها در مدل باید به صورت توزیع نرمال باشند.
✓ عدم وجود همخطی چندگانه
نباید بین متغیرهای مستقل ارتباط قوی وجود داشته باشد، یعنی متغیرهای مستقل نباید به شدت به یکدیگر وابسته باشند.
تابع فرض برای رگرسیون خطی
با توجه به اینکه قبلاً فرض کردهایم ویژگی مستقل ما تجربه کاری یعنی ( X) است و حقوق متناظر ( Y) به عنوان متغیر وابسته میباشد، بیایید فرض کنیم یک رابطه خطی بین ( X) و ( Y) وجود دارد، پس میتوان حقوق را با استفاده از رابطه زیر پیشبینی کرد:
در اینجا:
– برچسبها به دادهها داده میشوند (یادگیری نظارتشده).
– ورودیها دادههای مستقل آموزشی هستند (تکمتغیره – یک متغیر ورودی (پارامتر)).
– مقادیر پیشبینی شده هستند.
مدل با پیدا کردن بهترین مقادیر برای θ1 و θ2 بهترین خط برازش رگرسیونی را به دست میآورد.
- θ1: مقدار برش با محور عمودی (عرض از مبدأ)
- θ2: ضریب ( X ) (شیب خط)
پس از یافتن بهترین مقادیر برای θ1 و θ2، ما به خطی دست پیدا میکنیم که دادهها را به بهترین شکل ممکن تطابق میدهد. بنابراین، هنگامی که مدلمان را برای پیشبینی به کار میبریم، این مدل مقدار y را برای مقدار ورودی x پیشبینی خواهد کرد.
تابع هزینه
تابع هزینه یا تابع ضرر، چیزی جز خطا یا تفاوت بین مقدار پیشبینی شده و مقدار واقعی ( Y) نیست. این مقدار، خطای میانگین مربعات (MSE) بین مقدار پیشبینی شده و مقدار واقعی است. تابع هزینه (J) میتواند به صورت زیر نوشته شود:
برای رسیدن به بهترین خط تطابق، چگونه θ1 و θ2 را بروز کنیم؟
برای به دست آوردن خط تطابق بهتر، مدل ما سعی میکند مقادیر هدف را به نحوی پیشبینی کند که تفاوت خطا میان مقادیر پیشبینی شده و مقادیر واقعی (Y) کمینه شود. پس، بروزرسانی مقادیر θ1 و θ2 برای رسیدن به کمترین میزان خطا بین مقدار پیشبینی شده (pred) و مقدار واقعی (y) اهمیت زیادی دارد.
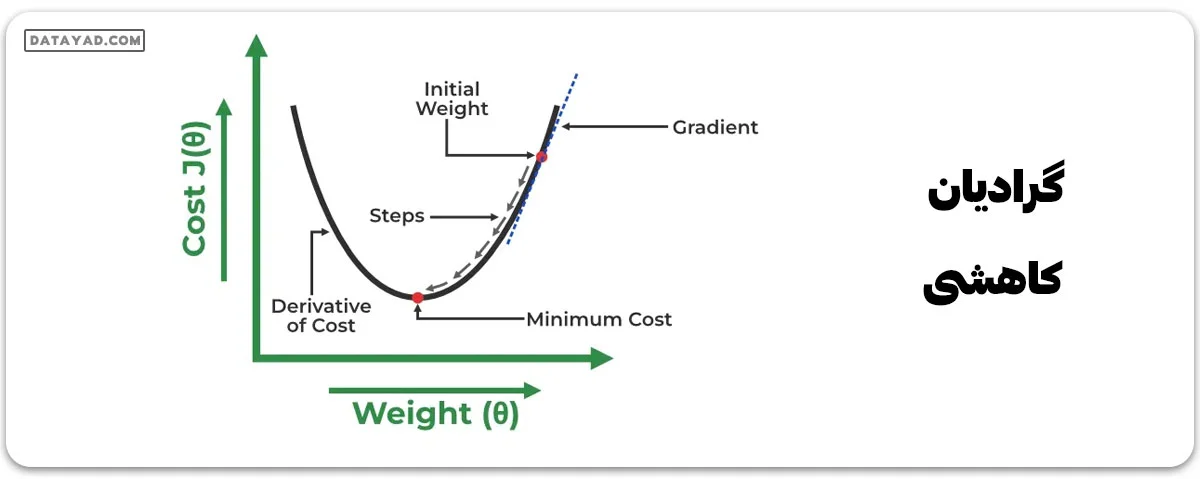
گرادیان کاهشی
رگرسیون خطی میتواند با استفاده از الگوریتم بهینهسازی گرادیان کاهشی (Gradient Descent) آموزش داده شود، آن هم با تغییر مکرر پارامترهای مدل برای کاهش خطای میانگین مربعات (MSE) مدل در یک مجموعه داده آموزشی.
برای بهروزرسانی مقادیر θ1 و θ2 به منظور کاهش تابع هزینه (کمینه کردن مقدار RMSE) و دستیابی به خط تطابق بهتر، مدل از گرادیان کاهشی استفاده میکند. ایده این است که با مقادیر تصادفی θ1 و θ2 شروع کنیم و سپس به صورت تکراری مقادیر را بهروزرسانی کنیم تا به کمترین هزینه برسیم.
گرادیان چیزی جز مشتق نیست که تأثیرات جزئی تغییرات در ورودیها را بر خروجیهای تابع تعریف میکند.
بیایید تابع هزینه (J) را نسبت به θ1 و θ2 مشتق بگیریم:
هدف از رگرسیون خطی پیدا کردن ضرایبی برای یک معادله خطی است که دادههای آموزشی را به بهترین شکل توصیف کند. میتوان ضرایب را با حرکت در خلاف جهت شیب خطای میانگین مربعات نسبت به این ضرایب تغییر داد. برای این کار، عرض از مبدأ و ضریب مربوط به (X) را میتوان با استفاده از نرخ یادگیری به روز رسانی کرد.
منظم سازی یا Regularization چیست؟
الگوریتمهای رگرسیون خطی در یادگیری ماشین با استفاده از روشهای منظمسازی (Regularization) به دنبال بهینهسازی مدلها و کاهش خطاها هستند. این روشها معمولاً با استفاده از «حداقل مربعات عادی» (Ordinary Least Squares) عمل میکنند که هدف آن به حداقل رساندن مجموع مربعات باقیمانده است. در این فرآیند فاصله هر نقطه داده تا خط رگرسیون محاسبه شده و سپس مربع این فاصلهها جمعآوری میشود. این تکنیک به ما کمک میکند تا ضرایب بهینه را برای مدل رگرسیونی تعیین کنیم و از بروز مشکلاتی مانند بیشبرازش جلوگیری کنیم.
همچنین روشهای منظمسازی موجب کاهش پیچیدگی مدل میشوند. این کار با استفاده از اندازه مطلق یا تعداد ضرایب در مدل انجام میشود. این فرآیند در یادگیری عمیق با پایتون اهمیت زیادی دارد، زیرا میتواند به انتخاب ویژگیهای مهمتر و حذف متغیرهای کماهمیت کمک کند. در کل هدف نهایی از این روشها ایجاد مدلی است که هم دقت بالایی داشته و هم از پیچیدگی غیرضروری جلوگیری کند تا بتواند عملکرد خوبی در دادههای جدید داشته باشد. برای درک بهتر میتوانید از دوره آموزش رایگان پایتون ما کمک بگیرید.
ساخت مدل رگرسیون خطی از صفر
وارد کردن کتابخانههای ضروری:
import pandas as pd import numpy as np import matplotlib.pyplot as plt import matplotlib.axes as ax
بارگذاری مجموعه دادهها و جداسازی متغیرهای ورودی و هدف
data = pd.read_csv(‘data_for_lr.csv’)
# Drop the missing values data = data.dropna() # training dataset and labels train_input = np.array(data.x[0:500]).reshape(500,1) train_output = np.array(data.y[0:500]).reshape(500,1) # valid dataset and labels test_input = np.array(data.x[500:700]).reshape(199,1) test_output = np.array(data.y[500:700]).reshape(199,1)
مراحل ساخت مدل رگرسیون خطی
- در انتشار رو به جلو، تابع رگرسیون خطی ( Y=mx+c) با اختصاص اولیه مقدار تصادفی به پارامترها (m و c) اعمال میشود.
- سپس تابعی برای یافتن تابع هزینه نوشتهایم، یعنی میانگین …
class LinearRegression:
def __init__(self):
self.parameters = {}
def forward_propagation(self, train_input):
m = self.parameters['m']
c = self.parameters['c']
predictions = np.multiply(m, train_input) + c
return predictions
def cost_function(self, predictions, train_output):
cost = np.mean((train_output - predictions) ** 2)
return cost
def backward_propagation(self, train_input, train_output, predictions):
derivatives = {}
df = (train_output - predictions) * -1
dm = np.mean(np.multiply(train_input, df))
dc = np.mean(df)
derivatives['dm'] = dm
derivatives['dc'] = dc
return derivatives
def update_parameters(self, derivatives, learning_rate):
self.parameters['m'] = self.parameters['m'] - learning_rate * derivatives['dm']
self.parameters['c'] = self.parameters['c'] - learning_rate * derivatives['dc']
def train(self, train_input, train_output, learning_rate, iters):
#initialize random parameters
self.parameters['m'] = np.random.uniform(0,1) * -1
self.parameters['c'] = np.random.uniform(0,1) * -1
#initialize loss
self.loss = []
#iterate
for i in range(iters):
#forward propagation
predictions = self.forward_propagation(train_input)
#cost function
cost = self.cost_function(predictions, train_output)
#append loss and print
self.loss.append(cost)
print("Iteration = {}, Loss = {}".format(i+1, cost))
#back propagation
derivatives = self.backward_propagation(train_input, train_output, predictions)
#update parameters
self.update_parameters(derivatives, learning_rate)
return self.parameters, self.loss
آموزش مدل
#Example usage linear_reg = LinearRegression() parameters, loss = linear_reg.train(train_input, train_output, 0.0001, 20)
Iteration = 1, Loss = 5363.981028641572 Iteration = 2, Loss = 2437.9165904342512 Iteration = 3, Loss = 1110.3579137897523 Iteration = 4, Loss = 508.043071737168 Iteration = 5, Loss = 234.7721607488976 Iteration = 6, Loss = 110.78884574712548 Iteration = 7, Loss = 54.53747840152165 Iteration = 8, Loss = 29.016170730218153 Iteration = 9, Loss = 17.43712517102535 Iteration = 10, Loss = 12.183699375121314 Iteration = 11, Loss = 9.800214272338595 Iteration = 12, Loss = 8.718824440889573 Iteration = 13, Loss = 8.228196676299069 Iteration = 14, Loss = 8.005598315794709 Iteration = 15, Loss = 7.904605192804647 Iteration = 16, Loss = 7.858784500769819 Iteration = 17, Loss = 7.837995601770647 Iteration = 18, Loss = 7.828563654998014 Iteration = 19, Loss = 7.824284370030002 Iteration = 20, Loss = 7.822342853430061
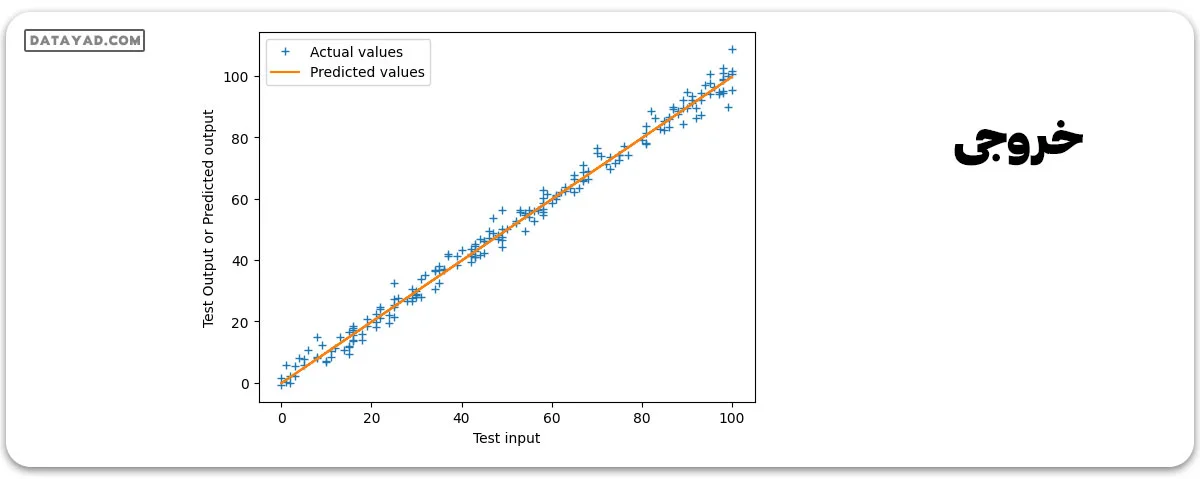
پیشبینی نهایی و رسم خط رگرسیون
#Prediction on test data
y_pred = test_input*parameters['m'] + parameters['c']
# Plot the regression line with actual data pointa
plt.plot(test_input, test_output, '+', label='Actual values')
plt.plot(test_input, y_pred, label='Predicted values')
plt.xlabel('Test input')
plt.ylabel('Test Output or Predicted output')
plt.legend()
plt.show()
کدهای رگرسیون خطی در یادگیری ماشین
برای پیادهسازی الگوریتم رگرسیون خطی در یادگیری ماشین دو روش اصلی وجود دارد. روش اول استفاده از کتابخانه «Scikit Learn» در زبان برنامهنویسی پایتون است. با وارد کردن مدل رگرسیون خطی از این کتابخانه، میتوان به سادگی و به طور مستقیم از امکانات آن بهره برد و مدل را بر روی دادههای آموزشی اجرا کرد. این کتابخانه ابزارهای متنوعی برای تجزیه و تحلیل دادهها و پیشبینی نتایج ارائه میدهد که به کاربران کمک میکند تا به راحتی مدلهای رگرسیونی را پیادهسازی کنند. روش دوم شامل نوشتن الگوریتم رگرسیون خطی به صورت دستی با استفاده از معادلات ریاضی است. این روش به کاربران این امکان را میدهد که کنترل بیشتری بر روی فرآیند یادگیری داشته باشند و درک عمیقتری از نحوه عملکرد الگوریتم پیدا کنند.
برای مثال میتوان با محاسبه مجموع مربعات خطاها و بهکارگیری روش حداقل مربعات عادی، ضرایب مدل را تعیین کرد. در این زمینه، مهمترین کاربرد های پایتون شامل تجزیه و تحلیل دادهها، مدلسازی و پیشبینی نتایج است که به کاربران این امکان را میدهد تا با استفاده از دادههای واقعی، نتایج دقیقی بدست آورند. برای درک بهتر میتوانید به آموزش رایگان یادگیری ماشین با پایتون مراجعه کنید.
به نقل از وب سایت geeksforgeeks.org:
“رگرسیون خطی یکی از انواع الگوریتمهای یادگیری ماشین نظارتشده است که از مجموعه دادههای برچسبگذاریشده یاد میگیرد و نقاط داده را با توابع خطی بهینهسازیشده مطابقت میدهد که میتوان از آنها برای پیشبینی در مجموعه دادههای جدید استفاده کرد. این الگوریتم رابطه خطی بین متغیر وابسته و یک یا چند ویژگی مستقل را با برازش یک معادله خطی بر اساس دادههای مشاهدهشده محاسبه میکند. رگرسیون خطی متغیرهای خروجی پیوسته را بر اساس متغیرهای ورودی مستقل پیشبینی میکند. به عنوان مثال، اگر بخواهیم قیمت یک خانه را پیشبینی کنیم، عواملی مانند سن خانه، فاصله از جاده اصلی، موقعیت مکانی، مساحت و تعداد اتاقها را در نظر میگیریم. رگرسیون خطی با در نظر گرفتن رابطه خطی بین این ویژگیها و قیمت خانه، از تمام این پارامترها برای پیشبینی قیمت استفاده میکند.”
سوالات متداول
رگرسیون خطی در یادگیری ماشین چه کاربردهایی دارد؟
رگرسیون خطی، یک تکنیک آماری پرطرفدار و آسان در یادگیری ماشین است که برای تحلیل و پیشبینی به کار میرود. این الکوریتم برای بررسی ارتباط بین دادههای عددی و پیوسته مانند فروش، درآمد، سن و قیمتگذاری مناسب است. هدف اصلی آن، ایجاد یک مدل برای تعیین نحوه تاثیر یک یا چند متغیر مستقل بر یک متغیر وابسته است. با این مدل میتوان مقادیر متغیر وابسته را بر پایه دگرگونیهای متغیرهای مستقل پیشبینی کرد.
چه فرضیاتی در مدل رگرسیون خطی باید رعایت شود؟
رگرسیون خطی بر پایه فرضیاتی استوار است که دقت و اعتبار مدل را تضمین میکنند. یکی از این فرضیات، صفر بودن میانگین خطاها است که نشان میدهد مدل به طور سیستماتیک مقادیر را بیش یا کمتر از واقعیت پیشبینی نمیکند. همچنین واریانس ثابت خطاها بیانگر یکنواختی پراکندگی خطاها در طول محدوده مقادیر پیشبینیشده است. عدم همبستگی بین خطاها، بیانگر مستقل بودن خطاها از یکدیگر و در نهایت نرمال بودن توزیع متغیر وابسته میباشد. علاوه بر این عدم وجود همخطی بین متغیرهای مستقل، از ایجاد مشکلات در تخمین ضرایب مدل جلوگیری میکند.
چگونه میتوان دقت مدل رگرسیون خطی را ارزیابی کرد؟
برای ارزیابی دقت مدل رگرسیون خطی، چندین معیار متداول وجود دارد. ضریب تعیین (R²) یکی از رایجترین روشهاست که نشاندهنده نسبت تغییرات توضیحدادهشده توسط مدل است و هر چه به یک نزدیکتر باشد، دقت مدل بالاتر است. میانگین مربع خطا (MSE) نیز معیاری برای اندازهگیری میانگین اختلاف مربع مقادیر واقعی و پیشبینی شده است که به ما کمک میکند تا میزان خطا را در پیشبینیها بررسی کنیم. همچنین ریشه میانگین مربعات خطا (RMSE) که به صورت ریشهگیری از MSE محاسبه میشود، میتواند برای شناسایی خطاهای بزرگتر مورد استفاده قرار گیرد. این معیارها به تحلیلگران کمک میکنند تا کیفیت و کارایی مدلهای رگرسیون را به طور دقیق ارزیابی کنند.
چه تفاوتی بین رگرسیون خطی ساده و رگرسیون خطی چندمتغیره وجود دارد؟
رگرسیون خطی بر اساس تعداد متغیرهای مستقل و وابسته، دستهبندی میشود. در صورتی که تنها یک متغیر مستقل در مدل وجود داشته باشد، آن را رگرسیون خطی ساده مینامند که سادهترین شکل این الگوریتم است. اما اگر تعداد متغیرهای مستقل بیشتر از یک باشد، با یک مدل رگرسیون خطی چندگانه روبرو هستیم که پیچیدگی بیشتری دارد. از سوی دیگر اگر هدف پیشبینی چندین متغیر وابسته به جای یک متغیر باشد، از مدل رگرسیون خطی چندمتغیره استفاده میشود.