پیش‌ پردازش داده‌ ها در پایتون

در درس دهم از آموزش رایگان یادگیری ماشین با پایتون در سایت دیتایاد می خواهیم در مورد پیش پردازش داده ها در پایتون صحبت کنیم.

اصول و قواعد در پیش پردازش داده ها

آیا می دانید پیش پردازش داده ها در یادگیری ماشین چه اهمیتی دارد؟ پیش‌پردازش داده‌ها یکی از مهم‌ترین مراحل در یادگیری ماشینی و علم داده است که مراحل مختلفی دارد. این مراحل شامل بهبود کیفیت داده‌ها و آماده‌سازی آن‌ها برای مدل‌سازی می‌باشد. یکی از این مراحل پاکسازی داده نام دارد. در این مرحله داده‌های گمشده، نادرست یا نویزی شناسایی و تصحیح می‌شوند. این فرآیند باعث کاهش افت کیفیت مجموعه‌داده شده و فقط داده‌های باکیفیت به مراحل بعدی می‌روند. یکی از مراحل کلیدی در این پروسه، شناسایی و حذف ناهنجاری‌ها است. مرحله بعدی طبقه‌بندی داده نام دارد که جزو کلیدی‌ترین مراحل در این فرآیند می‌باشد. این فرآیند موجب جلوگیری از بروز مشکلات در مراحل بعدی شده و اطمینان می‌دهد که داده‌ها به شکل مناسبی برای مدل‌سازی آماده شوند.

علم داده، با استفاده از تحلیل‌های آماری، یادگیری ماشین و برنامه‌نویسی، به کشف دانش و بینش از داده‌ها می‌پردازد. این فرایند شامل تصفیه و تبدیل اطلاعات نامنظم به داده‌های قابل تحلیل است.

دانشمندان داده با استفاده از ابزار و تکنیک‌های متنوع، الگوهای مخفی در داده‌ها را کشف می‌کنند تا به تصمیم‌گیری و فرصت‌های جدید کمک کنند. این علم در زمینه‌هایی چون کسب و کار، مهندسی و علوم انسانی کاربرد دارد.

مرحله مهم بعدی کاهش بعد داده است که به تسریع و کارآمدتر کردن مدل‌های یادگیری ماشین کمک شایانی می‌کند. مرحله پایانی یکپارچه‌سازی مجموعه‌داده برای ایجاد یک پایگاه داده منسجم و قابل استفاده است. این مرحله یک پیش‌نیاز ضروری برای اجرای موثر الگوریتم‌های یادگیری ماشین می‎‌باشد. توجه داشته باشید که برای درک بهتر این مفاهیم شما باید ابتدا بدانید ماشین لرنینگ چیست؟

پیش‌ پردازش داده

در پیش پردازش داده ها در یادگیری ماشین داده‌های خام و غیرساختاریافته به داده‌هایی با شکلی تمیز، سازمان‌یافته و قابل تحلیل در می‌آیند. این مرحله جزو مراحل مهم در یادگیری ماشین می‌باشد و کار آن شناسایی و اصلاح داده‌های ناقص، تبدیل داده‌های متنی به عددی، حذف مقادیر نامربوط و بازطراحی است. اصلی‌ترین هدف از پیش‌پردازش، بهبود کیفیت داده‌ها برای افزایش دقت و کارایی مدل‌های تحلیلی و یادگیری ماشین می‌باشد.

چرا نیاز به پیش‌ پردازش داریم؟

پیش‌پردازش داده‌ها مرحله‌ای حیاتی در فرآیند یادگیری ماشین است که به منظور آماده‌سازی داده‌های خام برای تحلیل و مدل‌سازی انجام می‌شود. این فرآیند شامل مجموعه‌ای از تکنیک‌ها و روش‌هاست که هدف آن تبدیل داده‌های نامنظم و غیرقابل استفاده به فرمتی ساختارمند و تمیز است. بدون پیش‌پردازش مناسب، داده‌ها ممکن است شامل خطاها، مقادیر گمشده، نویز و ناسازگاری‌هایی باشند که می‌توانند دقت و کارایی مدل‌های یادگیری ماشین را تحت تأثیر قرار دهند. بنابراین، پیش‌پردازش نه تنها به افزایش کیفیت داده‌ها کمک می‌کند بلکه بهبود عملکرد مدل‌ها و نتایج نهایی را نیز تضمین می‌کند.

مراحل پیش‌ پردازش داده‌ ها در پایتون

برای پیش پردازش داده ها در یادگیری ماشین با پایتون چهار مرحله اصلی وجود دارد. این مراحل عبارتند از:

• تقسیم مجموعه‌داده به دو بخش آموزشی و آزمایشی
• تحلیل داده‌های گمشده
• تحلیل ویژگی‌های طبقه‌بندی شده
• نرمال‌سازی مجموعه‌داده

توجه داشته باشید که تقسیم مجموعه‌داده به دو بخش آموزشی و آزمایشی  اولین گام در این فرآیند است. در این مرحله داده‌ها به دو قسمت تقسیم می‌شوند تا مدل بر روی داده‌های آموزشی، آموزش ببیند و سپس بر روی داده‌های آزمایشی ارزیابی شود. این کار به جلوگیری از بیش‌برازش (overfitting) کمک کرده و اطمینان می‌دهد که مدل توانایی تعمیم به داده‌های جدید را دارد. در گام بعدی داده‌های گمشده بررسی می‌شوند. این مرحله شامل شناسایی و اصلاح مقادیر گمشده در مجموعه‌داده است، زیرا وجود داده‌های ناقص می‌تواند بر دقت مدل تأثیر منفی بگذارد. سپس ویژگی‌ها طبقه‌بندی شده بررسی می‌شوند تا اطمینان حاصل شود که داده‌های غیرعدد‌ی به شکل مناسب تبدیل شده‌اند. در مرحله آخر نرمال‌سازی مجموعه‌داده انجام می‌شود تا مقادیر ویژگی‌ها در یک محدوده مشخص قرار گیرند. این مرحله موجب بهبود عملکرد الگوریتم‌ها شده و کمک می‌کند تا مدل‌ها بهتر عمل کنند.

پیش‌ پردازش داده

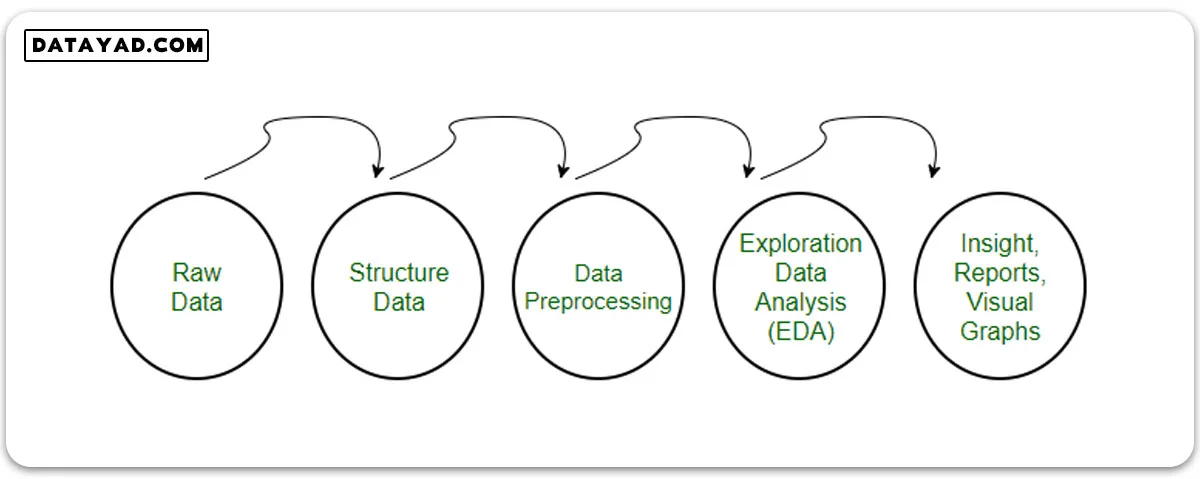
پیش از ارسال داده‌ها به الگوریتم‌ها، تغییرات و اصلاحاتی روی آنها انجام می‌شود که به آن “پیش‌ پردازش” می‌گویند. این مرحله، داده‌های خام را تبدیل به مجموعه‌ای تمیز و قابل استفاده می‌کند، چرا که داده‌ها زمان جمع‌آوری معمولاً به شکل نامنظم و ناپیوسته هستند.

چرا نیاز به پیش‌ پردازش داریم؟

✓ برای دستیابی به نتایج بهتر در پروژه‌های یادگیری ماشین، به شکل و ساختار مناسبی از داده‌ها احتیاج داریم. برخی مدل‌ها نیاز به داده‌هایی با قالب خاص دارند. مثلاً الگوریتم جنگل تصادفی با مقادیر خالی سازگار نیست.

✓ همچنین، ایده‌آل است که داده‌ها به گونه‌ای فرمت‌بندی شوند که بتوان بر روی آن‌ها چندین الگوریتم یادگیری ماشین و یادگیری عمیق را اجرا کرد تا بتوان از بین الگوریتم‌ها بهترین انتخاب را انجام داد.

مراحل پیش‌ پردازش داده‌ ها در پایتون

✓ مرحله اول: کتابخانه‌های مورد نیاز را وارد کنید.

# importing libraries
import pandas as pd
import scipy
import numpy as np
from sklearn.preprocessing import MinMaxScaler
import seaborn as sns
import matplotlib.pyplot as plt

✓ مرحله دوم: داده‌ها را از این لینک بارگیری کنید.

# Load the dataset
df = pd.read_csv('Geeksforgeeks/Data/diabetes.csv')
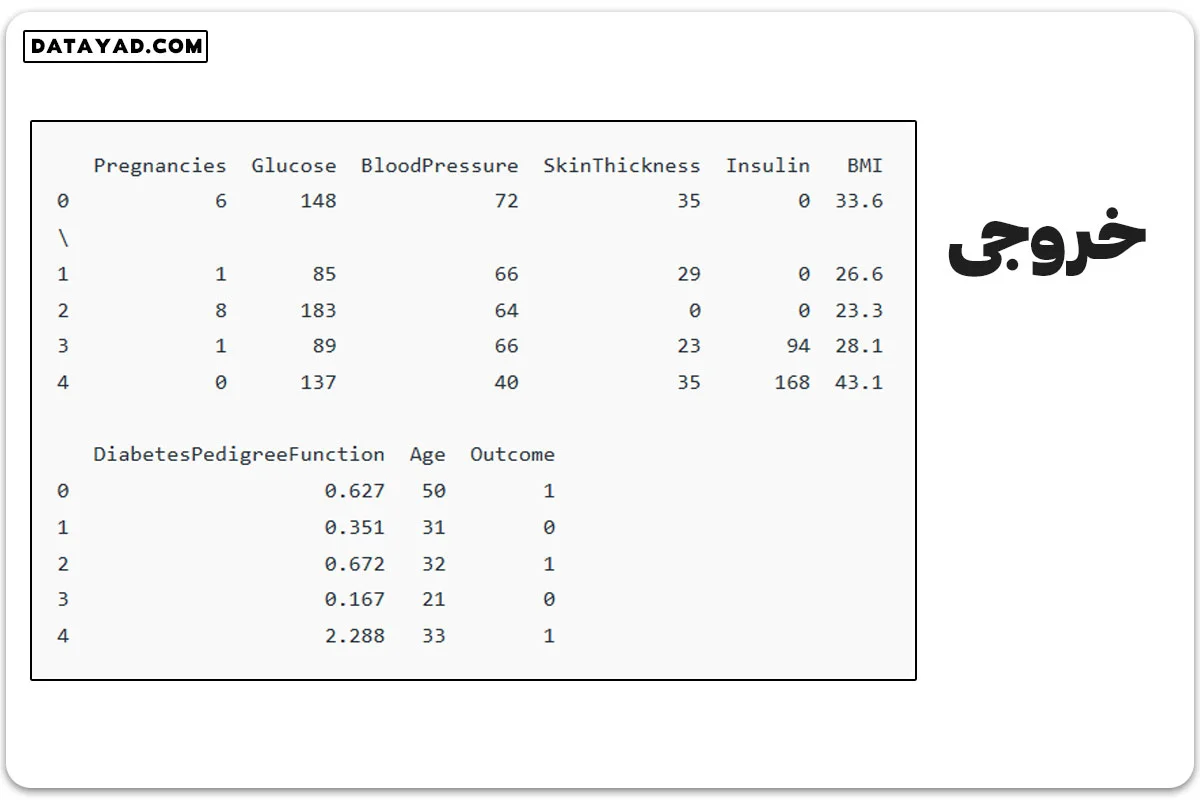
print(df.head())

✓ بررسی داده ها

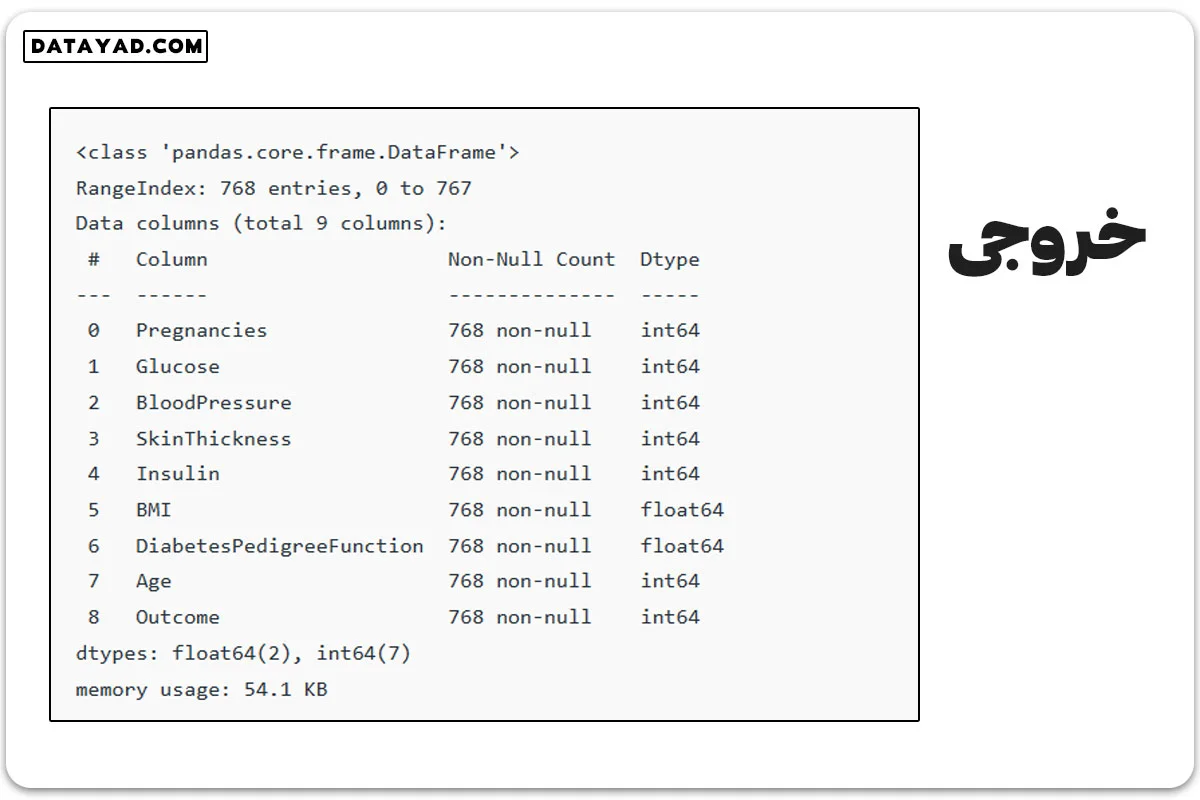
df.info()

بعد از بررسی داده‌ها، متوجه می‌شویم که ۹ ستون داریم و هر ستون ۷۶۸ مقدار است. خوشبختانه، هیچ مقدار خالی‌ای در داده‌ها نیست. البته، با استفاده از دستور ()df.isnull می‌توانیم این موضوع را بررسی کنیم.

df.isnull().sum()

✓ مرحله سوم: تجزیه و تحلیل آماری

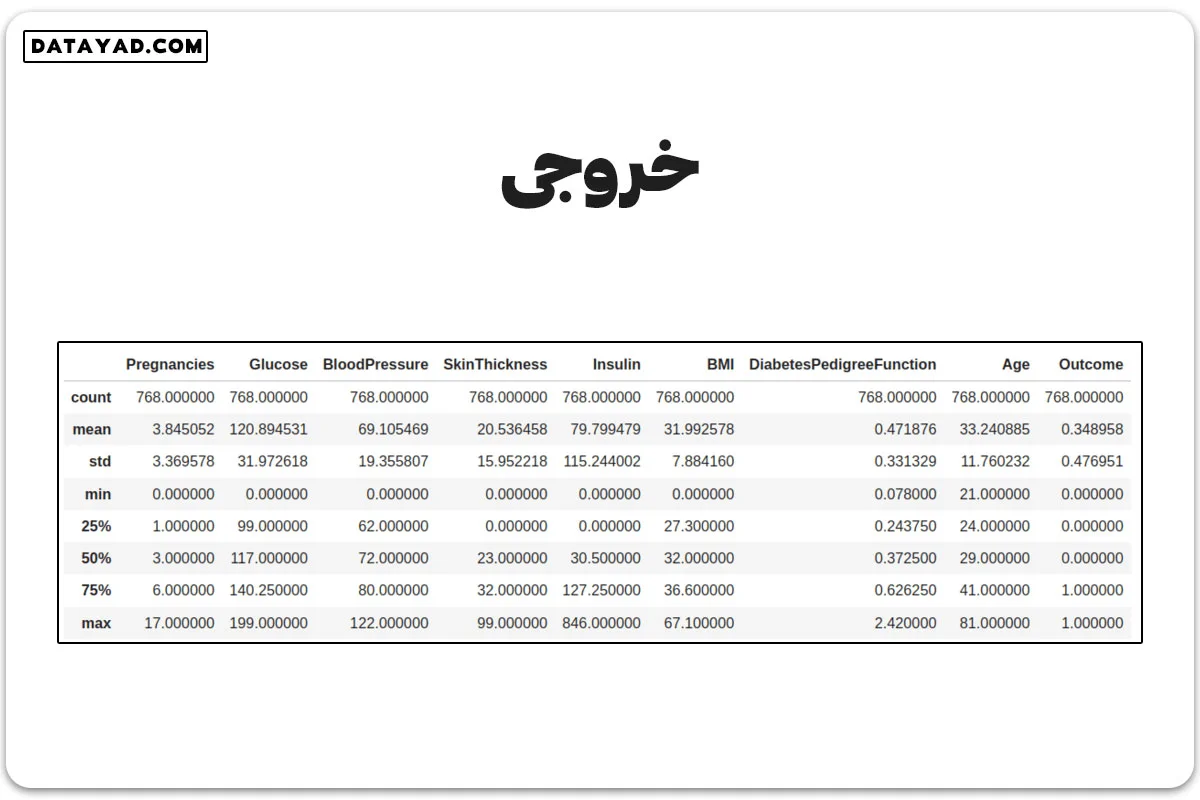
با استفاده از دستور df.describe()، نمای کلی ای از داده‌ها می‌گیریم.

df.describe()

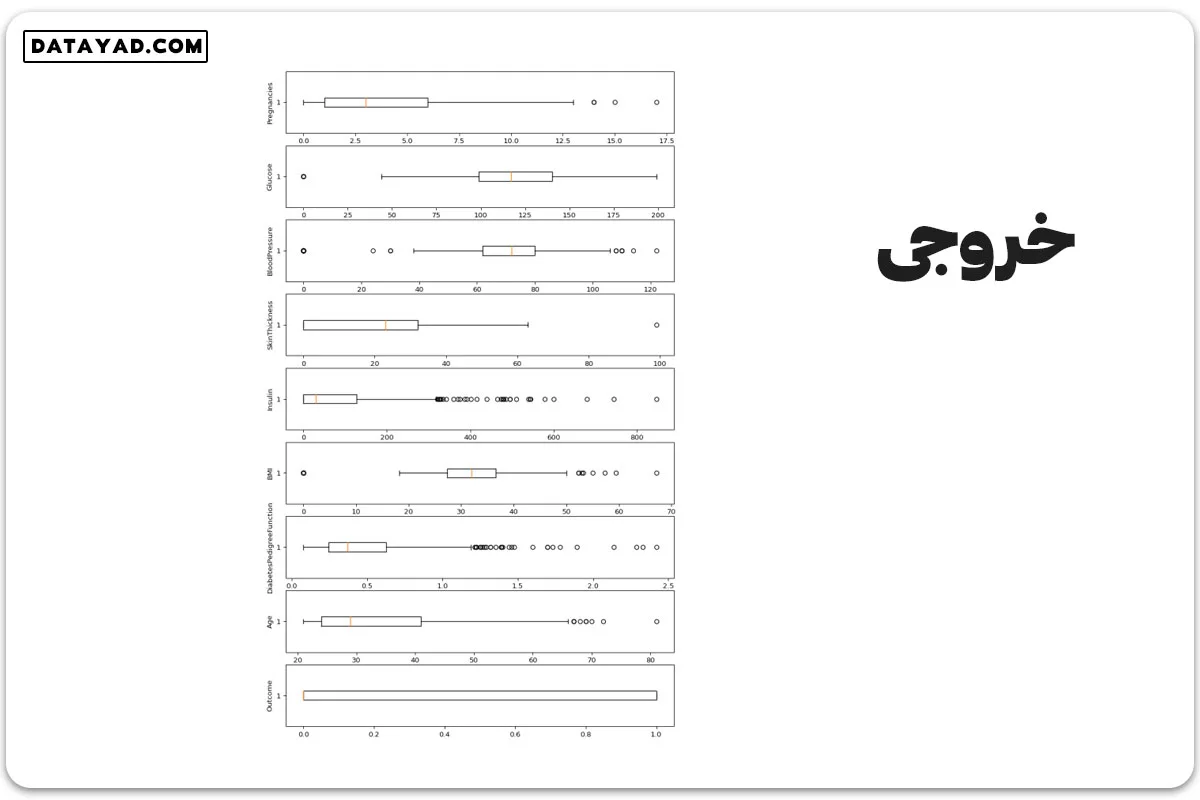
از این جدول، مشاهده می‌کنیم که برخی ستون‌ها مانند انسولین، تعداد بارداری‌ها، شاخص توده‌ی بدن و فشار خون، مقادیر پرت دارند. برای درک بهتر، بهتر است یک نمودار جعبه‌ای برای هر ستون رسم کنیم.

✓ مرحله چهارم: بررسی مقدار پرت

# Box Plots
fig, axs = plt.subplots(9,1,dpi=95, figsize=(7,17))
i = 0
for col in df.columns:
	axs[i].boxplot(df[col], vert=False)
	axs[i].set_ylabel(col)
	i+=1
plt.show()

نمودارها نشان‌دهنده این هستند که تقریباً هر ستونی مقدار پرتی دارد، پس باید آن‌ها را حذف کنیم.

✓ رهاسازی مقدار پرت

# Identify the quartiles
q1, q3 = np.percentile(df['Insulin'], [25, 75])
# Calculate the interquartile range
iqr = q3 - q1
# Calculate the lower and upper bounds
lower_bound = q1 - (1.5 * iqr)
upper_bound = q3 + (1.5 * iqr)
# Drop the outliers
clean_data = df[(df['Insulin'] >= lower_bound) 
				& (df['Insulin'] <= upper_bound)]


# Identify the quartiles
q1, q3 = np.percentile(clean_data['Pregnancies'], [25, 75])
# Calculate the interquartile range
iqr = q3 - q1
# Calculate the lower and upper bounds
lower_bound = q1 - (1.5 * iqr)
upper_bound = q3 + (1.5 * iqr)
# Drop the outliers
clean_data = clean_data[(clean_data['Pregnancies'] >= lower_bound) 
						& (clean_data['Pregnancies'] <= upper_bound)]


# Identify the quartiles
q1, q3 = np.percentile(clean_data['Age'], [25, 75])
# Calculate the interquartile range
iqr = q3 - q1
# Calculate the lower and upper bounds
lower_bound = q1 - (1.5 * iqr)
upper_bound = q3 + (1.5 * iqr)
# Drop the outliers
clean_data = clean_data[(clean_data['Age'] >= lower_bound) 
						& (clean_data['Age'] <= upper_bound)]


# Identify the quartiles
q1, q3 = np.percentile(clean_data['Glucose'], [25, 75])
# Calculate the interquartile range
iqr = q3 - q1
# Calculate the lower and upper bounds
lower_bound = q1 - (1.5 * iqr)
upper_bound = q3 + (1.5 * iqr)
# Drop the outliers
clean_data = clean_data[(clean_data['Glucose'] >= lower_bound) 
						& (clean_data['Glucose'] <= upper_bound)]


# Identify the quartiles
q1, q3 = np.percentile(clean_data['BloodPressure'], [25, 75])
# Calculate the interquartile range
iqr = q3 - q1
# Calculate the lower and upper bounds
lower_bound = q1 - (0.75 * iqr)
upper_bound = q3 + (0.75 * iqr)
# Drop the outliers
clean_data = clean_data[(clean_data['BloodPressure'] >= lower_bound) 
						& (clean_data['BloodPressure'] <= upper_bound)]


# Identify the quartiles
q1, q3 = np.percentile(clean_data['BMI'], [25, 75])
# Calculate the interquartile range
iqr = q3 - q1
# Calculate the lower and upper bounds
lower_bound = q1 - (1.5 * iqr)
upper_bound = q3 + (1.5 * iqr)
# Drop the outliers
clean_data = clean_data[(clean_data['BMI'] >= lower_bound) 
						& (clean_data['BMI'] <= upper_bound)]


# Identify the quartiles
q1, q3 = np.percentile(clean_data['DiabetesPedigreeFunction'], [25, 75])
# Calculate the interquartile range
iqr = q3 - q1
# Calculate the lower and upper bounds
lower_bound = q1 - (1.5 * iqr)
upper_bound = q3 + (1.5 * iqr)

# Drop the outliers
clean_data = clean_data[(clean_data['DiabetesPedigreeFunction'] >= lower_bound) 
						& (clean_data['DiabetesPedigreeFunction'] <= upper_bound)]

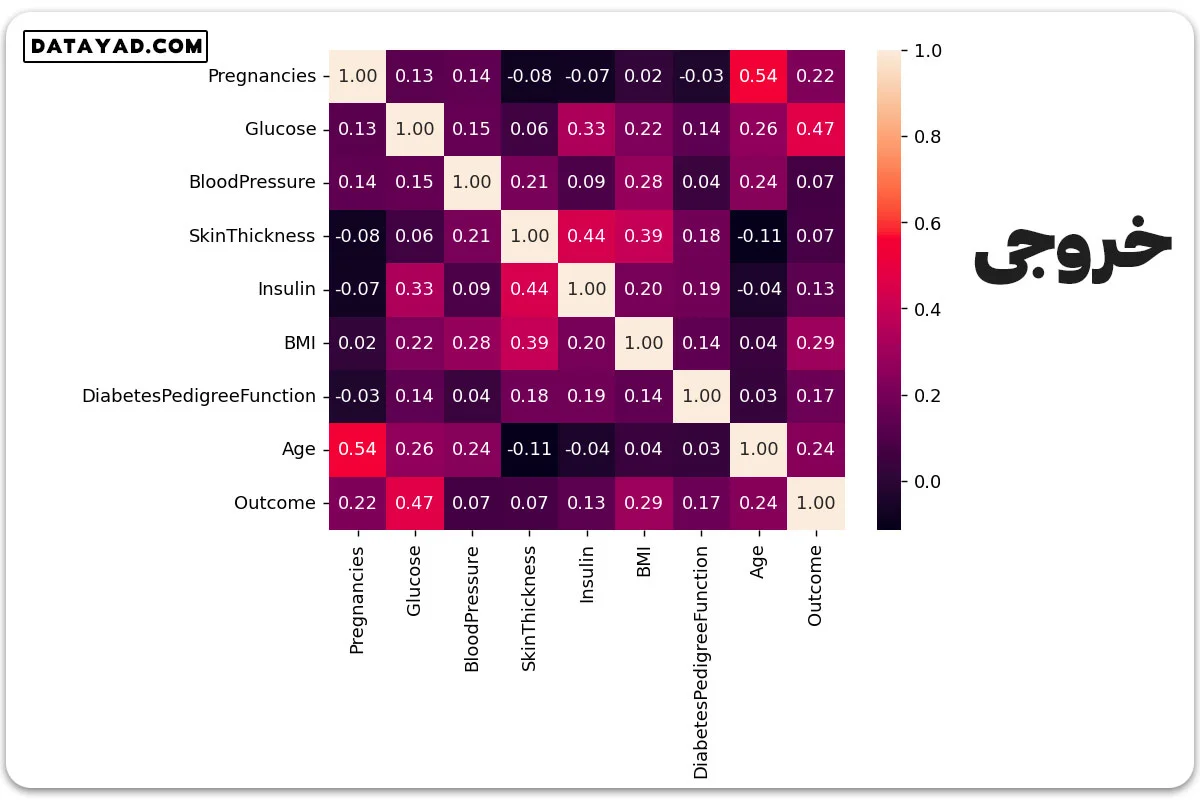
✓ مرحله پنجم: بررسی وابستگی بین داده‌ها

#correlation
corr = df.corr()

plt.figure(dpi=130)
sns.heatmap(df.corr(), annot=True, fmt= '.2f')
plt.show()

✓ مرحله ششم: ویژگی‌ها و هدف‌های مستقل را از هم جدا کنیم.

# separate array into input and output components
X = df.drop(columns =['Outcome'])
Y = df.Outcome

✓ مرحله هفتم: داده‌ها را نرمال یا استاندارد کنیم.

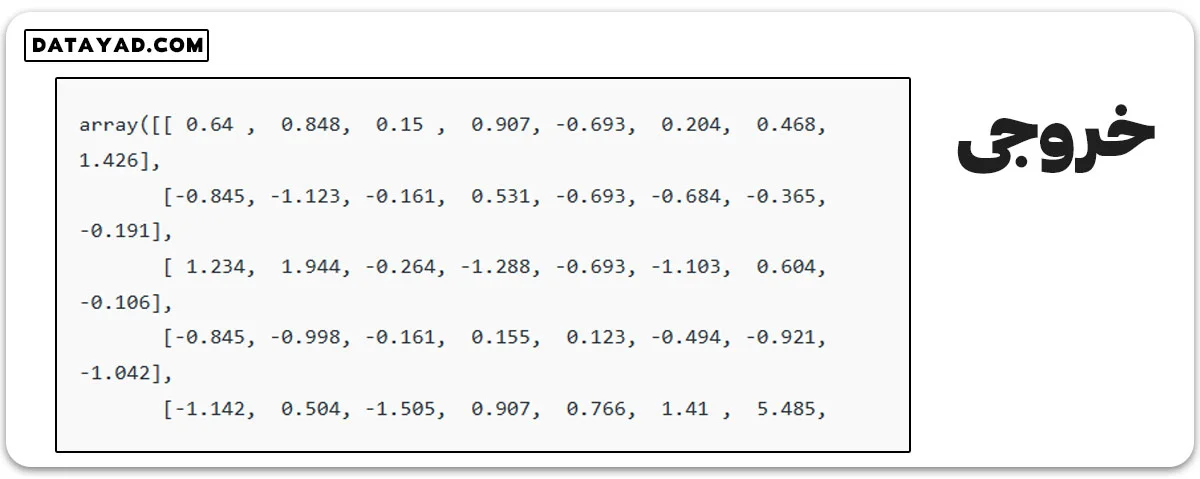
برای نرمال‌سازی، MinMaxScaler را استفاده می‌کنیم تا هر ویژگی در بازه‌ی [0،1] قرار بگیرد. این روش برای ویژگی‌هایی با مقیاس‌های متفاوت و در الگوریتم‌هایی مانند k-NN یا شبکه‌های عصبی مناسب است.

# initialising the MinMaxScaler
scaler = MinMaxScaler(feature_range=(0, 1))

# learning the statistical parameters for each of the data and transforming
rescaledX = scaler.fit_transform(X)
rescaledX[:5]

برای استانداردسازی، از کلاس StandardScaler در scikit-learn استفاده می‌کنیم. این روش وقتی مناسب است که ویژگی‌ها توزیع نرمال دارند یا الگوریتم حساس به مقیاس ویژگی‌ها نیست.

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler().fit(X)
rescaledX = scaler.transform(X)
rescaledX[:5]

سوالات متداول

چرا پیش‌پردازش داده‌ها در یادگیری ماشین اهمیت دارد و چه تأثیری بر عملکرد مدل‌ها دارد؟

پیش‌پردازش داده‌ها به افزایش دقت نتایج تحلیل و کیفیت اطلاعات کمک می‌کند. این مرحله برای طراحی الگوریتم‌های یادگیری ماشین و هوش مصنوعی ضروری است و موجب بهبود روش‌های سازماندهی و پاک‌سازی داده‌ها می‌شود.

چه روش‌هایی برای شناسایی و مدیریت داده‌های گمشده (Missing Data) وجود دارد؟

برای حل مشکل داده‌های گمشده می‌توان از تکنیک‌هایی مانند جایگزینی با میانگین یا میانه استفاده کرد. گزینه‌های دیگر شامل جایگزینی با نمونه‌های تصادفی و روش جایگزینی چندگانه هستند.

استانداردسازی و نرمال‌سازی داده‌ها چه تفاوتی با هم دارند و چه زمانی باید از هرکدام استفاده کرد؟

انتخاب روش مناسب برای پردازش داده‌ها به نوع تحلیل مورد نظر بستگی دارد. در صورتی که هدف مقایسه داده‌ها از منابع مختلف باشد، استانداردسازی بهترین گزینه است، در حالی که نرمال‌سازی برای اطمینان از یکسان بودن قالب داده‌ها مناسب‌تر خواهد بود.

چگونه می‌توان ویژگی‌های غیرمرتبط یا زائد (Irrelevant or Redundant Features) را شناسایی و حذف کرد؟

برای شناسایی و حذف ویژگی‌های غیرمرتبط یا زائد می‌توان از تکنیک‌هایی مانند تحلیل همبستگی و روش‌های انتخاب ویژگی استفاده کرد. این روش‌ها به شناسایی ویژگی‌هایی که تأثیر کمی بر روی هدف دارند یا با سایر ویژگی‌ها تکراری هستند، کمک می‌کنند.