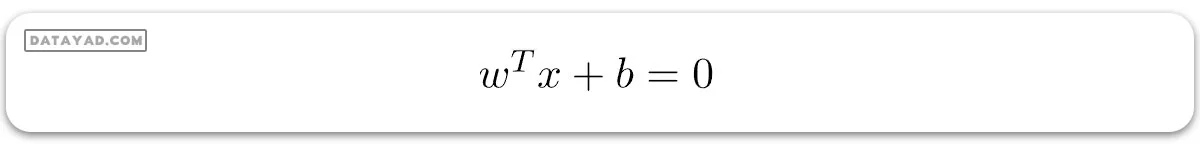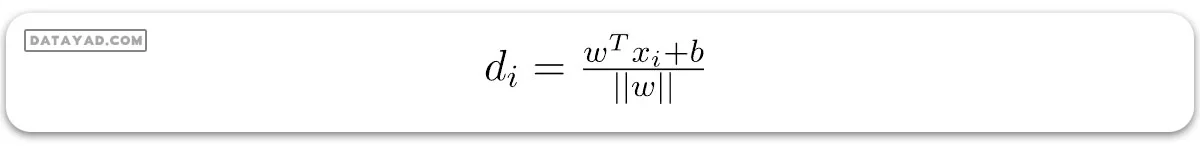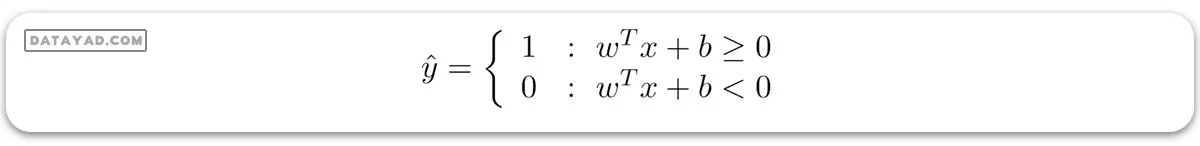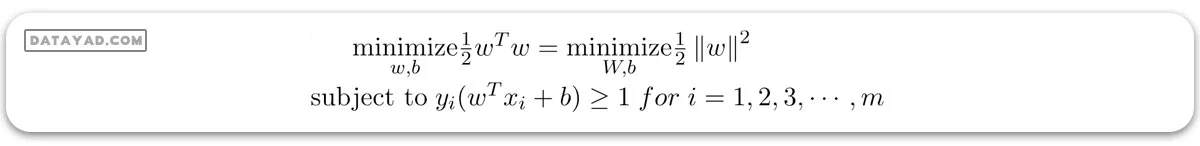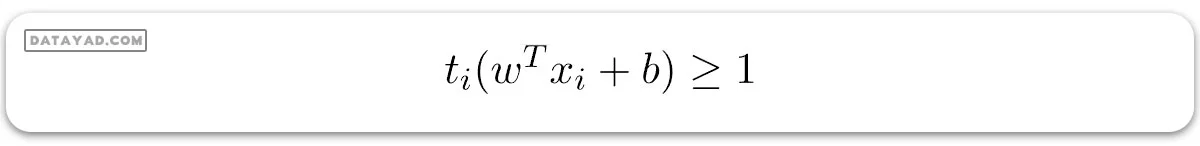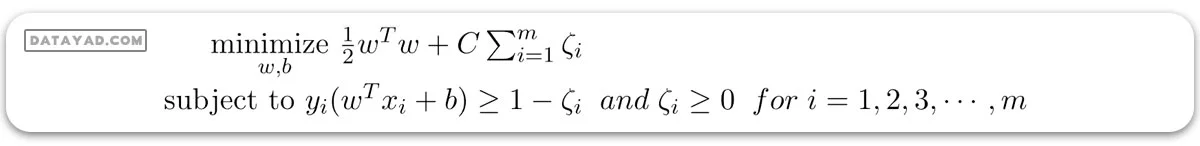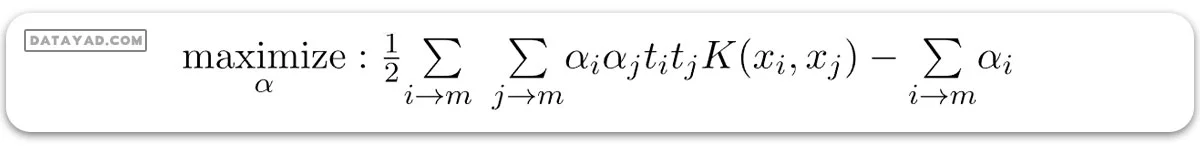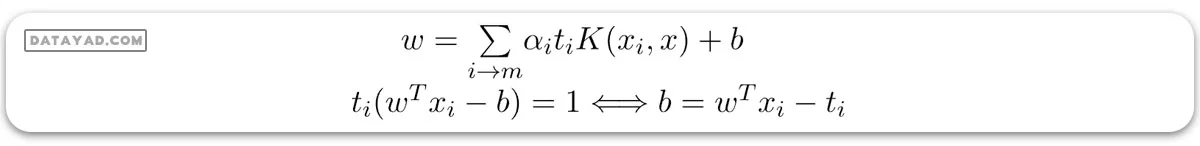الگوریتم ماشین بردار پشتیبان (SVM)

فهرست مطالب
ماشین بردار پشتیبان (SVM) یکی از الگوریتم های یادگیری ماشین قدرتمند است که برای طبقهبندی خطی یا غیرخطی، رگرسیون و حتی تشخیص ناهنجاریها استفاده میشود. SVMها میتوانند برای انواع وظایفی مانند طبقهبندی متن، طبقهبندی تصویر، تشخیص اسپم، شناسایی دستنوشته، تحلیل بیان ژن، تشخیص چهره و تشخیص ناهنجاریها استفاده شوند. SVMها به دلیل تواناییشان در کنارهگیری دادههای با بعد بالا و روابط غیرخطی، در کاربردهای مختلف سازگار و کارآمد هستند. و همچنین با استفاده از SVM برای دستهبندی در یک مجموعه داده غیرخطی میتوان استفاده کرد.
الگوریتمهای SVM بسیار مؤثر هستند زیرا ما در تلاشیم برای یافتن هایپرپلان جداکنندهی حداکثری بین کلاسهای مختلف موجود در ویژگی هدف.
| کرنل | ویژگیها | مزایا | معایب | موارد استفاده |
| خطی (Linear) | – فرض میکند دادهها به صورت خطی جداپذیر هستند | – ساده و سریع | – فقط برای دادههای خطی قابل استفاده است | – دادههایی که به صورت خطی جداپذیر هستند |
| چندجملهای (Polynomial) | – از تابع چندجملهای برای نگاشت دادهها به فضای با ابعاد بالاتر استفاده میکند | – انعطافپذیرتر از کرنل خطی | – تنظیم پارامترهای آن (درجه و ضریب) ممکن است دشوار باشد | – دادههایی که نیاز به نگاشت غیرخطی دارند اما ساختار سادهای دارند |
| RBF (شعاعی) | – از تابع گاوسی برای نگاشت دادهها به فضای با ابعاد بالاتر استفاده میکند | – بسیار انعطافپذیر و قدرتمند برای دادههای پیچیده | – ممکن است به بیشبرازش (Overfitting) منجر شود | – دادههای پیچیده و غیرخطی که ساختار مشخصی ندارند |
| سیگموئید (Sigmoid) | – از تابع سیگموئید برای نگاشت دادهها استفاده میکند | – میتواند برای برخی دادهها عملکرد خوبی داشته باشد | – ممکن است برای دادههای خاص عملکرد ضعیفی داشته باشد | – دادههایی که ساختار شبیه به شبکههای عصبی دارند |

ماشین بردار پشتیبان (SVM)
ماشین بردار پشتیبان (SVM) یک الگوریتم یادگیری ماشین نظارتی است که هم برای طبقهبندی و هم برای رگرسیون استفاده میشود. هرچند که ما در مورد مسائل رگرسیون نیز صحبت میکنیم، اما این الگوریتم بیشتر برای طبقهبندی مناسب است.
هدف اصلی الگوریتم SVM، یافتن یک هایپرپلان بهینه در یک فضای N-بعدی است که بتواند نقاط دادهها را در کلاسهای مختلف در فضای ویژگی جدا کند. هایپرپلان تلاش میکند که فاصله بین نزدیکترین نقاط کلاسهای مختلف به حداکثر ممکن برسد.
ابعاد هایپرپلان بستگی به تعداد ویژگیها دارد. اگر تعداد ویژگیهای ورودی دو باشد، آنگاه هایپرپلان فقط یک خط است. اگر تعداد ویژگیهای ورودی سه باشد، آنگاه هایپرپلان به یک صفحه 2-بعدی تبدیل میشود. وقتی تعداد ویژگیها از سه فراتر رود، تصور آن دشوار میشود.
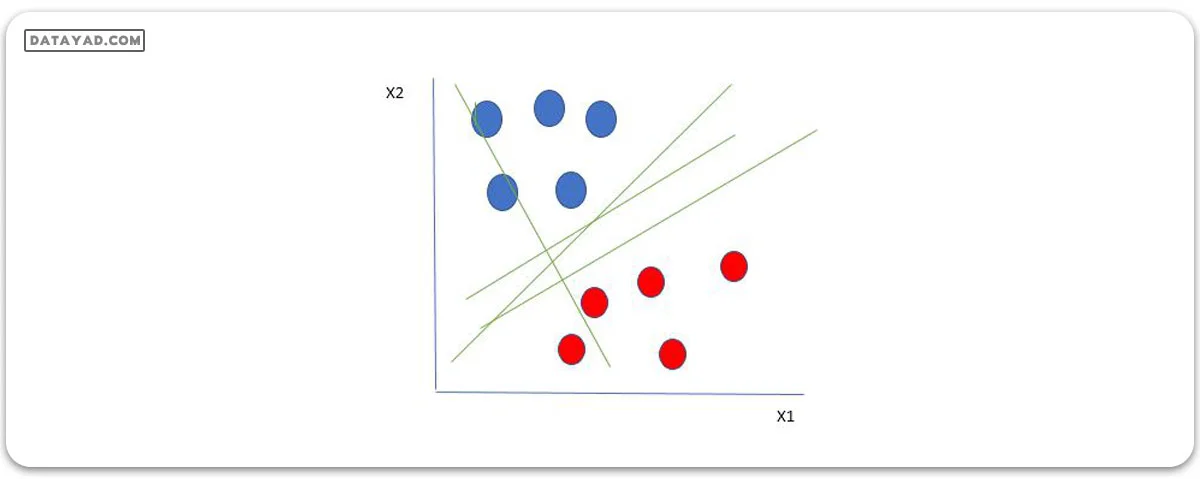
بیایید دو متغیر مستقل x1 و x2 و یک متغیر وابسته که یا یک دایره آبی یا یک دایره قرمز است را در نظر بگیریم.
از شکل بالا بسیار واضح است که چندین خط (هایپرپلان ما در اینجا یک خط است زیرا ما فقط دو ویژگی ورودی x1 و x2 را در نظر میگیریم) وجود دارند که نقاط دادههای ما را جدا میکنند یا طبقهبندی بین دایرههای قرمز و آبی انجام میدهند. پس چگونه میتوانیم بهترین خط یا به طور کلی بهترین هایپرپلانی را که نقاط دادههای ما را جدا میکند، انتخاب کنیم؟

چگونه SVM کار میکند؟
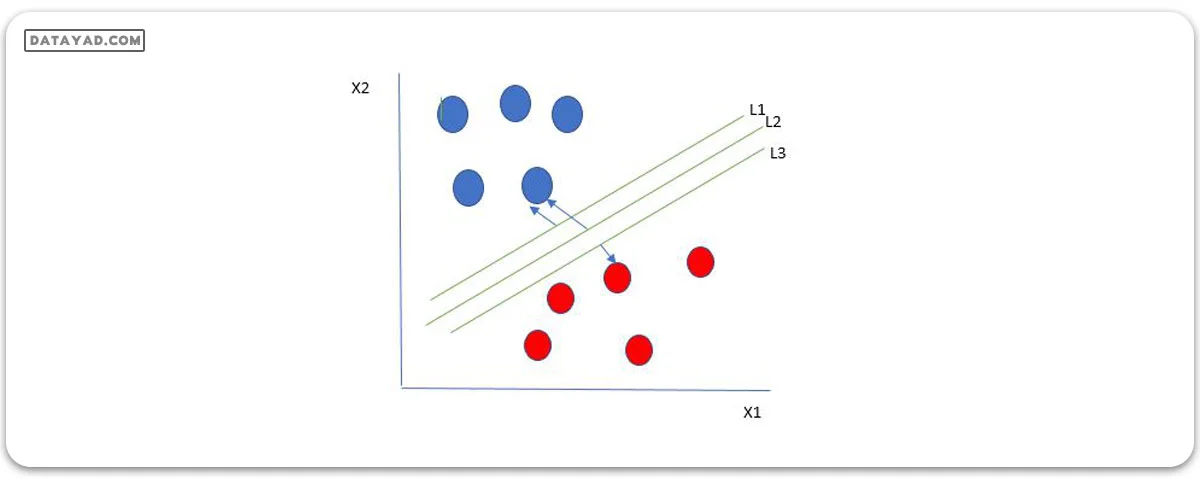
یک انتخاب منطقی به عنوان بهترین هایپرپلان، آن است که بیشترین جدایی یا حاشیه را بین دو کلاس نمایندگی کند.
بنابراین ما هایپرپلانی را انتخاب میکنیم که فاصله آن از نزدیکترین نقطه داده در هر طرف، بیشترین میزان باشد. اگر چنین هایپرپلانی وجود داشته باشد، به آن هایپرپلان حاشیهی حداکثری/حاشیه سخت شناخته میشود. پس از شکل بالا، ما L2 را انتخاب میکنیم. بیایید یک سناریویی مانند زیر را در نظر بگیریم.
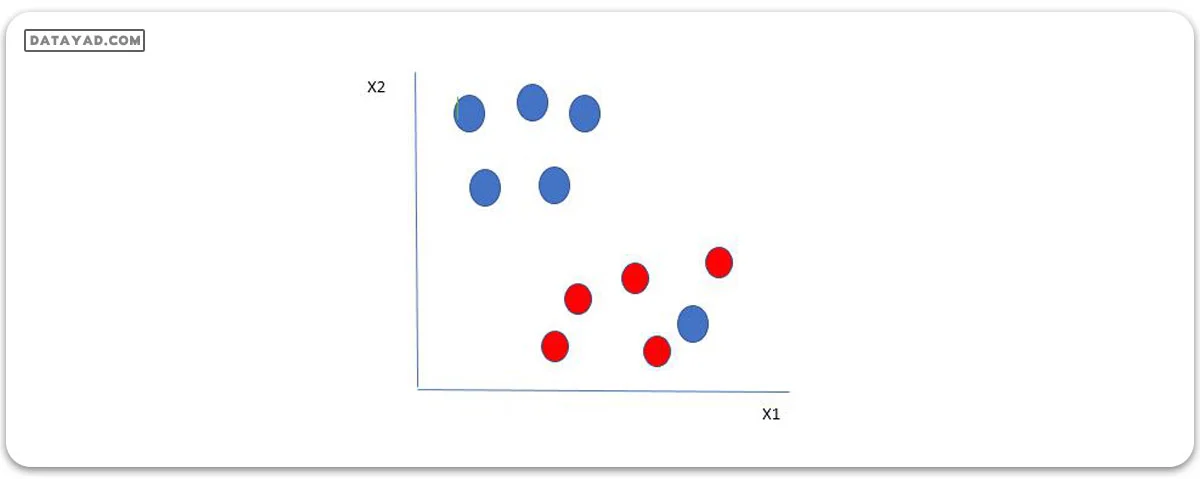
در اینجا ما یک توپ آبی در مرز توپهای قرمز داریم. پس SVM چگونه دادهها را طبقهبندی میکند؟ ساده است! توپ آبی در مرز توپهای قرمز یک ناهنجاری برای توپهای آبی است. الگوریتم SVM ویژگی نادیده گرفتن ناهنجاریها و یافتن بهترین هایپرپلانی که حاشیه را بیشینه میکند را دارد. SVM نسبت به ناهنجاریها مقاوم است.
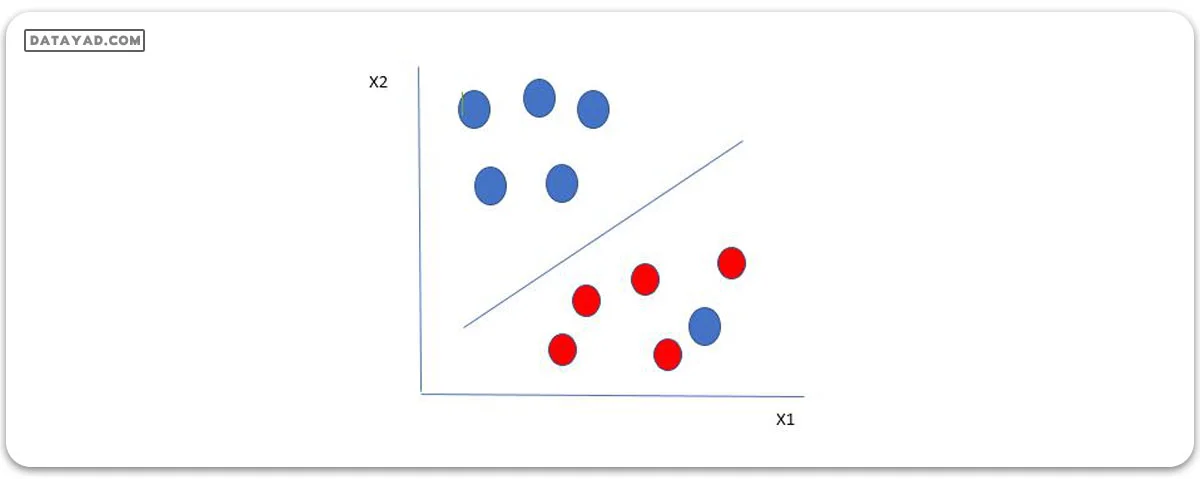
در این نوع دادهها، SVM بیشترین فاصله ممکن را مانند دادههای قبلی پیدا میکند، و همزمان برای هر بار که نقطهای از حاشیه عبور میکند، جریمهای در نظر میگیرد. به همین دلیل، در این موارد به حاشیهها “حاشیههای نرم” گفته میشود.
وقتی حاشیهی نرم برای مجموعه دادهها وجود دارد، SVM سعی میکند مجموعهی زیر را کاهش دهد.
(1/margin+∧(∑penalty))
اتلاف هینج (Hinge loss)، یک نوع جریمه رایج است. اگر تخلفی نباشد، هیچ اتلاف هینجی وجود ندارد. در صورت وجود تخلفات، اتلاف هینج متناسب با فاصلهی تخلف خواهد بود.
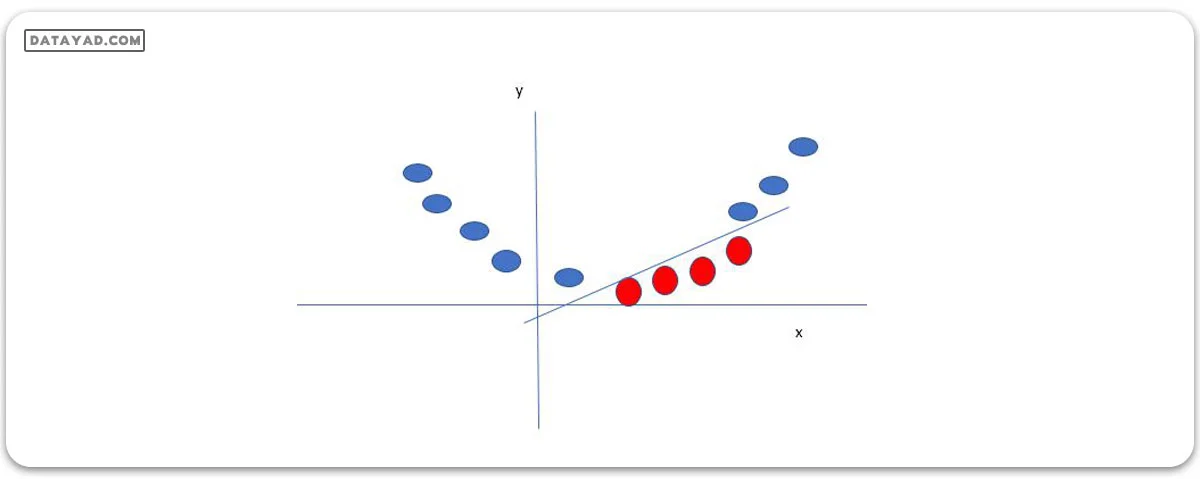
تا به حال، ما در مورد دادههایی صحبت کردیم که به صورت خطی جدا میشوند (مثلا گروههای توپهای آبی و قرمز که با یک خط مستقیم قابل جداسازی هستند). اما اگر دادهها به صورت خطی جدا نشوند، چه باید کرد؟
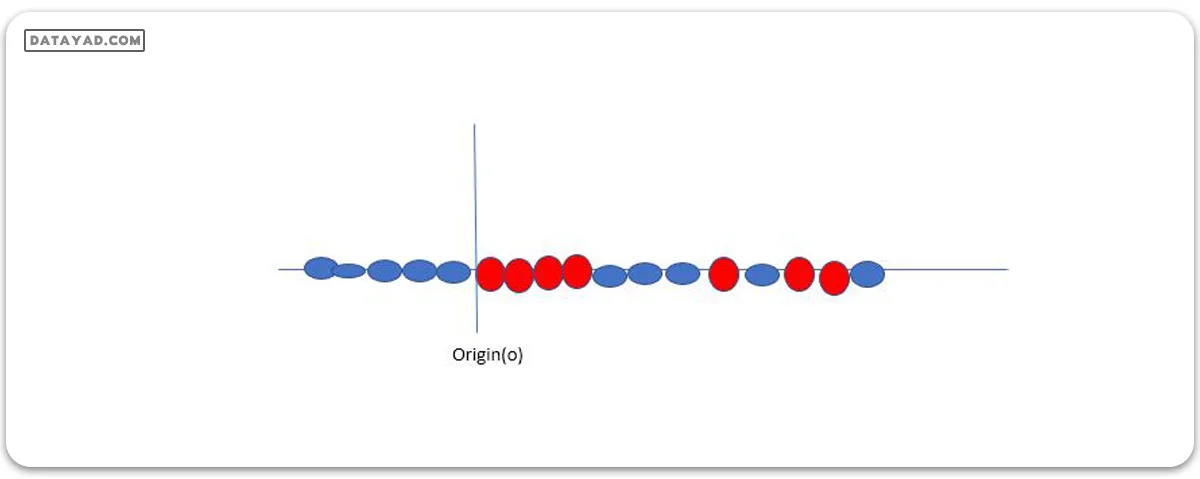
فرض کنید دادههای ما در شکل بالا نشان داده شدهاند. SVM این مسئله را با ایجاد یک متغیر جدید با استفاده از یک کرنل حل میکند. ما به نقطهای به نام xi روی خط اشاره میکنیم و یک متغیر جدید yi را به عنوان تابعی از فاصله تا مبدأ o ایجاد میکنیم. پس اگر این را نمایش دهیم، چیزی شبیه به آنچه در زیر نشان داده شده است، به دست میآوریم.
در این حالت، متغیر جدید y به عنوان تابعی از فاصله تا مبدأ ایجاد میشود. یک تابع غیرخطی که یک متغیر جدید ایجاد میکند، به عنوان یک کرنل شناخته میشود.
اصطلاحات ماشین بردار پشتیبان
1. هایپرپلان: هایپرپلان مرز تصمیمگیری است که برای جداسازی نقاط دادههای کلاسهای مختلف در فضای ویژگی استفاده میشود. در مورد طبقهبندیهای خطی، این یک معادله خطی خواهد بود، یعنی wx+b = 0.
2. بردارهای پشتیبان: بردارهای پشتیبان نزدیکترین نقاط داده به هایپرپلان هستند که نقش حیاتی در تعیین هایپرپلان و حاشیه دارند.
3. حاشیه: حاشیه فاصله بین بردار پشتیبان و هایپرپلان است. هدف اصلی الگوریتم ماشین بردار پشتیبان بیشینه کردن حاشیه است. حاشیه وسیعتر نشان دهنده عملکرد بهتر طبقهبندی است.
4. کرنل: کرنل یک تابع ریاضی است که در SVM برای تصویرکردن نقاط داده ورودی اصلی به فضاهای ویژگی با بعد بالا استفاده میشود، به طوری که هایپرپلان حتی اگر نقاط داده در فضای ورودی اصلی به صورت خطی جداپذیر نباشند، به راحتی پیدا شود. برخی از توابع کرنل رایج عبارتند از خطی، چندجملهای، تابع پایه شعاعی (RBF) و سیگموئید.
5. حاشیه سخت: هایپرپلان حاشیه حداکثر یا هایپرپلان حاشیه سخت، هایپرپلانی است که نقاط داده مختلف را بدون هیچ طبقهبندی اشتباهی به درستی جدا میکند.
6. حاشیه نرم: وقتی دادهها به طور کامل جداپذیر نیستند یا حاوی ناهنجاریها هستند، SVM از تکنیک حاشیه نرم استفاده میکند. هر نقطه داده یک متغیر ارتجاعی توسط فرمولبندی SVM با حاشیه نرم معرفی میشود که نیاز به حاشیه سخت را نرم میکند و اجازه برخی طبقهبندیهای اشتباه یا تخلفات را میدهد. این روش بین افزایش حاشیه و کاهش تخلفات تعادل ایجاد میکند.
7. C: پارامتر تنظیم C در SVM، بیشینهسازی حاشیه و جریمههای طبقهبندی اشتباه را متعادل میکند. این پارامتر تعیین میکند که جریمه برای عبور از حاشیه یا طبقهبندی اشتباه چقدر باشد. با افزایش مقدار C، جریمه سختتری اعمال میشود که منجر به حاشیه کوچکتر و احتمالاً طبقهبندی اشتباه کمتر میشود.
8. اتلاف هینج: اتلاف هینج یک تابع ضرر معمول در SVMها است. این تابع طبقهبندیهای اشتباه یا تخلفات حاشیه را جریمه میکند. تابع هدف در SVM اغلب با ترکیب این تابع با شرط تنظیم شکل میگیرد.
9. مسئله دوگانه: مسئله دوگانه مسئله بهینهسازی است که نیاز به یافتن ضرایب لاگرانژ مرتبط با بردارهای پشتیبان دارد و میتواند برای حل SVM استفاده شود. فرمولبندی دوگانه امکان استفاده از ترفندهای کرنل و محاسبات کارآمدتر را فراهم میکند.

چرا SVM یکی از محبوبترین الگوریتمهای یادگیری ماشین است؟
ماشین بردار پشتیبان یا SVM یکی از محبوبترین الگوریتمهای ماشین لرنینگ است، زیرا توانایی زیادی در مدیریت مسائل طبقهبندی و رگرسیون، در دادههای با ابعاد بالا دارد. این الگوریتم با استفاده از کرنلهای مختلف (مانند خطی، چندجملهای، RBF و سیگموئید) میتواند دادههای خطی و غیرخطی را بهطور مؤثر جدا کند. یکی از نقاط قوت SVM، تمرکز آن روی حاشیهی بیشینه (Maximal Margin) است که به مدل کمک میکند تا تعمیمپذیری بهتری داشته و از بیشبرازش (Overfitting) جلوگیری کند. همچنین SVM به دلیل پشتیبانی از دادههای با ابعاد بالا و عملکرد قوی در مسائل پیچیده، در حوزههایی مانند پردازش تصویر، تشخیص متن و بیوانفورماتیک بسیار مورد استفاده قرار میگیرد. این ویژگیها باعث شدهاند SVM بهعنوان یکی از الگوریتمهای طبقهبندی قدرتمند و پرکاربرد در یادگیری ماشین شناخته شود. اگر قصد آشنایی با جبر خطی در یادگیری ماشین را دارید، میتوانید مقاله ما را مطالعه کنید.
بیان ریاضی ماشین بردار پشتیبان
یک مسئله طبقهبندی دودویی با دو کلاس، که با +1 و -1 برچسبگذاری شدهاند، در نظر بگیرید. ما یک مجموعه داده آموزشی شامل بردارهای ویژگی ورودی X و برچسبهای کلاس متناظر Y داریم.
معادله برای هایپرپلان خطی میتواند به صورت زیر نوشته شود:
بردار W نشان دهنده بردار عمود بر هایپرپلان است، یعنی جهتی عمود بر هایپرپلان. پارامتر b در معادله نشان دهنده offset یا فاصله هایپرپلان از مبدأ در امتداد بردار عمود w است.
فاصله بین یک نقطه داده xi و مرز تصمیمگیری میتواند به صورت زیر محاسبه شود:
که در آن ||w|| نشان دهنده نُرم اقلیدسی بردار وزن w است. نرم اقلیدسی بردار عمود W
برای طبقهبند SVM خطی:
بهینهسازی
– برای طبقهبند SVM خطی با حاشیه سخت:
متغیر هدف یا برچسب برای ith امین نمونه آموزشی با نماد ti در این بیانیه نشان داده شده است و ti = -1 برای موارد منفی (وقتی yi = 0) و (ti = 1) برای موارد مثبت (وقتی yi = 1) به ترتیب. زیرا ما به مرز تصمیمگیری نیاز داریم که محدودیت زیر را برآورده کند:
– برای طبقهبند SVM خطی با حاشیه نرم:
– مسئله دوگانه: مسئله دوگانه مسئله بهینهسازی است که نیاز به یافتن ضرایب لاگرانژ مرتبط با بردارهای پشتیبان دارد و میتواند برای حل SVM استفاده شود. ضرایب لاگرانژ بهینه \(α(i)\) که تابع هدف دوگانه زیر را بیشینه میکنند:
که در آن،
– αi ضریب لاگرانژ مرتبط با ithامین نمونه آموزشی است.
k(xi,xj) تابع کرنل است که شباهت بین دو نمونه xi و xj را محاسبه میکند. این امکان را به SVM میدهد تا با نگاشت ضمنی نمونهها به یک فضای ویژگی با بعد بالاتر، مسائل طبقهبندی غیرخطی را مدیریت کند.
– اصطلاح αi∑ نماینده جمع همه ضرایب لاگرانژ است.
مرز تصمیمگیری SVM میتواند از نظر این ضرایب لاگرانژ بهینه و بردارهای پشتیبان توصیف شود، پس از حل مسئله دوگانه و یافتن ضرایب لاگرانژ بهینه. نمونههای آموزشی که αi > 0 هستند بردارهای پشتیبان میباشند، در حالی که مرز تصمیمگیری توسط فرمول زیر ارائه میشود:
انواع ماشین بردار پشتیبان
بر اساس ماهیت مرز تصمیمگیری، ماشینهای بردار پشتیبان (SVM) به دو بخش اصلی تقسیم میشوند:
SVM خطی
SVMهای خطی از یک مرز تصمیمگیری خطی برای جدا کردن نقاط داده کلاسهای مختلف استفاده میکنند. وقتی دادهها به صورت دقیق خطی جداپذیر هستند، SVMهای خطی بسیار مناسب هستند. این به معنای آن است که یک خط مستقیم تکی (در 2 بعد) یا یک هایپرپلان (در ابعاد بالاتر) میتواند به طور کامل نقاط داده را به کلاسهای مربوط به خود تقسیم کند. یک هایپرپلان که حاشیه بین کلاسها را بیشینه میکند، مرز تصمیمگیری است.
SVM غیرخطی
SVM غیرخطی میتواند برای طبقهبندی دادهها زمانی که نمیتوان آنها را به وسیله یک خط مستقیم (دو بعدی) به دو کلاس تقسیم کرد، استفاده شود. با استفاده از توابع کرنل، SVMهای غیرخطی میتوانند دادههای غیرخطی جداپذیر را مدیریت کنند. دادههای ورودی اصلی توسط این توابع کرنل به فضای ویژگی با بعد بالاتر تبدیل میشوند، جایی که نقاط داده میتوانند به صورت خطی جدا شوند. یک SVM خطی برای یافتن یک مرز تصمیمگیری غیرخطی در این فضای تغییر یافته استفاده میشود.

توابع کرنل محبوب در SVM
کرنل SVM یک تابع است که فضای ورودی با بعد پایین را میگیرد و آن را به فضای با بعد بالاتر تبدیل میکند، یعنی مشکلات غیرقابل جداسازی را به مشکلات قابل جداسازی تبدیل میکند. این امر بیشتر در مشکلات جداسازی غیرخطی مفید است. به زبان ساده، کرنل، تحولات بسیار پیچیدهای بر دادهها انجام میدهد و سپس فرآیندی را برای جداسازی دادهها بر اساس برچسبها یا خروجیهای تعریف شده پیدا میکند.
کاربردهای عملی ماشین بردار پشتیبان
ماشین بردار پشتیبان در مسائل طبقهبندی و رگرسیون کاربرد دارد و در حوزههایی که دادهها دارای ابعاد بالا یا ساختار پیچیده هستند، دارای عملکرد قدرتمندی است. از جمله کاربردهای عملی آن میتوان به تشخیص تصویر (مانند تشخیص چهره و دستخط)، پردازش زبان طبیعی (مانند طبقهبندی متن و تحلیل احساسات)، بیوانفورماتیک (مانند پیشبینی ساختار پروتئین و تشخیص ژن)، تشخیص ناهنجاریها در دادهها (مانند شناسایی تقلب در تراکنشهای مالی) و پزشکی (مانند تشخیص بیماریها بر اساس دادههای پزشکی) اشاره کرد. توانایی SVM در مدیریت دادههای غیرخطی با استفاده از کرنلهای مختلف و تعمیمپذیری بالا، آن را به یکی از ابزارهای قدرتمند در یادگیری ماشین تبدیل کرده است. در ادامه این کاربردهای عملی ماشین بردار را شرح میدهیم. با مطالعه دوره های برنامه نویسی میتوانید اطلاعات بیشتری در این زمینه به دست آورید.
تشخیص تصویر و پردازش تصویر
ماشین بردار پشتیبان در حوزهی تشخیص تصویر و پردازش تصویر کاربرد زیادی دارد. این الگوریتم با استفاده از کرنلهای مناسب مانند RBF، قادر است ویژگیهای پیچیدهی تصاویر را استخراج کرده و آنها را بهطور دقیق طبقهبندی کند. از کاربردهای عملی آن میتوان به تشخیص چهره، شناسایی پلاک خودرو، تشخیص دستنوشته (OCR) و حتی تحلیل تصاویر ماهوارهای اشاره کرد. SVM با توانایی بالا در مدیریت دادههای غیرخطی و ابعاد بالا، یکی از ابزارهای قدرتمند در پردازش تصویر است.
استفاده از SVM در تشخیص اشیا و طبقهبندی تصاویر
ماشین بردار پشتیبان در تشخیص اشیا و طبقهبندی تصاویر کاربرد گستردهای دارد. این ماشین بردار با استفاده از کرنلهای مناسب مانند RBF، میتواند ویژگیهای پیچیدهی تصاویر را استخراج کرده و آنها را بهطور دقیق طبقهبندی کند. این روش در سیستمهای تشخیص چهره، شناسایی پلاک خودرو و حتی تشخیص اشیا در تصاویر ماهوارهای به کار میرود. اگر نیاز به کسب اطلاعات بیشتر در زمینه ماشین لرنینگ دارید، میتوانید یادگیری نظارت شده و بدون نظارت را مطالعه کنید.
مثال عملی: تشخیص دستنوشته با SVM
در تشخیص دستنوشته، ماشین بردار پشتیبان با استفاده از ویژگیهای استخراجشده از تصاویر (مانند پیکسلها یا الگوهای لبهها)، اعداد یا حروف دستنوشته را طبقهبندی میکند. این روش در سیستمهای تشخیص نوری کاراکتر (OCR) و دیجیتالیکردن اسناد دستنویس استفاده میشود. با خواندن کاربرد ماشین لرنینگ میتوانید کارایی ماشین بردار را بهتر درک کنید.
طبقهبندی متن و تحلیل احساسات
ماشین بردار پشتیبان در حوزهی طبقهبندی متن و تحلیل احساسات بهطور گسترده کاربرد دارد. این الگوریتم با تبدیل متن به بردارهای عددی (مانند TF-IDF یا Word Embedding)، قادر است متنها را بر اساس محتوا یا احساسات (مثبت، منفی، خنثی) طبقهبندی کند. از کاربردهای عملی آن میتوان به تحلیل احساسات نظرات کاربران در شبکههای اجتماعی، بررسی بازخورد محصولات و فیلتر کردن ایمیلهای اسپم اشاره کرد. SVM با دقت بالا و توانایی مدیریت دادههای با ابعاد زیاد، ابزاری مؤثر در پردازش زبان طبیعی و تحلیل متن شناخته میشود.

کاربرد SVM در تحلیل احساسات (Sentiment Analysis)
ماشین بردار پشتیبان در تحلیل احساسات متنها، مانند نظرات کاربران در شبکههای اجتماعی یا بررسی محصولات مورد استفاده قرار میگیرد. با تبدیل متن به بردارهای عددی (مانند TF-IDF یا Word Embedding)، SVM میتواند احساسات مثبت، منفی یا خنثی را با دقت بالا تشخیص دهد.
طبقهبندی اسپم و غیراسپم با SVM
SVM در فیلتر کردن ایمیلهای اسپم نیز کاربرد دارد. همچنین با استفاده از ویژگیهای متن مانند کلمات کلیدی یا الگوهای متنی، میتواند ایمیلهای اسپم را از غیراسپم بهطور مؤثر جدا کند.
پیشبینی و تحلیل دادهها
ماشین بردار پشتیبان در پیشبینی و تحلیل دادهها مورد استفاده قرار میگیرد. این الگوریتم با توانایی بالا در مدیریت دادههای پیچیده و غیرخطی، برای پیشبینی روندهای مالی (مانند قیمت سهام یا تشخیص الگوهای معاملاتی)، تحلیل دادههای پزشکی (مانند تشخیص بیماریها بر اساس تصاویر MRI یا آزمایشهای خون) و حتی پیشبینی رفتار مشتریان در بازاریابی کاربرد دارد. SVM با استفاده از کرنلهای مختلف و تمرکز بر بیشینهکردن حاشیهی تصمیمگیری، دقت و قابلیت تعمیمپذیری بالایی را در پیشبینیها ارائه میدهد.
استفاده از SVM در پیشبینی مالی و بازار بورس
در حوزهی مالی، ماشین بردار پشتیبان برای پیشبینی روند بازار، قیمت سهام یا تشخیص الگوهای معاملاتی استفاده میشود. با تحلیل دادههای تاریخی و شناسایی الگوهای پیچیده، SVM به سرمایهگذاران کمک میکند تا تصمیمات بهتری بگیرند. حال اگر به دنبال یادگیری عمیقتر الگوریتم SVM هستید یا در پیادهسازی آن به کمک نیاز دارید، همین حالا با DataYad تماس بگیرید و از مشاوره رایگان بهرهمند شوید! شماره تماس: [شماره تماس شما]
تحلیل دادههای پزشکی و تشخیص بیماریها با SVM
ماشین بردار پشتیبان در پزشکی برای تشخیص بیماریها مانند سرطان، دیابت یا بیماریهای قلبی بر اساس دادههای پزشکی (مانند تصاویر MRI، آزمایشهای خون یا سوابق بیماران) کاربرد دارد. این روش با دقت بالا به پزشکان در تشخیص دقیق و درمان بهتر کمک زیادی میکند.

مزایای SVM
– در مواردی که ابعاد دادهها بالاست، مؤثر است.
– حافظه کارآمد دارد زیرا از یک زیرمجموعه از نقاط آموزشی در تابع تصمیمگیری به نام بردارهای پشتیبان استفاده میکند.
– میتوان توابع کرنل مختلفی را برای توابع تصمیمگیری مشخص کرد و امکان مشخص کردن کرنلهای سفارشی وجود دارد.
معایب استفاده از SVM
به نقل از وبسایت geeksforgeeks.org:
“معایب ماشین بردار پشتیبان عبارتند از:
-
آموزش کند: SVM برای مجموعهدادههای بزرگ ممکن است کند عمل کند که این موضوع بر عملکرد آن در وظایف دادهکاوی تأثیر میگذارد.
-
دشواری تنظیم پارامترها: انتخاب کرنل مناسب و تنظیم پارامترهایی مانند C نیاز به دقت زیادی دارد و این موضوع میتواند بر عملکرد الگوریتمهای SVM تأثیر بگذارد.
-
حساسیت به نویز: SVM در مواجهه با دادههای نویزی یا کلاسهای همپوشان عملکرد ضعیفی دارد و این مسئله کارایی آن را در سناریوهای واقعی محدود میکند.
-
قابلیت تفسیر محدود: پیچیدگی هیپرپلین در ابعاد بالا باعث میشود SVM در مقایسه با مدلهای دیگر کمتر قابل تفسیر باشد.
-
حساسیت به مقیاسدهی ویژگیها: مقیاسدهی مناسب ویژگیها ضروری است؛ در غیر این صورت، مدلهای SVM ممکن است عملکرد ضعیفی داشته باشند.”

محدودیتهای SVM
ماشین بردار پشتیبان با وجود مزایای زیاد محدودیتهایی نیز دارد. این الگوریتم در مواجهه با دیتاستهای بزرگ و نویزی عملکرد ضعیفی دارد، زیرا زمان آموزش مدل بهطور قابل توجهی افزایش مییابد و حساسیت به نویز میتواند منجر به بیشبرازش (Overfitting) شود. همچنین تنظیم پارامترهای SVM مانند انتخاب کرنل مناسب و مقدار C نیاز به دقت زیادی دارد و ممکن است فرآیندی زمانبر باشد. علاوه بر این تفسیر مدلهای SVM در ابعاد بالا دشوار است و برای عملکرد بهتر، نیاز به مقیاسدهی دقیق ویژگیها دارد. این محدودیتها باعث میشوند SVM در برخی سناریوهای واقعی کمتر مؤثر باشد.
عملکرد ضعیف در دیتاستهای بزرگ و نویزی
ماشین بردار پشتیبان در مواجهه با دیتاستهای بزرگ و نویزی با چالشهایی همراه است. در دیتاستهای بزرگ، زمان آموزش مدل بهطور قابل توجهی افزایش مییابد، زیرا SVM نیاز به محاسبات پیچیدهای برای یافتن هیپرپلین بهینه دارد. همچنین در دیتاستهای نویزی یا دادههایی که کلاسها همپوشانی زیادی دارند، SVM ممکن است عملکرد ضعیفی از خود نشان دهد، زیرا این الگوریتم سعی میکند حاشیهی بیشینه را حفظ کند و این موضوع میتواند منجر به بیشبرازش (Overfitting) یا کاهش دقت مدل شود. این محدودیتها باعث میشوند SVM در برخی سناریوهای واقعی، مانند دادههای دارای نویز یا حجم بسیار بالا، اثر کمتری داشته باشد.
پیادهسازی SVM در پایتون
پیشبینی اینکه آیا سرطان خوشخیم است یا بدخیم. استفاده از دادههای تاریخی در مورد بیمارانی که با تشخیص سرطان مواجه شدهاند، به پزشکان این امکان را میدهد که موارد بدخیم و خوشخیم را با توجه به ویژگیهای مستقل تفکیک کنند.
مراحل:
1. بارگذاری مجموعه داده سرطان سینه از sklearn.datasets
2. جداسازی ویژگیهای ورودی و متغیرهای هدف.
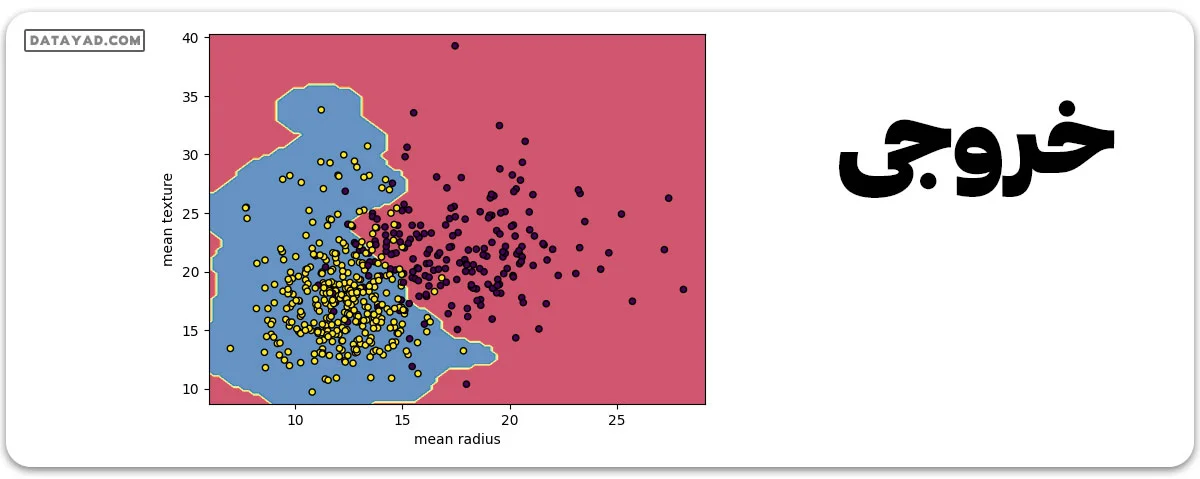
3. ساخت و آموزش طبقهبندهای SVM با استفاده از کرنل RBF.
4. رسم نمودار پراکندگی ویژگیهای ورودی.
5. رسم مرز تصمیمگیری.
6. رسم مرز تصمیمگیری.
# Load the important packages from sklearn.datasets import load_breast_cancer import matplotlib.pyplot as plt from sklearn.inspection import DecisionBoundaryDisplay from sklearn.svm import SVC # Load the datasets cancer = load_breast_cancer() X = cancer.data[:, :2] y = cancer.target #Build the model svm = SVC(kernel="rbf", gamma=0.5, C=1.0) # Trained the model svm.fit(X, y) # Plot Decision Boundary DecisionBoundaryDisplay.from_estimator( svm, X, response_method="predict", cmap=plt.cm.Spectral, alpha=0.8, xlabel=cancer.feature_names[0], ylabel=cancer.feature_names[1], ) # Scatter plot plt.scatter(X[:, 0], X[:, 1], c=y, s=20, edgecolors="k") plt.show()
مقایسه ماشین بردار پشتیبان با سایر الگوریتمهای طبقهبندی
ماشین بردار پشتیبان یکی از الگوریتمهای قدرتمند در حوزهی یادگیری نظارتشده است که در مقایسه با سایر روشهای طبقهبندی مانند درخت تصمیم، رگرسیون لجستیک و شبکههای عصبی مزایا و معایب خاص خود را دارد. SVM در دادههای با ابعاد بالا و مسائل غیرخطی (با استفاده از کرنلهای مناسب) عملکرد بسیار خوبی داشته و با تمرکز بر بیشینهکردن حاشیهی تصمیمگیری، تعمیمپذیری بالایی دارد. با این حال در مقایسه با درخت تصمیم، تفسیرپذیری کمتری دارد و در مقایسه با شبکههای عصبی، برای دیتاستهای بسیار بزرگ و پیچیده ممکن است کندتر عمل کند. همچنین برخلاف رگرسیون لجستیک که برای دادههای خطی سادهتر است، SVM نیاز به تنظیم دقیق پارامترها دارد.
مقایسه SVM با KNN
ماشین بردار پشتیبان و الگوریتم K-نزدیکترین همسایه (KNN) هر دو از روشهای پرکاربرد در یادگیری نظارتشده هستند، اما تفاوتهای اساسی با هم دارند. SVM با ایجاد یک مرز تصمیمگیری بهینه (هیپرپلین) و بیشینهکردن حاشیه بین کلاسها، عملکرد قویای در دادههای با ابعاد بالا و مسائل غیرخطی (با استفاده از کرنلها) دارد. در مقابل، KNN با محاسبه فاصلهی نقاط داده از همسایههای نزدیک، یک روش ساده و مبتنی بر نمونه است که نیازی به آموزش مدل ندارد. اغلب KNN در دادههای با ابعاد بالا دچار مشکل “مصرف محاسباتی زیاد” میشود، در حالی که SVM در این موارد عملکرد بهتری دارد. از سوی دیگر KNN به نویز حساس است، در حالی که SVM با تنظیم پارامتر C میتواند نویز را بهتر مدیریت کند. در کل SVM برای دادههای پیچیده و بزرگ مناسبتر است، در حالی که KNN برای دادههای کوچک و سادهتر کارایی بهتری دارد.
دقت و عملکرد در دادههای پر نویز
در مواجهه با دادههای پر نویز، ماشین بردار پشتیبان و KNN رفتار متفاوتی از خود نشان میدهند. SVM با استفاده از پارامتر تنظیمکنندهی C، میتواند نویز را تا حدی مدیریت کرده و با ایجاد یک حاشیهی نرم (Soft Margin)، از تأثیر نقاط نویزی بر مدل جلوگیری کند. این ویژگی باعث میشود SVM در دادههای پر نویز عملکرد بهتری داشته باشد. از سوی دیگر KNN به دلیل ماهیت مبتنی بر همسایهها، به شدت تحت تأثیر نویز قرار میگیرد، زیرا نقاط نویزی میتوانند بر تصمیمگیری مدل تأثیر منفی بگذارند و دقت آن را کاهش دهند. بنابراین، در دادههای پر نویز، معمولاً SVM گزینهی بهتری نسبت به KNN است.
سرعت پردازش و پیچیدگی محاسباتی
سرعت پردازش و پیچیدگی محاسباتی در ماشین بردار پشتیبان و KNN تفاوتهای قابل توجهی دارد. SVM در مرحلهی آموزش، نیاز به حل یک مسئلهی بهینهسازی پیچیده دارد که میتواند برای دیتاستهای بزرگ زمانبر باشد، اما پس از آموزش، پیشبینیها سریع انجام میشود. از طرف دیگر KNN نیازی به مرحلهی آموزش ندارد و مدل بلافاصله آمادهی استفاده است، اما در مرحلهی پیشبینی، باید فاصلهی هر نقطهی جدید را با تمام نقاط آموزشی محاسبه کند. این موضوع برای دیتاستهای بزرگ یا با ابعاد بالا میتواند بسیار کند و پرهزینه باشد. بنابراین، SVM برای دادههای بزرگ و پیچیده مناسبتر است، در حالی که KNN برای دادههای کوچک و سادهتر کارایی بهتری دارد.
مقایسه SVM با درخت تصمیم (Decision Tree)
ماشین بردار پشتیبان و درخت تصمیم (Decision Tree) هر دو از الگوریتمهای پرکاربرد در یادگیری نظارتشده هستند، اما تفاوتهای مهمی با یکدیگر دارند. SVM با ایجاد یک مرز تصمیمگیری بهینه (هیپرپلین) و بیشینهکردن حاشیه بین کلاسها، عملکرد قویای در دادههای با ابعاد بالا و مسائل غیرخطی (با استفاده از کرنلها) دارد. برخلاف SVM، درخت تصمیم با تقسیمبندی دادهها بر اساس ویژگیها، ساختاری شبیه به درخت ایجاد میکند که تفسیرپذیری بالایی دارد. با این حال درختهای تصمیم بهراحتی میتوانند دچار بیشبرازش (Overfitting) شوند، در حالی که SVM با تنظیم پارامتر C میتواند این مسئله را بهتر مدیریت کند.

قابلیت تعمیم (Generalization) و Overfitting
ماشین بردار پشتیبان و درخت تصمیم در قابلیت تعمیم (Generalization) و مدیریت بیشبرازش (Overfitting) رفتار متفاوتی دارند. SVM با تمرکز بر بیشینهکردن حاشیهی تصمیمگیری، تمایل به ایجاد مدلهایی با قابلیت تعمیم بالا دارد، بهویژه زمانی که از کرنلهای مناسب و پارامتر C بهدرستی تنظیم شده استفاده شود. این ویژگی باعث میشود SVM در برابر بیشبرازش مقاومتر باشد. از طرف دیگر درخت تصمیم بهراحتی میتواند دچار بیشبرازش شود، زیرا ممکن است تا حد زیادی به دادههای آموزشی وابسته شود و ساختار پیچیدهای ایجاد کند. معمولاً برای جلوگیری از این مشکل، از روشهایی مانند هرس درخت (Pruning) یا استفاده از جنگلهای تصادفی (Random Forest) کمک گرفته میشود.
پیچیدگی محاسباتی و زمان آموزش مدل
ماشین بردار پشتیبان و درخت تصمیم از نظر پیچیدگی محاسباتی و زمان آموزش مدل تفاوتهای قابل توجهی دارند. SVM نیاز به حل یک مسئلهی بهینهسازی پیچیده دارد که میتواند برای دیتاستهای بزرگ زمانبر باشد، به خصوص زمانی که از کرنلهای غیرخطی مانند RBF استفاده میشود. در مقابل درخت تصمیم اغلب سریعتر آموزش میبیند، زیرا ساختار درخت با تقسیمبندی سادهی دادهها ایجاد میشود. اما در دادههای با ابعاد بالا یا پیچیده، ممکن است زمان آموزش افزایش یابد. در واقع SVM برای دادههای پیچیده و بزرگ مناسبتر است، در حالی که درخت تصمیم برای دادههای کوچکتر و سادهتر، گزینهی سریعتر و کارآمدتری شناخته میشود.
مقایسه SVM با شبکههای عصبی (Neural Networks)
ماشین بردار پشتیبان و شبکههای عصبی هر دو از الگوریتمهای قدرتمند در یادگیری ماشین هستند، اما تفاوتهای اساسی دارند. SVM با ایجاد یک مرز تصمیمگیری بهینه (هیپرپلین) و بیشینهکردن حاشیه بین کلاسها، عملکرد قویای در دادههای با ابعاد بالا و مسائل غیرخطی (با استفاده از کرنلها) دارد. این روش به دادههای کمتر ولی با کیفیت بالا وابسته است و معمولاً نیاز به تنظیم دقیق پارامترها دارد. در مقابل شبکههای عصبی با ساختار لایهای و توانایی یادگیری ویژگیهای پیچیده، برای دادههای بسیار بزرگ و مسائل با ساختار پیچیده (مانند تصاویر و متن) مناسبتر هستند. با این حال شبکههای عصبی نیاز به دادههای آموزشی زیاد و محاسبات سنگینتری دارند و تفسیرپذیری کمتری نسبت به SVM ارائه میدهند.
عملکرد در دادههای پیچیده و غیرخطی
ماشین بردار پشتیبان با استفاده از توابع کرنل (مانند RBF یا چندجملهای) میتواند دادههای پیچیده و غیرخطی را بهطور مؤثر جدا کند. این الگوریتم با نگاشت دادهها به فضایی با ابعاد بالاتر، مرزهای تصمیمگیری پیچیده را ایجاد میکند و برای مسائلی که نیاز به دقت بالا دارند، مناسب است. شبکههای عصبی بهطور ذاتی توانایی یادگیری ویژگیهای پیچیده و غیرخطی را دارند و با ساختار لایهای خود، میتوانند الگوهای پیچیدهتری را نسبت به SVM تشخیص دهند. این ویژگی باعث میشود شبکههای عصبی در مسائلی مانند پردازش تصویر و زبان طبیعی عملکرد بهتری داشته باشند.
هزینه محاسباتی و نیاز به دادههای بزرگ
ماشین بردار پشتیبان برای دادههای کوچک تا متوسط بسیار مؤثر است، اما در دیتاستهای بزرگ، هزینه محاسباتی آن بهطور قابل توجهی افزایش مییابد، زیرا نیاز به حل یک مسئله بهینهسازی پیچیده دارد. شبکههای عصبی برای عملکرد بهینه به حجم زیادی از دادههای آموزشی نیاز دارند و آموزش آنها میتواند بسیار زمانبر و پرهزینه باشد. توجه داشته باشید که شبکههای عصبی با استفاده از سختافزارهای پیشرفته (مانند GPU) میتوانند این چالش را تا حدی مدیریت کنند.
نکات پیشرفته و بهینهسازی مدل SVM
برای بهینهسازی مدل ماشین بردار پشتیبان، انتخاب کرنل مناسب (مانند RBF یا چندجملهای) و تنظیم دقیق پارامترهایی مانند C (تنظیمکنندهی حاشیه) و گاما (در کرنل RBF) اهمیت زیادی دارد. استفاده از تکنیکهایی مانند جستجوی شبکهای (Grid Search) یا جستجوی تصادفی (Random Search) برای یافتن بهترین ترکیب پارامترها توصیه میشود. همچنین مقیاسدهی ویژگیها و کاهش ابعاد دادهها میتواند عملکرد مدل را بهبود ببخشد. حال اگر به دنبال یادگیری عمیقتر الگوریتم SVM هستید یا در پیادهسازی آن به کمک نیاز دارید، همین حالا با DataYad تماس بگیرید و از مشاوره رایگان بهرهمند شوید! شماره تماس: [شماره تماس شما]
لیست دروس دوره
- درس 1: شروع کار با یادگیری ماشین
- درس 2: یادگیری ماشین چیست؟
- درس 3: انواع یادگیری ماشین، چالش ها و کاربردهای آن
- درس 4: معرفی داده در یادگیری ماشین
- درس 5: بهترین کتابخانه های پایتون برای یادگیری ماشین
- درس 6: جذاب ترین کاربردهای یادگیری ماشین
- درس 7: تفاوت های یادگیری ماشین و هوش مصنوعی
- درس 8: درک پردازش داده (Data Processing)
- درس 9: تولید دادههای تست برای یادگیری ماشین
- درس 10: پیش پردازش داده ها در پایتون
- درس 11: پاکسازی داده ها و مراحل آن
- درس 12: کدگذاری برچسب با پایتون
- درس 13: روش کدبندی وان هات (One Hot Encoding)
- درس 14: مقابله با دادههای نامتوازن
- درس 15: یادگیری ماشین تحت نظارت
- درس 16: طبقه بندی (Classification)
- درس 17: انواع تکنیک های رگرسیون
- درس 18: تفاوت الگوریتم های طبقه بندی و رگرسیون
- درس 19: رگرسیون خطی
- درس 20: پیاده سازی رگرسیون خطی در پایتون
- درس 21: رگرسیون خطی تک متغیره در پایتون
- درس 22: رگرسیون خطی چندگانه در پایتون
- درس 23: رگرسیون خطی با کتابخانه sklearn
- درس 24: رگرسیون خطی با استفاده از تنسورفلو (TensorFlow)
- درس 25: رگرسیون خطی با استفاده از PyTorch
- درس 26: Pyspark – رگرسیون خطی با استفاده از آپاچی MLlib
- درس 27: چالش دیتاست مسکن بوستون با استفاده از رگرسیون خطی
- درس 28: پیادهسازی رگرسیون چندجمله ای با پایتون از پایه
- درس 29: پیاده سازی رگرسیون چندجمله ای با پایتون
- درس 30: رگرسیون چندجملهای برای داده های غیرخطی
- درس 31: پیاده سازی رگرسیون چندجمله ای با Turicreate
- درس 32: رگرسیون لجستیک در یادگیری ماشین
- درس 33: رگرسیون لجستیک با استفاده از پایتون
- درس 34: رگرسیون لجستیک با استفاده از tensorflow
- درس 35: رگرسیون سافت مکس (Softmax) با استفاده از Tensorflow
- درس 36: رگرسیون Softmax با استفاده از Keras
- درس 37: دسته بندی کننده های بیز ساده (Naive Bayes)
- درس 38: پیادهسازی بیز ساده (Naive Bayes) با استفاده از پایتون
- درس 39: الگوریتم مکمل بیز ساده (CNB)
- درس 40: کاربرد بیز ساده چند جملهای در NLP
- درس 41:الگوریتم ماشین بردار پشتیبان (SVM)
- درس 42: دستهبندی دادهها با استفاده از SVMها در پایتون
- درس 43: تنظیم پارامترهای SVM با استفاده از GridSearchCV
- درس 44: ایجاد SVM با کرنل خطی در پایتون
- درس 45: توابع کرنل اصلی در SVM
- درس ۴۶: استفاده از SVM برای دستهبندی در یک مجموعه داده غیرخطی
- درس 47: درخت تصمیم (Decision Tree) چیست؟
- درس 48: پیادهسازی درخت تصمیم با پایتون
- درس 49: استفاده از رگرسیون درخت تصمیم با استفاده از sklearn
- درس 50: رگرسیون جنگل تصادفی در پایتون
- درس 51: ساخت طبقهبندیکننده جنگل تصادفی با کتابخانه Scikit-Learn
آموزش پیشنهادی و مکمل
دوره جامع متخصص علم داده (یادگیری ماشین، یادگیری عمیق)

سوالات متداول
1-چگونه از ماشین بردار پشتیبان در پروژههای خود استفاده کنیم؟
برای استفاده از SVM، ابتدا دادههای خود را آماده کنید (مقیاسدهی و پیشپردازش). سپس با استفاده از کتابخانههایی مانند Scikit-learn، مدل SVM را پیادهسازی کرده و با تنظیم پارامترهای مناسب، آن را آموزش دهید. در نهایت، مدل را ارزیابی و بهبود ببخشید.
2-بهترین روشها برای تنظیم پارامترهای SVM چیست؟
از جستجوی شبکهای (Grid Search) یا جستجوی تصادفی (Random Search) برای یافتن بهترین مقادیر پارامترهای C، گاما و نوع کرنل استفاده کنید. همچنین اعتبارسنجی متقابل (Cross-Validation) میتواند به بهبود عملکرد مدل کمک کند.
3-SVM بهتر است یا شبکههای عصبی؟
SVM برای دادههای کوچک تا متوسط و نیازمند دقت بالا مناسب است، در حالی که شبکههای عصبی برای دادههای بزرگ و پیچیده (مانند تصاویر و متن) عملکرد بهتری دارند. انتخاب بین این دو به ماهیت دادهها و نیازهای پروژه بستگی دارد.