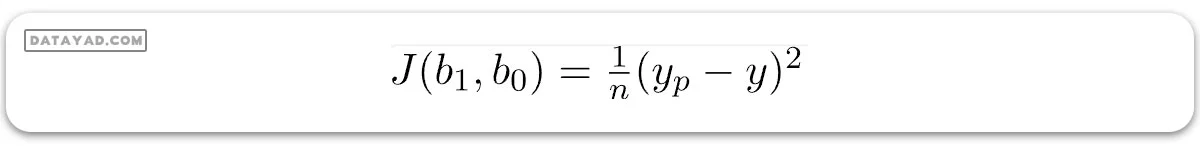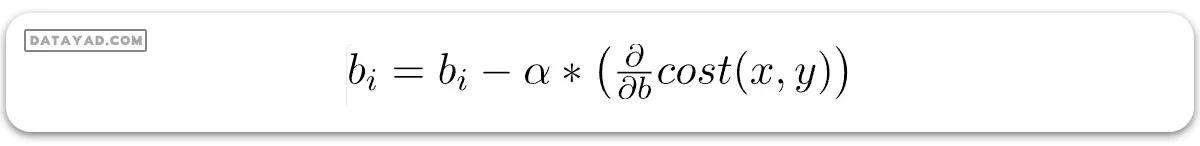در این مقاله، به توضیح رگرسیون خطی تک متغیره می‌پردازیم. این نوع رگرسیون، از ساده‌ترین انواع رگرسیون‌ها است. در این روش، ما مقدار مورد نظرمان را فقط با استفاده از یک متغیر مستقل پیش‌بینی می‌کنیم.
رگرسیون خطی تک متغیره در پایتون
رگرسیون خطی تک متغیره (Univariate Linear Regression) نوعی رگرسیون است که در آن، متغیر مورد نظر فقط به یک متغیر مستقل وابسته است. در این نوع رگرسیون، داده‌هایی که استفاده می‌شوند تک متغیره هستند.
برای مثال، می‌توان یک مجموعه داده شامل نقاط روی خط را در نظر گرفت که در آن، مقادیر روی محور افقی به عنوان ورودی و مقادیر روی محور عمودی به عنوان خروجی یا هدف تلقی می‌شوند.
مثالی از رگرسیون خطی تک متغیره
برای خط Y = 2X + 3؛ ویژگی ورودی X خواهد بود و Y هدف قرار می‌گیرد.
مفهوم: در رگرسیون خطی تک متغیره، فقط یک بردار ویژگی ورودی وجود دارد. خط رگرسیون به شکل زیر خواهد بود:
Y = b0 + b1 * X
که در آن، b0 و b1 ضرایب رگرسیون هستند.
در اینجا ما سعی می‌کنیم بهترین b0 و b1 را با آموزش یک مدل پیدا کنیم تا متغیر پیش‌بینی شده y ما کمترین اختلاف را با y واقعی داشته باشد.
یک مدل رگرسیون خطی تک متغیره شامل چندین تابع کاربردی است. ما هر تابع را یک به یک تعریف می‌کنیم و در پایان، آن‌ها را در یک کلاس ترکیب می‌کنیم تا یک مدل کاربردی رگرسیون خطی تک‌متغیره به وجود آید.
توابع کاربردی در مدل رگرسیون خطی تک متغیره
- پیش‌بینی با رگرسیون خطی
- تابع هزینه
- گرادیان کاهشی برای تخمین پارامترها
- به‌روزرسانی ضرایب
- توقف تکرارها
پیش‌بینی با رگرسیون خطی
در این تابع، ما با ضرب کردن و اضافه کردن ضریب رگرسیون به x، مقدار y را بر اساس مقدار داده‌شده x پیش‌بینی می‌کنیم.
# Y = b0 + b1 * X def predict(x, b0, b1): return b0 + b1 * x
تابع هزینه برای رگرسیون خطی تک متغیره
تابع هزینه، خطا را با مقادیر فعلی ضرایب رگرسیون محاسبه می‌کند. این تابع به صورت کمّی تعریف می‌کند که چقدر مقدار پیش‌بینی شده توسط مدل از مقدار واقعی با توجه به ضرایب رگرسیون که کمترین نرخ خطا را دارند، فاصله دارد.
خطای میانگین مربعات (MSE) = مجموع مربعات اختلاف بین مقادیر پیش‌بینی شده و واقعی
ما از مربع استفاده می‌کنیم تا خطای مثبت و منفی یکدیگر را خنثی نکنند.
در اینجا:
- y فهرستی از مقادیر مورد انتظار است
- x متغیر مستقل است
- b0 و b1 ضرایب رگرسیون هستند
def cost(x, y, b0, b1): errors = [] for x, y in zip(x, y): prediction = predict(x, b0, b1) expected = y difference = prediction-expected errors.append(difference) mse = sum([error * error for error in errors])/len(errors) return mse
گرادیان کاهشی برای برآورد پارامترها
ما از روش گرادیان کاهشی (Gradient descent) برای به‌روز کردن ضرایب رگرسیون استفاده خواهیم کرد. این یک الگوریتم بهینه‌سازی است که برای آموزش مدلمان به کار می‌بریم. در گرادیان کاهشی، مشتق جزئی تابع هزینه را نسبت به ضرایب رگرسیون می‌گیریم، با نرخ یادگیری آلفا ضرب می‌کنیم و از ضرایبمان کم می‌کنیم تا ضرایب رگرسیون مان را تعدیل کنیم.
برای ساده‌سازی، ما کاهش گرادیان را تنها روی یک عنصر از داده‌ها اعمال می‌کنیم و سعی می‌کنیم بر اساس این روش، ضرایب رگرسیون خطی تک‌متغیره‌مان را برآورد کنیم.
چون تابع هزینه ما دو پارامتر b1 و b دارد، ابتدا مشتق تابع هزینه را نسبت به b1 و سپس نسبت به b می‌گیریم.
تابع پایتون برای گرادیان کاهشی
def grad_fun(x, y, b0, b1, i): return sum([ 2*(predict(xi, b0, b1)-yi)*1 if i == 0 else 2*(predict(xi, b0, b1)-yi)*xi for xi, yi in zip(x, y) ])/len(x)
به‌روزرسانی ضرایب در رگرسیون خطی تک متغیره
در هر دور تکرار (epoch)، مقادیر ضرایب رگرسیون بر اساس خطای دوره قبلی و با یک مقدار مشخص به‌روز می‌شوند. این به‌روزرسانی بخش مهمی از برنامه‌های یادگیری ماشین است که می‌نویسید.
به‌روز کردن ضرایب با کاستن از مقدار آن‌ها به اندازه بخشی از خطایی که قبلاً ایجاد کرده‌اند انجام می‌شود. این بخش، نرخ یادگیری نامیده می‌شود و تعیین می‌کند که مدل ما چقدر سریع به نقطه همگرایی (جایی که خطا ایده‌آل است و به صفر می‌رسد) می‌رسد.
def update_coeff(x, y, b0, b1, i, alpha): bi -= alpha * cost_derivative(x, y, b0, b1, i) return bi
توقف تکرارها
این تابع برای تعیین زمان پایان تکرارها استفاده می‌شود. بر اساس تنظیمات کاربر، تابع توقف تکرارها معمولاً در شرایط زیر فعال می‌شود:
- حداکثر تعداد تکرار: زمانی که مدل به تعداد معینی از تکرارها آموزش دیده باشد.
- مقدار خطا: اگر خطای قبلی کمتر یا برابر با یک سطح مشخص باشد، الگوریتم می‌تواند توقف کند.
- دقت: اگر دقت آخرین مدل از میزان مشخص‌شده بیشتر باشد، الگوریتم توقف می‌کند.
- روش ترکیبی: این روش که اغلب استفاده می‌شود، ترکیبی از چند شرط فوق است و همچنین شامل یک گزینه وقفه اضطراری است. وقفه اضطراری در شرایطی رخ می‌دهد که اتفاق ناخواسته‌ای مانند بیش‌فراز شدن نتایج یا تجاوز از محدودیت‌های زمانی اتفاق بیفتد.
پس از تعریف تمام توابع کاربردی، بیایید نگاهی به شبه‌کد (Pseudocode) بیندازیم و سپس به پیاده‌سازی آن بپردازیم:
Pseudocode برای رگرسیون خطی
x, y is the given data.
(b0, b1) <-- (0, 0)
i = 0
while True:
if stop_iteration(i):
break
else:
b0 = update_coeff(x, y, b0, b1, 0, alpha)
b1 = update_coeff(x, y, b0, b1, 1, alpha)
پیاده‌سازی کامل رگرسیون خطی تک متغیره با استفاده از پایتون
class LinearRegressor:
def __init__(self, x, y, alpha=0.01, b0=0, b1=0):
"""
x: input feature
y: result / target
alpha: learning rate, default is 0.01
b0, b1: linear regression coefficient.
"""
self.i = 0
self.x = x
self.y = y
self.alpha = alpha
self.b0 = b0
self.b1 = b1
if len(x) != len(y):
raise TypeError("""x and y should have same number of rows.""")
def predict(model, x):
"""Predicts the value of prediction based on
current value of regression coefficients
when input is x"""
return model.b0 + model.b1 * x
def grad_fun(model, i):
x, y, b0, b1 = model.x, model.y, model.b0, model.b1
predict = model.predict
return sum([
2 * (predict(xi) - yi) * 1
if i == 0
else (predict(xi) - yi) * xi
for xi, yi in zip(x, y)
]) / len(x)
def update_coeff(model, i):
cost_derivative = model.cost_derivative
if i == 0:
model.b0 -= model.alpha * cost_derivative(i)
elif i == 1:
model.b1 -= model.alpha * cost_derivative(i)
def stop_iteration(model, max_epochs=1000):
model.i += 1
if model.i == max_epochs:
return True
else:
return False
def fit(model):
update_coeff = model.update_coeff
model.i = 0
while True:
if model.stop_iteration():
break
else:
update_coeff(0)
update_coeff(1)
شروع با مقداردهی اولیه به مدل
linearRegressor = LinearRegressor( x=[i for i in range(12)], y=[2 * i + 3 for i in range(12)], alpha=0.03 ) linearRegressor.fit() print(linearRegressor.predict(12))
خروجی:
27.00000004287766
