پیاده سازی رگرسیون خطی در پایتون

این مقاله به بررسی اصول اولیه رگرسیون خطی و پیاده سازی رگرسیون خطی در پایتون می‌پردازد. رگرسیون خطی یک روش آماری است برای مدل‌سازی روابط بین یک متغیر وابسته با مجموعه‌ای از متغیرهای مستقل که در درس نوزدهم آموزش رایگان یادگیری ماشین با پایتون در مورد آن کامل صحبت کردیم.

توجه: در این مقاله، به منظور سادگی، به متغیرهای وابسته به عنوان پاسخ‌ها و به متغیرهای مستقل به عنوان ویژگی‌ها اشاره می‌کنیم. برای فراهم کردن درک پایه‌ای از رگرسیون خطی، با ساده‌ترین نوع رگرسیون خطی، یعنی رگرسیون خطی ساده، شروع می‌کنیم.

رگرسیون خطی ساده

رگرسیون خطی ساده یک روش برای پیش‌بینی یک پاسخ با استفاده از یک ویژگی منفرد است. این مدل یکی از ابتدایی‌ترین مدل‌هایی است که علاقه‌مندان به یادگیری ماشین با آن آشنا می‌شوند.

در رگرسیون خطی، ما بر این فرض هستیم که دو متغیر وابسته و مستقل با هم رابطه‌ای خطی دارند. از این رو، تلاش می‌کنیم تا تابع خطی‌ای بیابیم که بتواند مقدار پاسخ (y) را بر اساس ویژگی یا متغیر مستقل (x) با بالاترین دقت ممکن پیش‌بینی کند. فرض کنید مجموعه داده‌ای داریم که در آن برای هر ویژگی (x)، مقدار پاسخ (y) را داریم.

برای عمومیت بیشتر، ما تعریف می‌کنیم:

x را به عنوان بردار ویژگی، یعنی (x = [x_1, x_2, …., x_n]),

y را به عنوان بردار پاسخ، یعنی (y = [y_1, y_2, …., y_n])

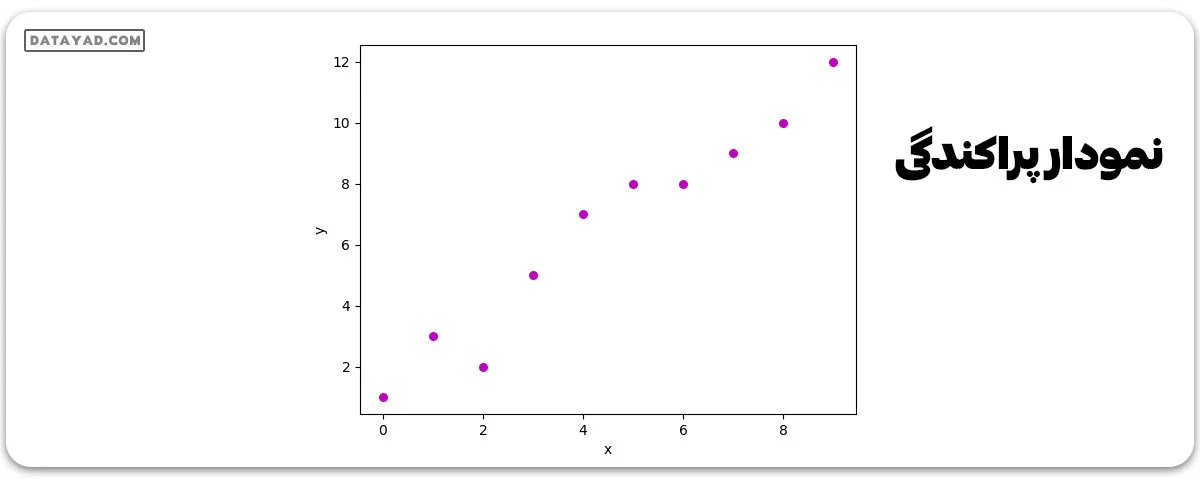
برای n مشاهدات (در مثال بالا، ( n=10)). نمودار پراکندگی این مجموعه داده به این شکل است:

حالا، وظیفه ما این است که یک خط پیدا کنیم که به بهترین شکل روی نمودار پراکندگی بالا قرار گیرد تا بتوانیم برای هر مقدار جدید ویژگی‌ها، پاسخ را پیش‌بینی کنیم (یعنی مقداری از x که در مجموعه داده‌ها حضور ندارد). این خط را خط رگرسیون می‌نامند. معادله خط رگرسیون به این شکل نمایش داده می‌شود:

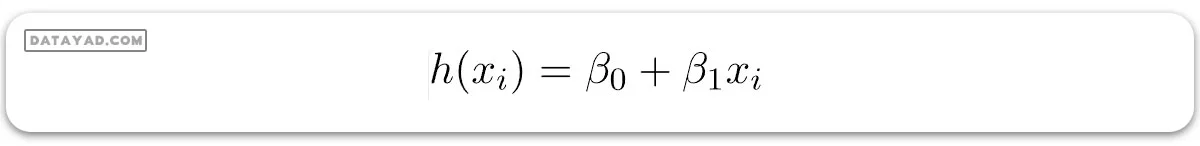
در اینجا:

• h(x_i) مقدار پاسخ پیش‌بینی شده برای مشاهده i ام را نشان می‌دهد.
• (ß) و (ß₁) ضرایب رگرسیون هستند و به ترتیب نمایانگر برش با محور y و شیب خط رگرسیون می‌باشند.

برای ایجاد مدل ما، باید مقادیر ضرایب رگرسیون ß و ß₁ را یاد بگیریم یا برآورد کنیم. پس از برآورد این ضرایب، می‌توانیم از مدل برای پیش‌بینی پاسخ‌ها استفاده نماییم. در این مقاله، ما از اصل کمینه‌سازی حداقل مربعات خطاها استفاده خواهیم کرد.

حال فرض کنید:

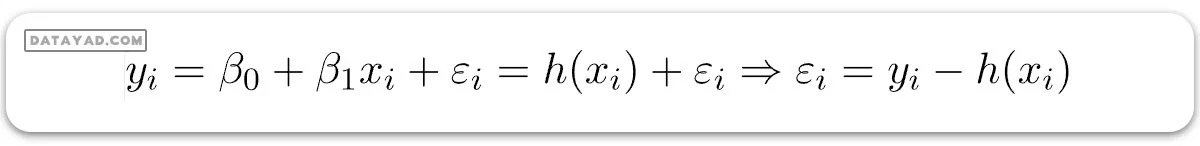
در اینجا (ε_i) خطای باقی‌مانده در مشاهده i ام است. پس هدف ما کمینه کردن مجموع خطاهای باقی‌مانده است. ما تابع خطای مربعی یا تابع هزینه، J را به صورت زیر تعریف می‌کنیم:

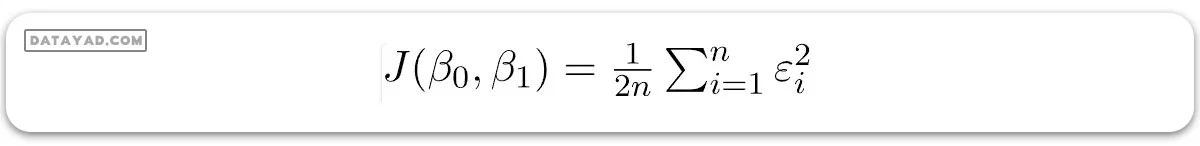
و وظیفه ما یافتن مقادیر (ß) و (ß₁) است به طوری که (ß_{0 ,} ß₁)J کمینه شود. بدون ورود به جزئیات ریاضی، نتیجه را در اینجا ارائه می‌دهیم:

جایی که SSxy مجموع انحرافات متقابل y و x است:

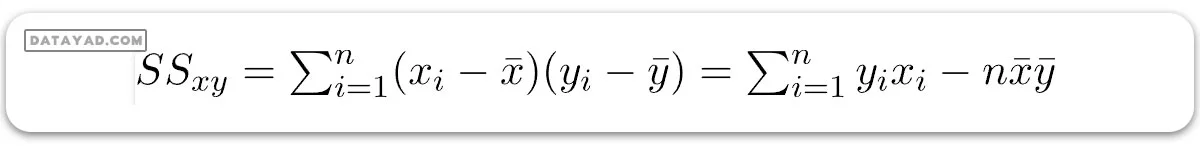
و SSxx مجموع انحرافات مربعی x است:

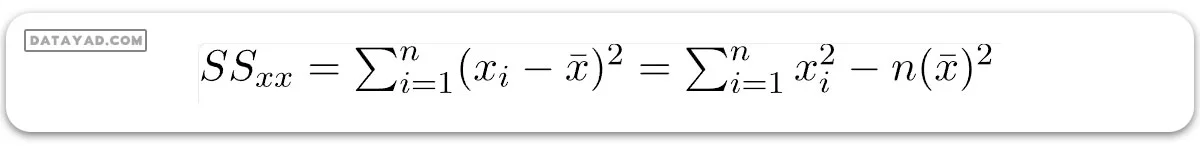
پیاده سازی رگرسیون خطی در پایتون

ما می‌توانیم از زبان برنامه‌ نویسی پایتون برای یادگیری ضرایب مدل‌های رگرسیون خطی استفاده کنیم. برای رسم داده‌های ورودی و بهترین خط برازش، از کتابخانه matplotlib استفاده خواهیم کرد. این کتابخانه یکی از پرکاربردترین کتابخانه‌ های پایتون برای رسم نمودارها است.

import numpy as np
import matplotlib.pyplot as plt

def estimate_coef(x, y):
	# number of observations/points
	n = np.size(x)

	# mean of x and y vector
	m_x = np.mean(x)
	m_y = np.mean(y)

	# calculating cross-deviation and deviation about x
	SS_xy = np.sum(y*x) - n*m_y*m_x
	SS_xx = np.sum(x*x) - n*m_x*m_x

	# calculating regression coefficients
	b_1 = SS_xy / SS_xx
	b_0 = m_y - b_1*m_x

	return (b_0, b_1)

def plot_regression_line(x, y, b):
	# plotting the actual points as scatter plot
	plt.scatter(x, y, color = "m",
			marker = "o", s = 30)

	# predicted response vector
	y_pred = b[0] + b[1]*x

	# plotting the regression line
	plt.plot(x, y_pred, color = "g")

	# putting labels
	plt.xlabel('x')
	plt.ylabel('y')

	# function to show plot
	plt.show()

def main():
	# observations / data
	x = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
	y = np.array([1, 3, 2, 5, 7, 8, 8, 9, 10, 12])

	# estimating coefficients
	b = estimate_coef(x, y)
	print("Estimated coefficients:\nb_0 = {} \
		\nb_1 = {}".format(b[0], b[1]))

	# plotting regression line
	plot_regression_line(x, y, b)

if __name__ == "__main__":
	main()

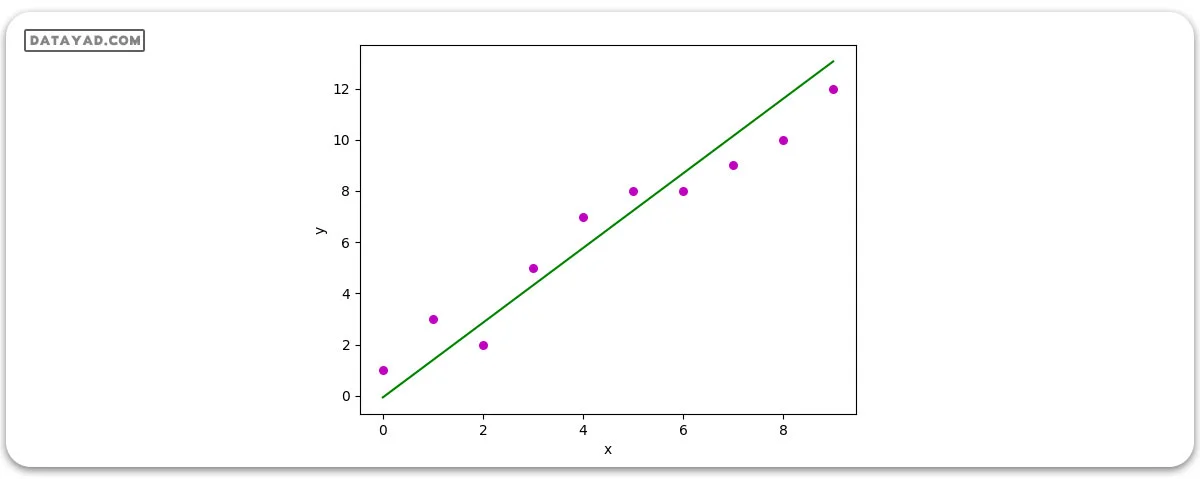
 خروجی:

Estimated coefficients:
b_0 = -0.0586206896552
b_1 = 1.45747126437

و نمودار حاصل به این شکل است:

رگرسیون خطی چندگانه (Multiple Linear Regression)

رگرسیون خطی چندگانه یا چند متغیره (MLR) تلاش می‌کند تا رابطه بین دو یا چند ویژگی و یک پاسخ را با قرار دادن یک معادله خطی روی داده‌های مشاهده شده، مدل‌سازی کند.

این روش در واقع گسترش یافته‌ای از رگرسیون خطی ساده است. فرض کنید مجموعه داده‌ای داریم که شامل p ویژگی (یا متغیرهای مستقل) و یک پاسخ (یا متغیر وابسته) است.

همچنین، مجموعه داده‌ها شامل n ردیف/مشاهدات است.

تعریف می‌کنیم:

X (ماتریس ویژگی‌ها) = یک ماتریس با اندازه n X p  که در آن x_ij مقادیر ویژگی j ام را برای مشاهده i ام نشان می‌دهد.

بنابراین:

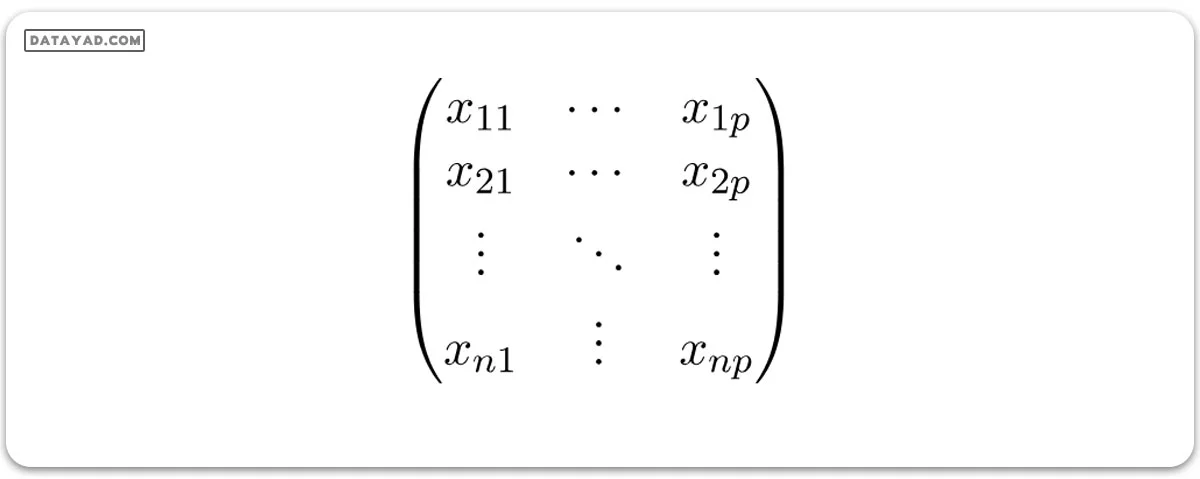
و:

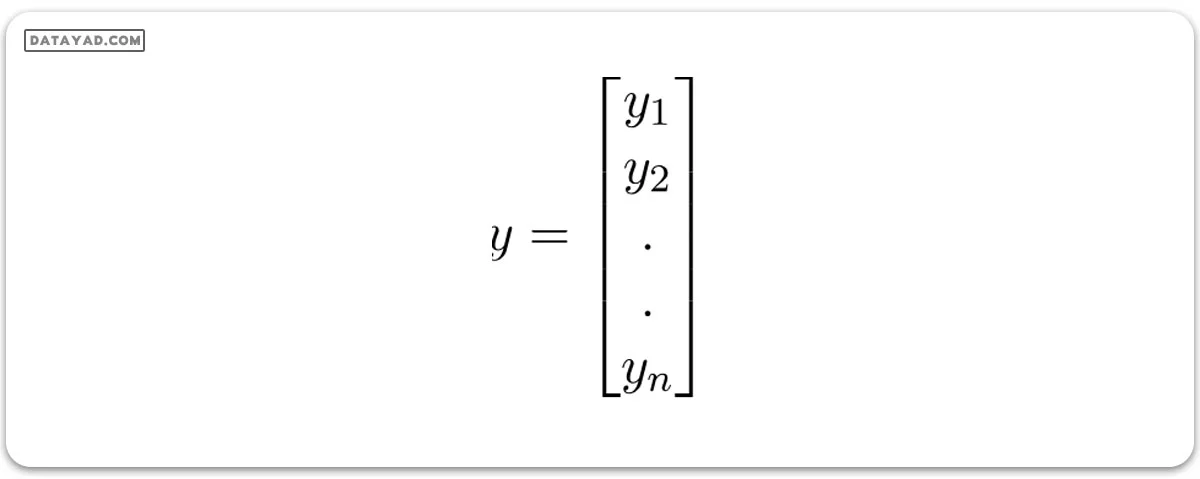
y (بردار پاسخ) = برداری با اندازه n که در آن y_i مقدار پاسخ را برای مشاهده i ام نشان می‌دهد.

خط رگرسیون برای p ویژگی به صورت زیر نمایش داده می‌شود:

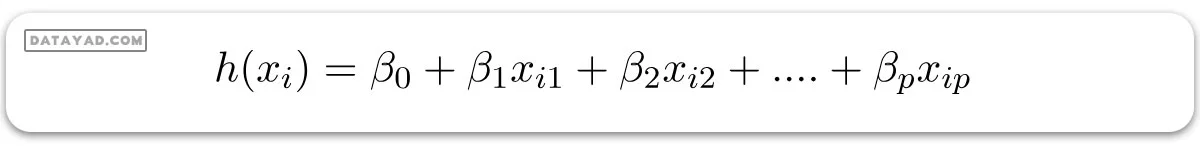
جایی که h(x_i) مقدار پاسخ پیش‌بینی شده برای مشاهده i ام و (ß , ß_{1 ,…,} ß_p) ضرایب رگرسیون هستند. همچنین، می‌توانیم بنویسیم:

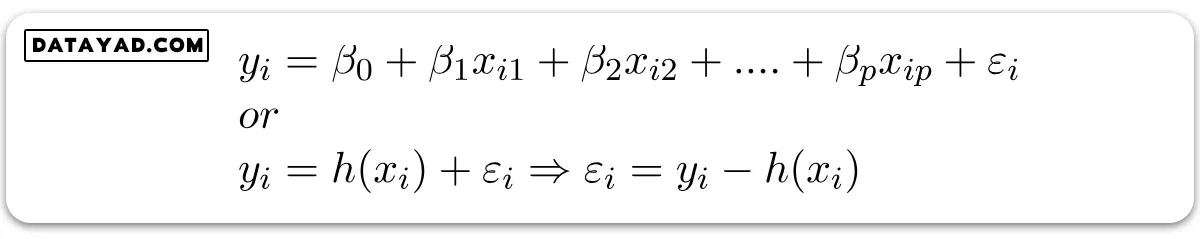
جایی که (ε_i) خطای باقی‌مانده در مشاهده i ام را نمایش می‌دهد. ما می‌توانیم مدل خطی خود را با نمایش ماتریس ویژگی X به صورت زیر، کمی بیشتر عمومیت بخشیم:

پس حالا، مدل خطی می‌تواند به شکل ماتریسی به این صورت بیان شود:

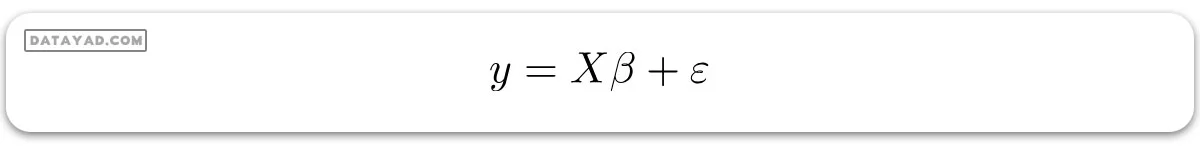
که:

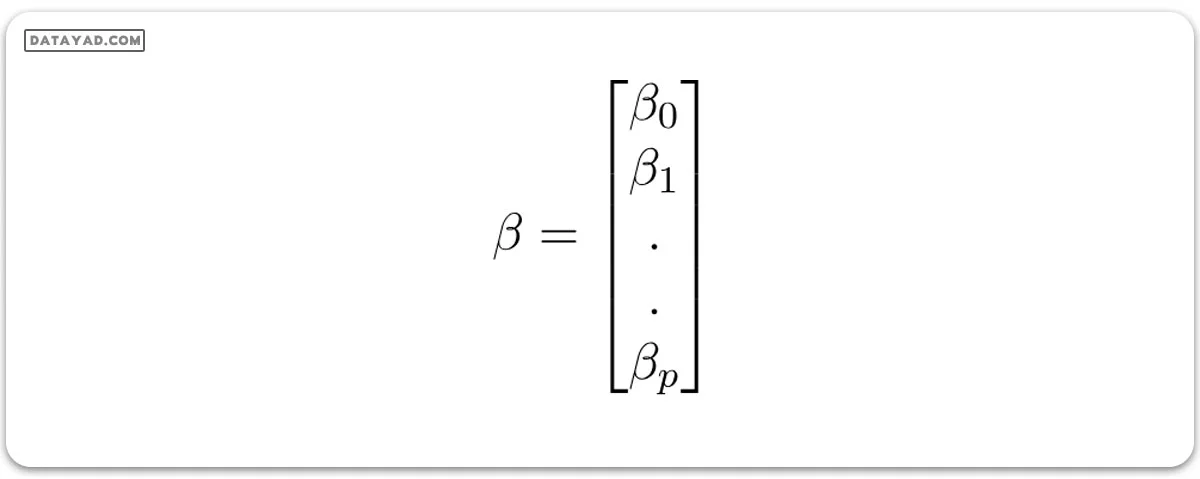
و:

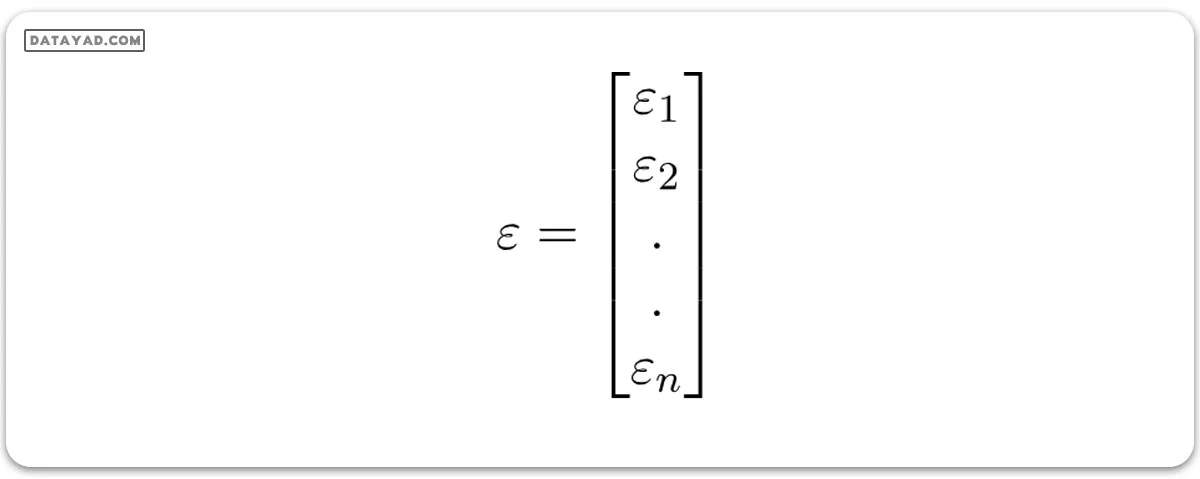
اکنون، ما یک برآورد از ß، یعنی (‘ß) را با استفاده از روش کمینه مربعات مشخص می‌کنیم. همانطور که قبلاً توضیح داده شد، روش کمینه مربعات سعی در تعیین (‘ß) دارد که برای آن خطای کل باقی‌مانده به حداقل می‌رسد.

ما نتیجه را مستقیماً در اینجا ارائه می‌دهیم:

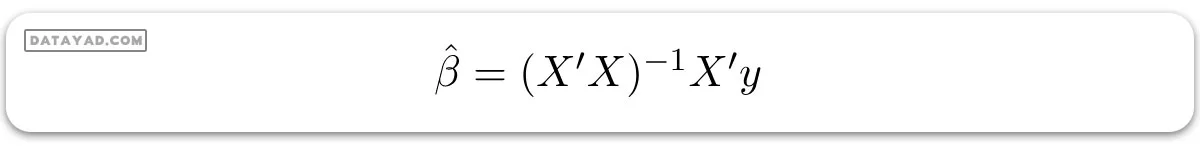
جایی که (‘) نشان‌دهنده ترانهاده ماتریس است در حالی که (1-) نشان‌دهنده معکوس ماتریس است. با دانستن تخمین‌های کمینه مربعات (‘ß)، حالا می‌توان مدل رگرسیون خطی چندگانه را به این شکل تخمین زد:

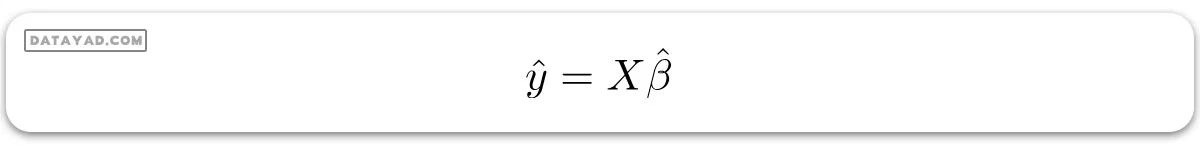
جایی که (‘y) بردار پاسخ تخمین زده شده است.

پیاده‌سازی پایتون برای تکنیک‌های رگرسیون خطی چندگانه

برای رگرسیون خطی چندگانه، ما از مجموعه داده‌های قیمت‌گذاری خانه‌های بوستون استفاده خواهیم کرد.

from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model, metrics

# load the boston dataset
data_url = "http://lib.stat.cmu.edu/datasets/boston"
raw_df = pd.read_csv(data_url, sep="\s+",
					skiprows=22, header=None)
X = np.hstack([raw_df.values[::2, :],
			raw_df.values[1::2, :2]])
y = raw_df.values[1::2, 2]

# splitting X and y into training and testing sets
X_train, X_test,\
	y_train, y_test = train_test_split(X, y,
									test_size=0.4,
									random_state=1)

# create linear regression object
reg = linear_model.LinearRegression()

# train the model using the training sets
reg.fit(X_train, y_train)

# regression coefficients
print('Coefficients: ', reg.coef_)

# variance score: 1 means perfect prediction
print('Variance score: {}'.format(reg.score(X_test, y_test)))

# plot for residual error

# setting plot style
plt.style.use('fivethirtyeight')

# plotting residual errors in training data
plt.scatter(reg.predict(X_train),
			reg.predict(X_train) - y_train,
			color="green", s=10,
			label='Train data')

# plotting residual errors in test data
plt.scatter(reg.predict(X_test),
			reg.predict(X_test) - y_test,
			color="blue", s=10,
			label='Test data')

# plotting line for zero residual error
plt.hlines(y=0, xmin=0, xmax=50, linewidth=2)

# plotting legend
plt.legend(loc='upper right')

# plot title
plt.title("Residual errors")

# method call for showing the plot
plt.show()

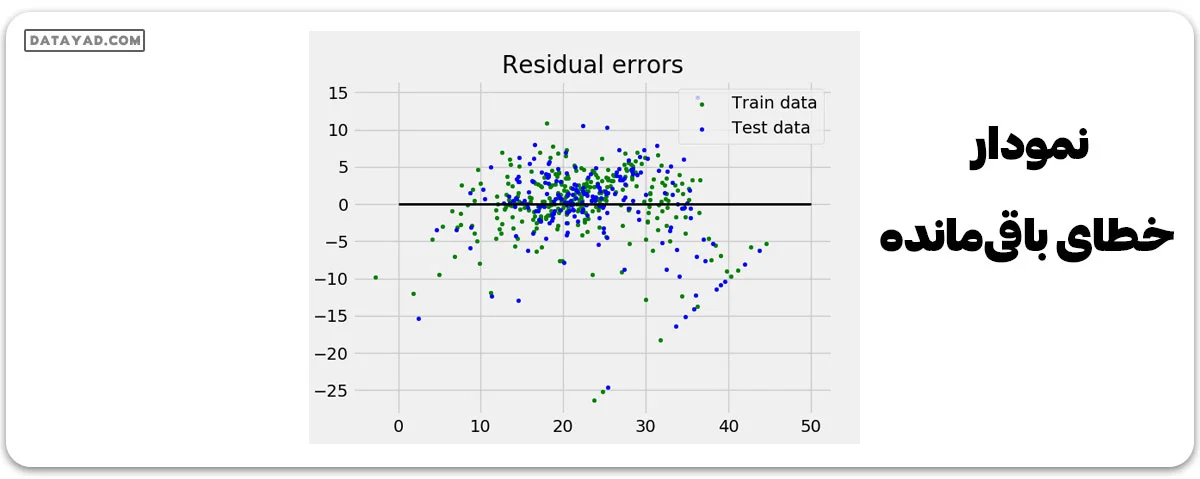
 خروجی:

Coefficients:
[ -8.80740828e-02   6.72507352e-02   5.10280463e-02   2.18879172e+00
-1.72283734e+01   3.62985243e+00   2.13933641e-03  -1.36531300e+00
2.88788067e-01  -1.22618657e-02  -8.36014969e-01   9.53058061e-03
-5.05036163e-01]
Variance score: 0.720898784611

و نمودار خطای باقی‌مانده به این شکل است:

در مثال بالا، ما مقدار دقت را با استفاده از نمره واریانس توضیح داده شده تعیین می‌کنیم.

تعریف می‌کنیم:

1 – Var{y – y’}/Var{y} = مقدار نمره واریانس توضیح داده شده

که در آن (‘y) خروجی هدف تخمین زده شده، ( y) خروجی هدف مرتبط (صحیح) و Var واریانس است، که مربع انحراف معیار است. بهترین دقت ممکن 1.0 است، مقادیر پایین‌تر کم دقت‌تر هستند.

فرض‌هایی که در مدل رگرسیون خطی در نظر می‌گیریم

در اینجا فرض‌های پایه‌ای آورده شده‌اند که مدل رگرسیون خطی درباره‌ی داده‌هایی که روی آنها اعمال می‌شود دارد:

✔️ رابطه خطی

بین پاسخ‌ها و ویژگی‌ها باید رابطه‌ای خطی وجود داشته باشد. این فرض با استفاده از نمودارهای پراکندگی قابل بررسی است. مثلاً، اولین شکل، متغیرهایی را نشان می‌دهد که رابطه‌ی خطی دارند، در حالی که متغیرهای شکل دوم و سوم احتمالاً غیر خطی هستند. پس، اولین شکل برای پیش‌بینی‌ها با استفاده از رگرسیون خطی مناسب‌تر است.

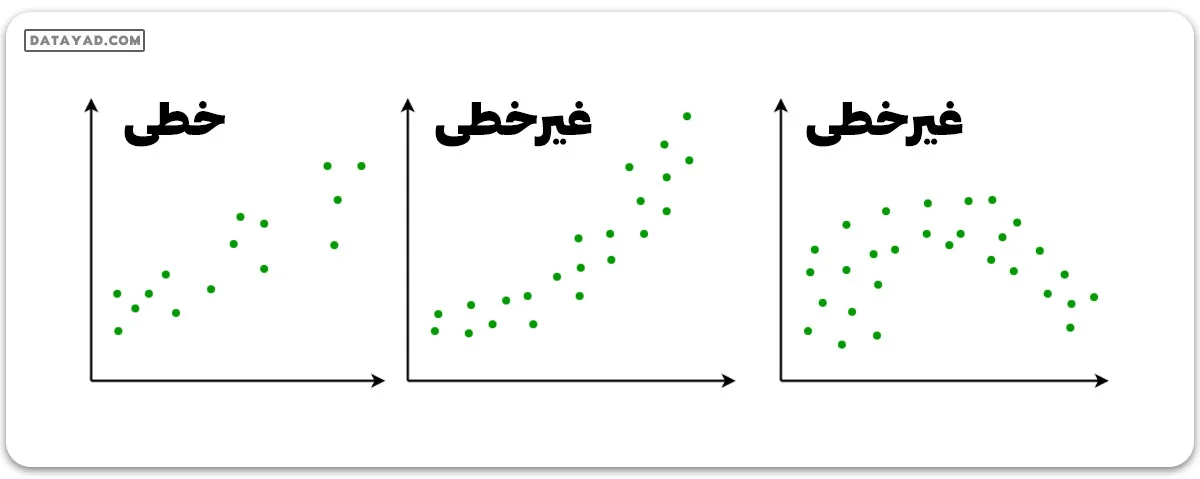
✔️ کم یا بدون هم‌خطی

فرض می‌شود که داده‌ها کمترین هم‌خطی را دارند یا اصلاً هم‌خطی ندارند. هم‌خطی زمانی رخ می‌دهد که ویژگی‌ها نسبت به هم مستقل نباشند.

✔️ کم یا بدون خودهمبستگی

فرض بر این است که در داده‌ها خودهمبستگی کمی وجود دارد یا اصلاً وجود ندارد. خودهمبستگی زمانی پیش می‌آید که خطاهای باقیمانده نسبت به هم مستقل نیستند.

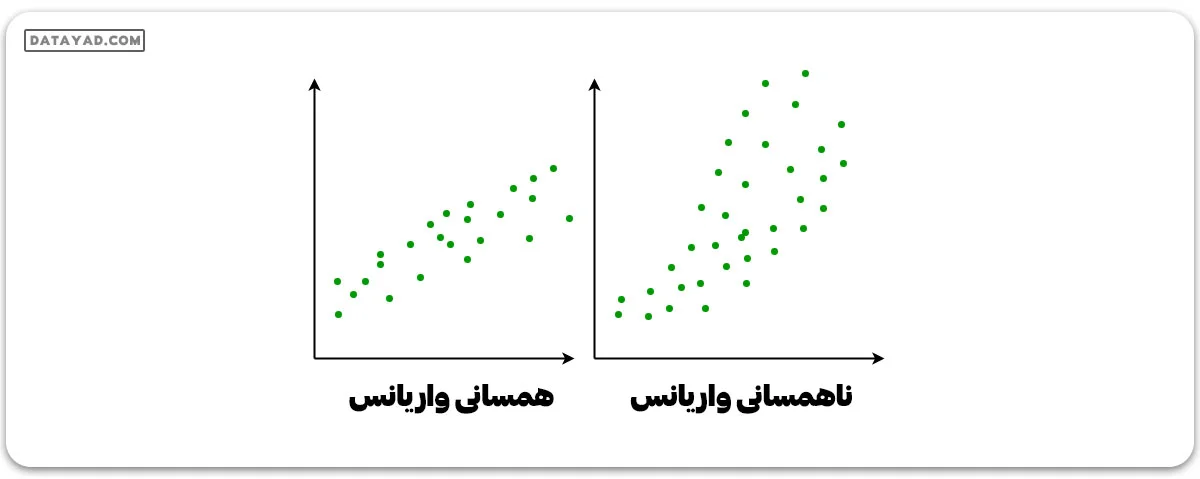
✔️ همسانی واریانس

این وضعیتی است که در آن ترم خطا – یا “نویز” یا برهم‌کنش تصادفی در رابطه بین متغیرهای مستقل و متغیر وابسته – برای تمام مقادیر متغیرهای مستقل یکسان است. مثلاً، شکل ۱ وضعیت همسانی واریانس را دارد، در حالی که شکل ۲ ناهمسانی واریانس را نشان می‌دهد.

همانطور که به پایان این مقاله پیاده سازی رگرسیون خطی در پایتون نزدیک می‌شویم، برخی از کاربردهای رگرسیون خطی را در زیر بحث می‌کنیم.

کاربردهای رگرسیون خطی

• خطوط روند: خطوط روند نشان‌دهنده تغییرات در داده‌های عددی با گذشت زمان هستند (مثل تولید ناخالص داخلی، قیمت نفت و غیره). این روندها معمولاً از الگویی خطی پیروی می‌کنند، بنابراین می‌توان از رگرسیون خطی برای پیش‌بینی مقادیر آتی استفاده کرد. با این وجود، این روش ممکن است در مواردی که تغییرات دیگری ممکن است داده‌ها را تحت تأثیر قرار دهند، دقت کمتری داشته باشد.
• اقتصاد: رگرسیون خطی یک ابزار تجربی اصلی در اقتصاد است. به عنوان مثال، برای پیش‌بینی مصرف کنندگان، هزینه‌های سرمایه‌ای ثابت، سرمایه‌گذاری در موجودی، خرید صادرات یک کشور، هزینه‌های واردات، تقاضای داشتن دارایی‌های نقدی، تقاضای کار و عرضه کار استفاده می‌شود.
• مالی: مدل قیمت‌گذاری دارایی‌های سرمایه از رگرسیون خطی برای تحلیل و سنجش ریسک‌های سیستماتیک یک سرمایه‌گذاری بهره می‌برد.
• زیست‌شناسی: رگرسیون خطی برای مدل‌سازی روابط علت و معلولی بین پارامترها در سیستم‌های بیولوژیک استفاده می‌شود.