گرادیان کاهشی (Gradient Descent) در پایتون: آموزش گام‌به‌گام + پیاده‌سازی عملی

بفرست برای دوستت

گرادیان کاهشی (Gradient Descent) یکی از پرکاربردترین و مهم‌ترین الگوریتم‌ها در دنیای یادگیری ماشین و هوش مصنوعی است. این الگوریتم به ما کمک می‌کند تا مدل‌های پیش‌بینی خود را بهینه کنیم و خطای پیش‌بینی را به حداقل برسانیم. اگر شما دانشجوی یادگیری ماشین، مهندس داده یا توسعه‌دهنده هوش مصنوعی هستید و می‌خواهید پیاده‌سازی گرادیان کاهشی در پایتون را یاد بگیرید، این مقاله گام‌به‌گام مخصوص شماست. . برای درک بهتر مفاهیم پایه، می‌توانید به مطلب یادگیری عمیق با پایتون مراجعه کنید.

در این راهنما، علاوه بر توضیح مفاهیم پایه، مثال‌های عملی و کدهای پایتون را مشاهده خواهید کرد تا بتوانید الگوریتم Gradient Descent را در پروژه‌های واقعی خود به کار ببرید. همچنین مطالعه تفاوت‌های هوش مصنوعی و یادگیری ماشین می‌تواند دید شما را نسبت به کاربرد گرادیان کاهشی گسترده‌تر کند.

گرادیان کاهشی چیست و چگونه کار می‌کند؟

گرادیان کاهشی (Gradient Descent) یک الگوریتم بهینه‌سازی عددی است که هدف آن پیدا کردن مقادیر پارامترهای مدل است تا تابع خطا (Loss Function) کمینه شود. به عبارت ساده‌تر، این الگوریتم کمک می‌کند مدل ما بهترین پیش‌بینی ممکن را داشته باشد.

یک تصویر شهودی از گرادیان کاهشی این است که تصور کنید در یک تپه مه‌آلود ایستاده‌اید و می‌خواهید به پایین‌ترین نقطه برسید، اما نمی‌توانید دور و بر را ببینید. راهکار شما این است که به سمت شیب نزولی زمین حرکت کنید. هر قدمی که برمی‌دارید، کمی به سمت پایین حرکت می‌کنید و با تکرار این روند، در نهایت به پایین‌ترین نقطه می‌رسید.

در یادگیری ماشین، پارامترهای مدل نقش موقعیت شما روی تپه را دارند و شیب تابع خطا نسبت به هر پارامتر نشان می‌دهد که کدام جهت شما را به کمینه تابع خطا نزدیک‌تر می‌کند. برای درک بهتر مفاهیم ریاضی و عملی، می‌توانید مقاله آموزش ریاضیات برای پایتون را مطالعه کنید.

نقش گرادیان کاهشی در آموزش مدل‌های یادگیری ماشین

محاسبه اختلاف بین پیش‌بینی مدل و داده واقعی.
به‌روزرسانی پارامترهای مدل در جهت کاهش خطا.
تکرار این روند تا زمانی که تغییرات بسیار کوچک شوند یا مدل به کمینه تابع خطا برسد.

با این توضیح، می‌توانیم به شکل عملی و ریاضی ببینیم چگونه گرادیان و نرخ یادگیری در این الگوریتم نقش دارند.

تعریف شهودی با مثال شیب‌نزولی (توضیح ریاضی ساده)

همان‌طور که قبلاً گفتیم، گرادیان کاهشی مانند پایین آمدن از یک تپه مه‌آلود است. اما در یادگیری ماشین، این «تپه» تابع خطا است و «شیب» گرادیان آن نسبت به پارامترهای مدل است.

توضیح ریاضی ساده

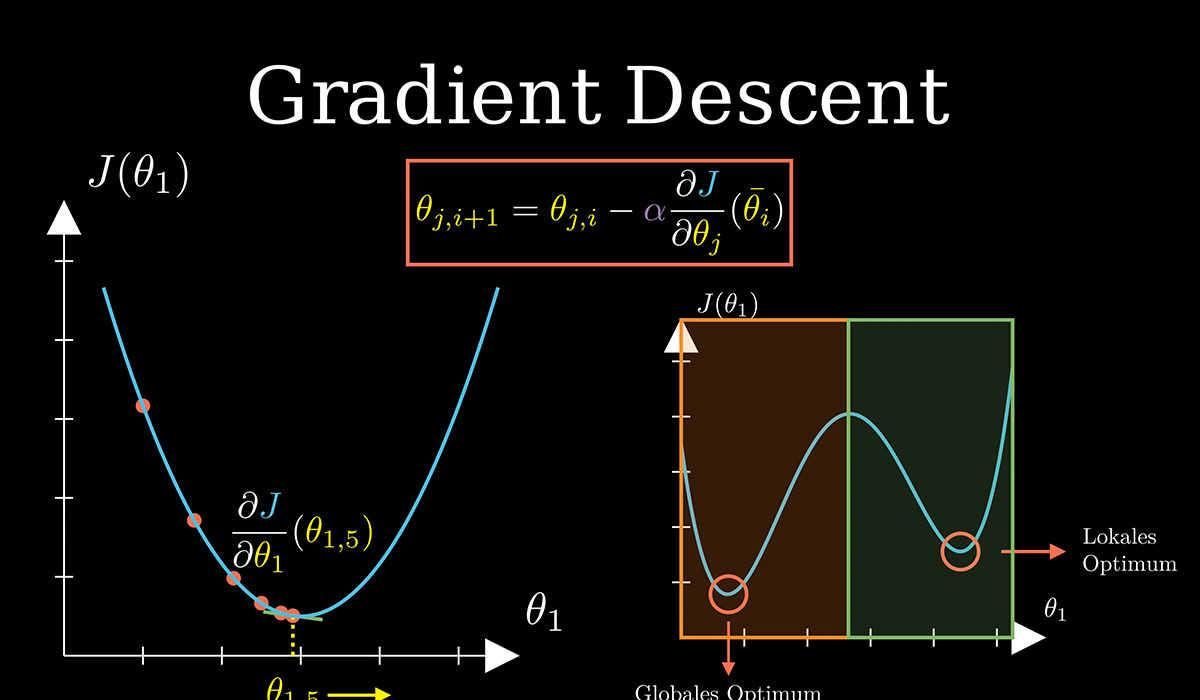
فرض کنید تابع خطا J(θ)J(\theta)J(θ) داریم که θ\thetaθ پارامتر مدل است. برای کمینه کردن JJJ، الگوریتم گرادیان کاهشی پارامترها را با فرمول زیر به‌روزرسانی می‌کند:

θ:=θ−α∂J(θ)∂θ\theta := \theta - \alpha \frac{\partial J(\theta)}{\partial \theta}θ:=θ−α∂θ∂J(θ)

که در آن:

α\alphaα نرخ یادگیری (Learning Rate) است و تعیین می‌کند هر قدم چقدر بزرگ باشد.
∂J(θ)∂θ\frac{\partial J(\theta)}{\partial \theta}∂θ∂J(θ) گرادیان تابع خطا نسبت به پارامتر θ\thetaθ است.

مثال ساده در پایتون

فرض کنید تابع خطای ما J(θ)=θ2J(\theta) = \theta^2J(θ)=θ2 باشد. گرادیان آن dJdθ=2θ\frac{dJ}{d\theta} = 2\thetadθdJ=2θ است. با الگوریتم گرادیان کاهشی، می‌توانیم θ\thetaθ را به سمت صفر حرکت دهیم:

# پیاده‌سازی ساده Gradient Descent

theta = 10  # مقدار اولیه

alpha = 0.1  # نرخ یادگیری

iterations = 50

for i in range(iterations):

    gradient = 2 * theta

    theta = theta - alpha * gradient

    print(f"Iteration {i+1}: theta = {theta}")

در این مثال، مشاهده می‌کنیم که مقدار $θ\theta$ θ به تدریج به صفر نزدیک می‌شود و تابع خطا کمینه می‌شود و می‌توان از روش‌هایی مشابه تحلیل داده با پایتون برای بررسی روند بهبود مدل و تصمیم‌گیری استفاده کرد.

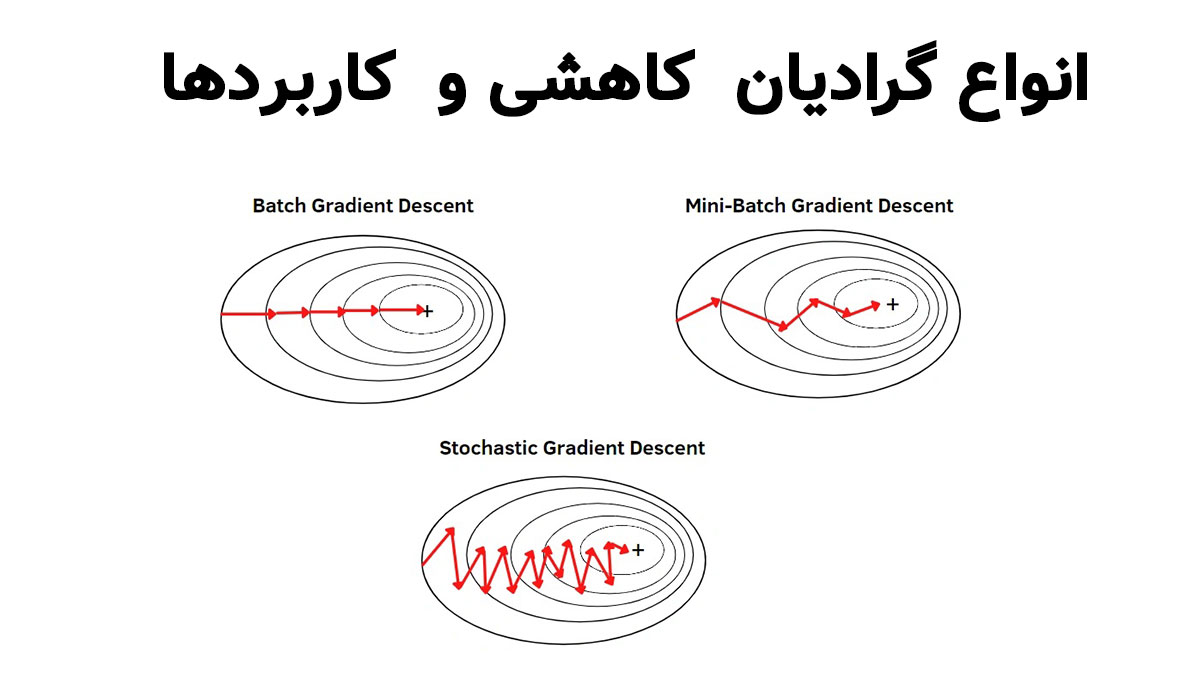
انواع گرادیان کاهشی و کاربردها

گرادیان کاهشی چند نوع دارد که هر کدام بسته به اندازه داده و سرعت آموزش، کاربرد خاص خود را دارند:

نوع گرادیان کاهشی	توضیح کوتاه	کاربرد اصلی	مزایا	معایب
گرادیان کاهشی دسته‌ای (Batch Gradient Descent)	کل داده‌ها برای محاسبه گرادیان استفاده می‌شود	داده‌های کوچک تا متوسط	بهینه‌ترین جهت کاهش خطا	زمان‌بر برای داده‌های بزرگ
گرادیان کاهشی تصادفی (Stochastic Gradient Descent – SGD)	یک نمونه داده در هر مرحله استفاده می‌شود	داده‌های بزرگ و آنلاین	سریع و مناسب برای داده‌های بزرگ	ممکن است به کمینه محلی نرسد و نوسان بیشتری دارد
گرادیان کاهشی مینی‌بچ (Mini-batch Gradient Descent)	ترکیبی از دسته‌ای و تصادفی، گروه‌های کوچک داده استفاده می‌شوند	یادگیری عمیق و شبکه‌های عصبی	تعادل بین سرعت و پایداری	نیاز به انتخاب اندازه مناسب مینی‌بچ
گرادیان کاهشی با شتاب (Momentum Gradient Descent)	اضافه کردن وزن به گرادیان‌های قبلی برای شتاب	شبکه‌های عمیق و توابع پیچیده	کاهش نوسانات و سرعت بیشتر	نیاز به تنظیم پارامتر شتاب
آدام (Adam Optimizer)	ترکیبی از Momentum و RMSProp	یادگیری عمیق و NLP	به طور خودکار نرخ یادگیری را تنظیم می‌کند	محاسبات پیچیده‌تر و حافظه بیشتر نیاز دارد

با استفاده از این جدول، دانشجویان و پژوهشگران می‌توانند به سرعت نوع گرادیان مناسب پروژه خود را انتخاب کنند و عملکرد مدل را بهینه کنند.

به نقل از سایت ibm:

« روش گرادیان نزولی دسته‌ای، خطا را برای هر نقطه در یک مجموعه آموزشی جمع می‌کند و مدل را تنها پس از ارزیابی تمام نمونه‌های آموزشی به‌روزرسانی می‌کند. این فرآیند به عنوان یک دوره آموزشی شناخته می‌شود.»

پیاده‌سازی گام به گام در پایتون

در این بخش، یک مثال ساده از گرادیان کاهشی برای کمینه کردن تابع خطا را با پایتون می‌بینیم. این مثال برای درک عملی الگوریتم بسیار مناسب است.

کد نمونه

فرض کنید تابع خطا $J(θ)=(θ−5)2J(\theta) = (\theta – 5)^2$ J(θ)=(θ−5)2 باشد و هدف پیدا کردن $θ=5\theta = 5$ θ=5 است:

# پیاده‌سازی Gradient Descent در پایتون

theta = 0  # مقدار اولیه

alpha = 0.1  # نرخ یادگیری

iterations = 50

for i in range(iterations):

    gradient = 2 * (theta - 5)

    theta = theta - alpha * gradient

    print(f"Iteration {i+1}: theta = {theta:.4f}")

 

print(f"Minimum found at theta = {theta:.4f}")

در این کد:

· gradient گرادیان تابع خطا است.

· theta با استفاده از نرخ یادگیری alpha به‌روزرسانی می‌شود.

· پس از چند تکرار، مقدار theta به 5 نزدیک می‌شود، یعنی کمینه تابع پیدا شده است.

تنظیم نرخ یادگیری (Learning Rate) بهینه

نرخ یادگیری $α\alpha$ α نقش بسیار مهمی در عملکرد گرادیان کاهشی دارد:

· اگر خیلی کوچک باشد: الگوریتم کند پیش می‌رود و نیاز به تکرارهای زیادی دارد.

· اگر خیلی بزرگ باشد: ممکن است الگوریتم از کمینه عبور کند و به جای همگرایی، نوسان داشته باشد.

· بهترین روش معمولاً شروع با یک مقدار کوچک و تنظیم آن بر اساس مشاهده روند کاهش تابع خطا است.

برای مثال:

alpha_values = [0.01, 0.1, 0.5]

for alpha in alpha_values:

    theta = 0

    for i in range(20):

        gradient = 2 * (theta - 5)

        theta = theta - alpha * gradient

    print(f"Alpha {alpha}: theta = {theta:.4f}")

با این روش می‌توان بهترین نرخ یادگیری را برای پروژه خود پیدا کرد.

بهینه‌سازی و چالش‌های رایج

گرادیان کاهشی ابزار قدرتمندی است، اما در عمل با چند چالش رایج روبه‌رو می‌شود. شناخت این چالش‌ها و راهکارهای آن‌ها باعث می‌شود مدل‌های دقیق‌تر و پایدارتر داشته باشیم.

چالش‌ها و نکات بهینه‌سازی

1. کمینه محلی (Local Minima):

o بعضی توابع پیچیده چند کمینه دارند. گرادیان کاهشی ممکن است در یک کمینه محلی گیر کند و به کمینه جهانی نرسد.

o راهکار: استفاده از نرخ یادگیری مناسب، الگوریتم‌هایی مانند Momentum یا Adam.

2. شیب‌های ناپایدار (Vanishing/Exploding Gradients):

o در شبکه‌های عصبی عمیق، گرادیان ممکن است بسیار کوچک یا بسیار بزرگ شود.

o راهکار: نرمال‌سازی داده‌ها، استفاده از توابع فعال‌سازی مناسب و الگوریتم‌های بهبود یافته.

3. انتخاب نرخ یادگیری:

o نرخ یادگیری بیش از حد کوچک کند است و بیش از حد بزرگ باعث نوسان یا واگرایی می‌شود.

o راهکار: امتحان چند مقدار، استفاده از نرخ یادگیری تطبیقی.

4. پردازش داده‌های بزرگ:

o گرادیان کاهشی دسته‌ای روی داده‌های بسیار بزرگ کند است.

o راهکار: استفاده از SGD یا Mini-batch Gradient Descent.

5. تنظیم پارامترهای الگوریتم:

o پارامترهایی مثل شتاب (Momentum)، نرخ یادگیری و اندازه مینی‌بچ باید به دقت انتخاب شوند تا الگوریتم عملکرد بهتری داشته باشد.

نکته عملی: ترکیب روش‌های بهینه‌سازی پیشرفته مثل Adam یا RMSProp باعث می‌شود هم سرعت آموزش بالا برود و هم مدل پایدارتر باشد.

جمع بندی

گرادیان کاهشی به‌عنوان یکی از ابزارهای اصلی بهینه‌سازی در یادگیری ماشین و هوش مصنوعی، نقش بسیار مهمی در کاهش خطای پیش‌بینی و بهبود عملکرد مدل‌ها دارد. با درک مفاهیم پایه این الگوریتم و پیاده‌سازی آن در پایتون، می‌توانیم روند یادگیری مدل‌ها را کنترل کرده و مدل‌های دقیق‌تر و کارآمدتری ایجاد کنیم. همچنین مطالعه دوره آموزش هوش مصنوعی از صفر به شما کمک می‌کند تا دید جامعی نسبت به کاربردهای گرادیان کاهشی و الگوریتم‌های پیشرفته‌تر داشته باشید.

در این مقاله، ابتدا با مفاهیم پایه و اصول گرادیان کاهشی آشنا شدیم، سپس با مثال‌های شهودی و گام‌به‌گام پیاده‌سازی آن، توانستیم کاربرد عملی این الگوریتم را مشاهده کنیم. مرور انواع گرادیان کاهشی و کاربرد هر نوع، کمک می‌کند تا با توجه به نیاز پروژه، بهترین نسخه الگوریتم را انتخاب کنیم و از نکات بهینه‌سازی آن در مسیر توسعه مدل‌های خود بهره‌مند شویم.

گام بعدی: می‌توانید با پیاده‌سازی گرادیان کاهشی روی مجموعه داده‌های واقعی، تجربه عملی کسب کنید و سپس با ترکیب آن با الگوریتم‌های پیشرفته‌تر مانند Adam یا RMSProp، به بهینه‌سازی سریع‌تر و دقیق‌تر مدل‌ها دست یابید.

سوالات متداول

1. آیا گرادیان کاهشی برای شبکه‌های عصبی عمیق کاربرد دارد؟

بله، گرادیان کاهشی و نسخه‌های بهبود یافته آن مثل SGD با Momentum و Adam پایه‌ای‌ترین الگوریتم‌ها برای آموزش شبکه‌های عصبی عمیق هستند.

2. نرخ یادگیری (Learning Rate) چگونه تعیین می‌شود؟

نرخ یادگیری معمولاً با آزمایش چند مقدار مختلف تعیین می‌شود. شروع با مقادیر کوچک و بررسی روند کاهش تابع خطا رایج است. استفاده از نرخ یادگیری تطبیقی نیز کمک زیادی می‌کند.

3. چه زمانی باید از Mini-batch Gradient Descent استفاده کنم؟

وقتی داده‌های شما بزرگ هستند و نمی‌خواهید حافظه زیادی مصرف کنید، یا می‌خواهید سرعت آموزش مناسب باشد، Mini-batch Gradient Descent بهترین انتخاب است.

4. گرادیان کاهشی همیشه به کمینه جهانی می‌رسد؟

نه، گرادیان کاهشی ممکن است در کمینه‌های محلی گیر کند، به خصوص در توابع پیچیده. برای کاهش این مشکل می‌توان از الگوریتم‌های پیشرفته مانند Adam یا RMSProp استفاده کرد.