یادگیری ماشین و هوش مصنوعی در سالهای اخیر به یکی از پرکاربردترین فناوریها در حوزههای مختلف تبدیل شدهاند. اما یکی از چالشهای اصلی در این زمینه، کار با دادههای حجیم و پربُعد است. هرچه تعداد ویژگیها یا متغیرهای یک مجموعه داده بیشتر باشد، پردازش و تحلیل آن سختتر میشود و مدلهای یادگیری ماشین نیز ممکن است با مشکلاتی مثل بیشبرازش (Overfitting)، افزایش زمان آموزش و کاهش دقت مواجه شوند.
اینجاست که تکنیکهای کاهش ابعاد (Dimensionality Reduction) وارد عمل میشوند. یکی از پرکاربردترین و مؤثرترین این روشها، تحلیل مؤلفههای اصلی یا PCA (Principal Component Analysis) است. این روش با استفاده از مفاهیم ریاضی و جبر خطی، ویژگیهای اصلی داده را استخراج کرده و ابعاد اضافی را حذف میکند؛ بدون آنکه اطلاعات کلیدی داده از بین برود.
PCA در یادگیری ماشین نهتنها به کاهش پیچیدگی دادهها کمک میکند، بلکه باعث افزایش سرعت الگوریتمها و حتی بهبود دقت مدلها در برخی شرایط میشود. از کاربردهای مهم آن میتوان به حذف نویز از دادههای زیستی، تحلیل دادههای مالی و حتی بهینهسازی شبکههای عصبی اشاره کرد.

PCA یا تحلیل مؤلفههای اصلی چیست؟
تحلیل مؤلفههای اصلی (Principal Component Analysis – PCA) یکی از مهمترین و پرکاربردترین روشهای کاهش ابعاد داده در یادگیری ماشین و دادهکاوی است. ایدهی اصلی PCA این است که دادههای چندبُعدی (که شامل ویژگیهای زیادی هستند) را به فضایی جدید منتقل کند که در آن، ویژگیها یا همان مؤلفههای اصلی (Principal Components) بیشترین میزان واریانس دادهها را توضیح دهند.
به زبان ساده، PCA به ما کمک میکند تا دادههای پیچیده را در ابعادی کمتر نمایش دهیم، بدون آنکه اطلاعات مهم آن از بین برود. این تکنیک نهتنها باعث صرفهجویی در زمان و منابع محاسباتی میشود، بلکه درک الگوها و روابط میان دادهها را نیز سادهتر میکند.
چرا PCA اهمیت دارد؟
- کاهش نویز دادهها: با حذف ویژگیهای کماهمیت، مدل روی اطلاعات ضروری تمرکز میکند.
- سرعت بیشتر: دادههای کمبعدی باعث میشوند الگوریتمهای یادگیری ماشین سریعتر آموزش ببینند.
- بهبود بصریسازی: در بسیاری از پروژهها، دادههای چندبعدی را نمیتوان بهسادگی ترسیم کرد. PCA کمک میکند دادهها را در 2 یا 3 بُعد نمایش دهیم.
- پیشگیری از بیشبرازش: مدلهایی که با دادههای کمبعد آموزش داده میشوند، کمتر درگیر پیچیدگیهای اضافی داده خواهند شد.
ارتباط PCA با جبر خطی
برای درک بهتر PCA باید کمی به مبانی جبر خطی برگردیم. زیرا این تکنیک بر اساس محاسبات ماتریسی و مفاهیم پایهای ریاضی عمل میکند.
- وکتورها و فضاهای برداری: هر ویژگی از داده را میتوان به صورت یک بردار در فضای چندبُعدی در نظر گرفت. وقتی دادهها چند ویژگی دارند، ما یک فضای n-بُعدی داریم.
- ماتریس کوواریانس: PCA به کمک ماتریس کوواریانس، میزان همبستگی میان ویژگیها را محاسبه میکند. اگر دو ویژگی همبستگی زیادی داشته باشند، PCA آنها را در یک مؤلفه ترکیب میکند.
- مقادیر و بردارهای ویژه (Eigenvalues و Eigenvectors): در قلب PCA، مفهومی به نام تجزیه مقادیر ویژه (Eigendecomposition) وجود دارد.
- بردار ویژه جهت مؤلفه اصلی را مشخص میکند.
- مقدار ویژه نشان میدهد هر مؤلفه چه مقدار از واریانس داده را توضیح میدهد.
- فضای جدید (Principal Components Space): دادهها از طریق ضرب ماتریسی روی این بردارهای ویژه نگاشته میشوند و در فضایی جدید با ابعاد کمتر نمایش داده میشوند.
بهطور خلاصه، PCA با استفاده از جبر خطی و محاسبات ماتریسی، ابعاد داده را کاهش داده و آنها را در جهاتی که بیشترین تغییرات داده رخ میدهد، نمایش میدهد.برای اینکه بتوانیم PCA را بهطور عملی اجرا کنیم، باید ابتدا با برخی از الگوریتمهای یادگیری ماشین آشنا باشیم که میتوانند با دادههای کاهش ابعاد یافته، کار کنند. این شناخت به ما کمک میکند تا انتخاب روش مناسب برای پیادهسازی و کاربرد PCA در پروژههای واقعی سادهتر شود.
برای تبدیل این دانش به مهارتهای کاربردی، پیشنهاد میکنیم از دورههای تخصصی یادگیری ماشین ما بازدید کنید.
قبل از ثبتنام، برای دریافت مشاوره رایگان با شماره ۰۹۹۰۵۵۰۱۹۹۸ تماس بگیرید
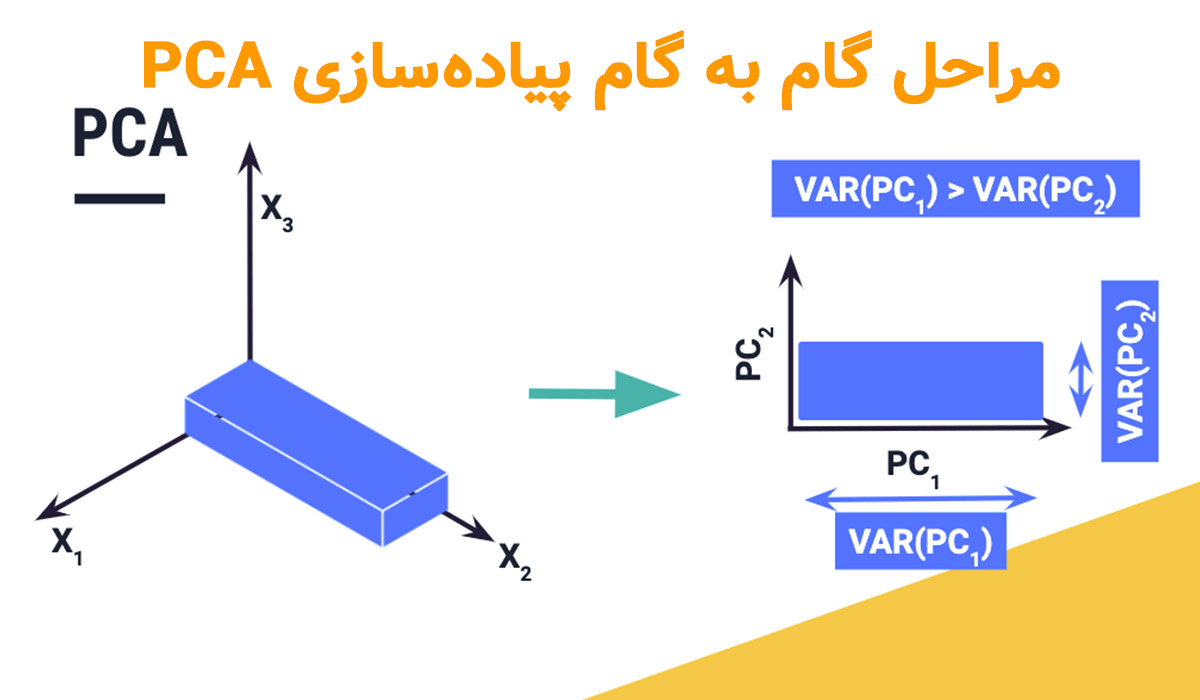
مراحل گام به گام پیادهسازی PCA
برای پیادهسازی PCA در یادگیری ماشین باید چند مرحلهی کلیدی طی شود. این مراحل از آمادهسازی دادهها شروع میشود و در نهایت به انتخاب مؤلفههای اصلی ختم میشود. هر مرحله اهمیت خاص خودش را دارد و اگر بهدرستی انجام نشود، نتیجهی نهایی معتبر نخواهد بود.
پیشپردازش دادهها (چرا Standardization ضروری است؟)
یکی از مهمترین مراحل قبل از اجرای PCA، استانداردسازی دادهها (Standardization) است.
دلیل اصلی این کار این است که ویژگیهای مختلف داده معمولاً مقیاسهای متفاوتی دارند. برای مثال:
- ویژگی «درآمد» ممکن است در مقیاس میلیونها تومان باشد.
- ویژگی «سن» در مقیاس دهههاست.
اگر این مقیاسها یکسانسازی نشوند، ویژگیهایی با دامنهی بزرگتر تأثیر بیشتری در محاسبات خواهند داشت و جهت مؤلفههای اصلی را منحرف میکنند.
در استانداردسازی، هر ویژگی بهگونهای تغییر میکند که میانگین آن ۰ و انحراف معیار آن ۱ باشد. این کار تضمین میکند که همه ویژگیها سهم مساوی در تحلیل داشته باشند.
محاسبه ماتریس کوواریانس و تجزیه آن
پس از استانداردسازی دادهها، باید بفهمیم که ویژگیها چطور با یکدیگر در ارتباطاند. اینجاست که ماتریس کوواریانس وارد عمل میشود.
- ماتریس کوواریانس نشان میدهد دو ویژگی چقدر با یکدیگر همبستگی دارند.
- اگر کوواریانس مثبت باشد، یعنی افزایش یکی معمولاً باعث افزایش دیگری میشود.
- اگر منفی باشد، یعنی افزایش یکی باعث کاهش دیگری میشود.
- اگر نزدیک به صفر باشد، یعنی دو ویژگی مستقل از یکدیگرند.
گام بعدی، محاسبه مقادیر ویژه (Eigenvalues) و بردارهای ویژه (Eigenvectors) از این ماتریس است.
- بردارهای ویژه جهت مؤلفههای اصلی را مشخص میکنند.
- مقادیر ویژه بیان میکنند که هر مؤلفه چه میزان واریانس دادهها را توضیح میدهد.
انتخاب مولفههای اصلی (نمودار Scree Plot)
همهی مؤلفههای اصلی اهمیت یکسانی ندارند. بنابراین باید تصمیم بگیریم که چند مؤلفه را انتخاب کنیم.
یکی از ابزارهای رایج در این مرحله، نمودار Scree Plot است.
- در این نمودار، مقادیر ویژه روی محور عمودی و تعداد مؤلفهها روی محور افقی نمایش داده میشوند.
- معمولاً یک «نقطه زانو» (Elbow Point) در نمودار وجود دارد که پس از آن، مقادیر ویژه کاهش چشمگیری پیدا میکنند.
- مؤلفههایی که قبل از این نقطه قرار دارند، بیشترین اطلاعات را در خود دارند و برای تحلیل انتخاب میشوند.
در عمل، بسته به پروژه، ممکن است تنها ۲ یا ۳ مؤلفه کافی باشند؛ مخصوصاً وقتی هدف، بصریسازی دادههاست.
به نقل از سایت geeksforgeeks:
«PCA معمولاً برای پیشپردازش دادهها برای استفاده با الگوریتمهای یادگیری ماشین استفاده میشود. این تکنیک به حذف افزونگی، بهبود کارایی محاسباتی و آسانتر کردن تجسم و تجزیه و تحلیل دادهها، به ویژه هنگام کار با دادههای با ابعاد بالا، کمک میکند.»
مقایسه PCA با سایر روشهای کاهش ابعاد
کاهش ابعاد (Dimensionality Reduction) فقط محدود به PCA نیست. روشهای متنوعی وجود دارند که هرکدام بر اساس منطق و الگوریتم خاص خود عمل میکنند. انتخاب روش مناسب بستگی به نوع داده، هدف پروژه و منابع محاسباتی دارد. در جدول زیر، PCA را با چند روش مهم دیگر مثل LDA، t-SNE و Autoencoder مقایسه میکنیم:
جدول مقایسهای روشهای کاهش ابعاد
| روش کاهش ابعاد | مزایا | معایب | کاربردها |
| PCA (تحلیل مؤلفههای اصلی) | – ساده و سریع- مبتنی بر جبر خطی- حفظ بیشترین واریانس داده | – خطی بودن (در دادههای غیرخطی عملکرد ضعیف دارد)- تفسیر مؤلفهها دشوار است | – پردازش تصویر با پایتون- فشردهسازی داده- حذف نویز از دادهها |
| LDA (تحلیل تفکیکی خطی) | – تمرکز بر جداسازی کلاسها- مناسب برای دادههای برچسبدار | – فقط برای مسائل طبقهبندی کاربرد دارد- نیازمند برچسبهای دقیق | – تشخیص چهره- مسائل طبقهبندی متنی و صوتی |
| t-SNE (t-Distributed Stochastic Neighbor Embedding) | – مناسب برای دادههای غیرخطی- حفظ ساختار محلی دادهها | – بسیار کند برای دادههای بزرگ- فقط برای مصورسازی (Visualization) مؤثر است | – نمایش دادههای پیچیده در 2D یا 3D- تحلیل دادههای ژنتیکی |
| Autoencoder (خودرمزگذار) | – توانایی مدلسازی روابط غیرخطی- انعطافپذیر در دادههای پیچیده | – نیاز به دادهی زیاد و منابع محاسباتی بالا- آموزش سختتر از PCA | – یادگیری عمیق- کاهش ابعاد تصاویر- فشردهسازی در شبکههای عصبی |
همانطور که مشاهده میکنید، PCA هنوز یکی از بهترین انتخابها برای پروژههایی است که نیاز به سرعت، سادگی و تفسیرپذیری نسبی دارند. اما در پروژههای پیچیدهتر مثل دادههای غیرخطی یا شبکههای عصبی عمیق، روشهایی مانند t-SNE و Autoencoder گزینههای بهتری هستند.
کاربردهای PCA در پروژههای واقعی
یکی از دلایل محبوبیت PCA در یادگیری ماشین این است که فقط یک مفهوم تئوری نیست، بلکه در پروژههای عملی و حوزههای مختلف کاربردهای گستردهای دارد.همچنین یکی از کاربردهای مهم PCA، آموزش رایگان یادگیری ماشین با پایتون است. با استفاده از این روش، دانشجویان و مهندسان میتوانند مفاهیم کاهش ابعاد و استخراج مؤلفههای اصلی را روی دادههای واقعی تمرین کنند و درک عملی بهتری از پروژههای پردازش تصویر، تحلیل دادههای ژنتیکی و بهینهسازی مدلهای یادگیری عمیق پیدا کنند. در ادامه، سه مورد از مهمترین کاربردهای آن را بررسی میکنیم:
کاهش ابعاد در پردازش تصویر (MNIST Dataset)
تصاویر معمولاً شامل هزاران یا حتی میلیونها پیکسل هستند. بهعنوان مثال، دیتاست معروف MNIST شامل تصاویر دستنوشتهی اعداد (۰ تا ۹) با ابعاد 28×28 پیکسل است. این یعنی هر تصویر 784 ویژگی (پیکسل) دارد.
- اگر بخواهیم مدل یادگیری ماشین روی این دادهها آموزش دهیم، حجم محاسبات بسیار زیاد خواهد شد.
- PCA کمک میکند این 784 ویژگی را به مثلاً 50 یا حتی 30 مؤلفه اصلی کاهش دهیم، بدون اینکه اطلاعات مهم تصویر از بین برود.
- نتیجه: سرعت بیشتر در آموزش مدل و کاهش خطر بیشبرازش.
حذف نویز از دادههای ژنتیکی
یکی دیگر از کاربردهای PCA در علوم زیستی و پزشکی است. دادههای ژنتیکی معمولاً شامل هزاران ویژگی (ژنها) هستند که بسیاری از آنها دارای نویز یا دادههای تکراریاند.
- PCA میتواند ویژگیهای غیرمهم و پرنویز را حذف کند و فقط ترکیبهای اصلی ژنها را نگه دارد.
- این کار باعث میشود محققان بتوانند الگوهای اصلی در دادههای ژنتیکی را بهتر شناسایی کنند.
- بهطور مثال، در تحقیقات سرطان یا بیماریهای ارثی، استفاده از PCA کمک میکند عوامل اصلی بیماریها راحتتر کشف شوند.
بهینهسازی مدلهای یادگیری عمیق
شبکههای عصبی عمیق (Deep Learning) معمولاً برای آموزش به دادههای عظیم و پربُعد نیاز دارند. این موضوع باعث افزایش زمان آموزش و نیاز به منابع سختافزاری سنگین میشود.
- با استفاده از PCA، میتوان ابعاد ورودی دادهها را کاهش داد.
- نتیجه این است که مدل سریعتر آموزش میبیند و حافظهی کمتری مصرف میشود.
- همچنین PCA در انتخاب ویژگیهای مؤثر کمک میکند، بهویژه وقتی دادهها شامل ویژگیهای غیرضروری زیادی باشند.

اشتباهات رایج در استفاده از PCA
هرچند PCA در یادگیری ماشین یک ابزار قدرتمند برای کاهش ابعاد داده است، اما استفادهی نادرست از آن میتواند نتایج مدل را بهشدت تحت تأثیر قرار دهد. در ادامه، به رایجترین خطاهایی که متخصصان داده در هنگام استفاده از PCA مرتکب میشوند اشاره میکنیم:
۱. نادیده گرفتن استانداردسازی دادهها
بزرگترین اشتباه این است که دادهها را قبل از اجرای PCA استانداردسازی (Standardization) نکنیم.
- اگر ویژگیها مقیاسهای متفاوتی داشته باشند، ویژگیهایی با دامنهی بزرگتر بر مؤلفههای اصلی غالب میشوند.
- نتیجه: جهت مؤلفهها به اشتباه تعیین میشود و مدل به اطلاعات غلط متکی خواهد بود.
۲. انتخاب تعداد نامناسب مؤلفهها
بعضی افراد یا خیلی کم مؤلفه انتخاب میکنند (و اطلاعات مهم از دست میرود) یا بیش از حد مؤلفه نگه میدارند (و عملاً کاهش ابعاد فایدهای ندارد).
- بهترین روش، استفاده از نمودار Scree Plot یا نسبت واریانس تجمعی (Cumulative Variance Ratio) است.
- معمولاً نگهداشتن مؤلفههایی که مجموعاً ۸۰ تا ۹۰ درصد واریانس را توضیح میدهند کافی است.
۳. استفاده از PCA برای دادههای غیرخطی
PCA ذاتاً یک روش خطی است. بنابراین وقتی دادهها دارای روابط غیرخطی باشند (مثل دادههای پیچیدهی تصویری یا ژنتیکی)، نتایج ممکن است رضایتبخش نباشند.
- در چنین شرایطی روشهایی مثل Kernel PCA یا t-SNE عملکرد بهتری خواهند داشت.
۴. تفسیر اشتباه مؤلفهها
گاهی کاربران تصور میکنند که مؤلفههای اصلی همان ویژگیهای اولیه هستند. در حالیکه PCA ترکیبی خطی از ویژگیهای اصلی میسازد.
- بنابراین تفسیر مستقیم آنها دشوار است.
- این موضوع بهویژه در پروژههایی مثل پزشکی یا علوم اجتماعی اهمیت دارد، چون تفسیرپذیری دادهها حیاتی است.
۵. اعمال PCA بدون بررسی هدف پروژه
گاهی صرفاً به دلیل اینکه PCA یک روش معروف است، روی دادهها اعمال میشود. اما:
- در پروژههایی که تفسیر ویژگیها مهمتر از سرعت یا کاهش ابعاد است، استفاده از PCA توصیه نمیشود.
- مثلاً در پروژههای تحلیل دادههای مالی، ممکن است از دست رفتن تفسیرپذیری ویژگیها آسیبزننده باشد.
نتیجه اینکه: PCA ابزاری بسیار ارزشمند است، اما تنها زمانی باید از آن استفاده کرد که هدف پروژه، کاهش پیچیدگی دادهها یا حذف نویز باشد و تفسیر مستقیم ویژگیها اولویت نداشته باشد.در نهایت، برای کسانی که میخواهند مسیر خود را در دنیای هوش مصنوعی و یادگیری ماشین به شکل حرفهای ادامه دهند، درک مفاهیم PCA و سایر تکنیکهای کاهش ابعاد یک مهارت کلیدی محسوب میشود.
پیادهسازی PCA در پایتون (کد عملی)
یکی از مزیتهای بزرگ PCA اینه که هم در کتابخانههای معروف پایتون مثل scikit-learn بهراحتی پیادهسازی شده و هم میتونیم مرحلهبهمرحله خودمون محاسباتش رو انجام بدیم. در اینجا یک مثال عملی با دیتاست معروف Iris رو بررسی میکنیم:
مرحله ۱: وارد کردن کتابخانهها و دیتاست
import numpy as np import matplotlib.pyplot as plt from sklearn import datasets from sklearn.preprocessing import StandardScaler from sklearn.decomposition import PCA # بارگذاری دیتاست Iris iris = datasets.load_iris() X = iris.data y = iris.target
مرحله ۲: استانداردسازی دادهها
# استانداردسازی (میانگین=0 و واریانس=1) scaler = StandardScaler() X_std = scaler.fit_transform(X)
مرحله ۳: اعمال PCA
# اجرای PCA و کاهش ابعاد به 2 مولفه اصلی
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_std)
print("واریانس توضیح داده شده هر مؤلفه:", pca.explained_variance_ratio_)
مرحله ۴: مصورسازی نتایج
plt.figure(figsize=(8,6))
for target, color in zip([0,1,2], ['r', 'g', 'b']):
plt.scatter(X_pca[y == target, 0],
X_pca[y == target, 1],
label=iris.target_names[target],
c=color)
plt.xlabel("مولفه اصلی 1")
plt.ylabel("مولفه اصلی 2")
plt.legend()
plt.title("نمایش دادههای Iris پس از کاهش ابعاد با PCA")
plt.show()
خروجی این کد:
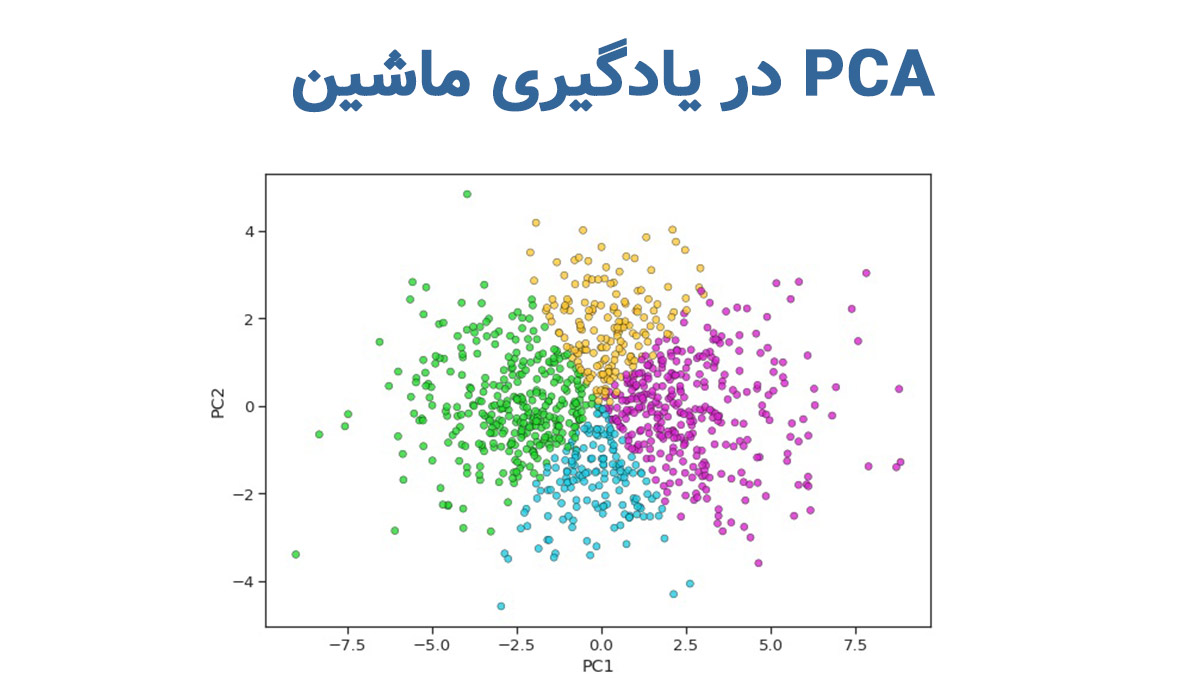
- دادههای Iris (که در ابتدا ۴ ویژگی داشتند) به ۲ مؤلفه اصلی کاهش مییابند.
- با ترسیم نمودار، میبینیم که سه کلاس مختلف گلها (Setosa، Versicolor و Virginica) در یک فضای دوبُعدی از هم جدا میشوند.
این مثال ساده نشون میده که PCA میتونه دادههای چندبُعدی رو فشرده کنه و همچنان الگوهای اصلی رو حفظ کنه.
در پروژههای بزرگتر مثل پردازش تصویر با پایتون یا تحلیل داده با پایتون همین مراحل روی دیتاستهای بسیار پیچیدهتر اجرا میشن.
جمع بندی
PCA در یادگیری ماشین یکی از بنیادیترین و در عین حال پرکاربردترین روشهای کاهش ابعاد است که نقش مهمی در تحلیل دادههای پیچیده و حجیم ایفا میکند. این روش با استفاده از مفاهیم جبر خطی، دادهها را از فضای اولیه به فضایی جدید منتقل کرده و مؤلفههایی را استخراج میکند که بیشترین واریانس را در دادهها توضیح میدهند.
اربردهای PCA بسیار متنوعاند؛ از پردازش تصویر با پایتون (مثل دیتاست MNIST) گرفته تا حذف نویز از دادههای ژنتیکی و بهینهسازی مدلهای یادگیری عمیق. این نشان میدهد که PCA فقط یک ابزار تئوری نیست، بلکه در پروژههای واقعی میتواند سرعت محاسبات را افزایش دهد، از بیشبرازش جلوگیری کند و حتی دقت مدلها را بهبود بخشد.
البته باید به محدودیتها و اشتباهات رایج هم توجه داشت. PCA یک روش خطی است و برای دادههای غیرخطی ممکن است بهترین گزینه نباشد. همچنین انتخاب تعداد نامناسب مؤلفهها یا نادیده گرفتن مرحلهی استانداردسازی میتواند کل نتایج را بیاعتبار کند.
در نهایت، اگر بهدنبال روشی سریع، ساده و مؤثر برای کاهش ابعاد دادهها هستید، PCA یک انتخاب ایدهآل خواهد بود. اما همیشه به یاد داشته باشید که انتخاب روش کاهش ابعاد باید متناسب با نوع داده و هدف پروژه باشد.
برای تبدیل این دانش به مهارتهای کاربردی، پیشنهاد میکنیم از دورههای تخصصی یادگیری ماشین ما بازدید کنید.
قبل از ثبتنام، برای دریافت مشاوره رایگان با شماره ۰۹۹۰۵۵۰۱۹۹۸ تماس بگیرید
سوالات متداول
۱. چه زمانی از تحلیل مؤلفههای اصلی (PCA) بهجای دیگر تکنیکهای کاهش ابعاد استفاده کنیم؟
وقتی هدف اصلی کاهش ابعاد داده و افزایش سرعت محاسبات باشد و در عین حال ساختار کلی دادهها حفظ شود، استفاده از PCA بهترین گزینه است.
- برای پروژههایی مثل پردازش تصویر، تحلیل دادههای مالی یا دادههای ژنتیکی، PCA انتخاب بسیار خوبی است.
- اگر نیاز به مدلسازی غیرخطی داشته باشیم، باید سراغ روشهایی مثل Kernel PCA یا t-SNE برویم.
۲. در چه مواردی استفاده از PCA ممکن است نتایج نامطلوبی داشته باشد؟
- وقتی دادهها غیرخطی باشند و PCA نتواند روابط پیچیده را مدل کند.
- در پروژههایی که تفسیر ویژگیها اهمیت بالایی دارد (مثل پزشکی یا تحلیلهای اجتماعی). چون مؤلفههای اصلی ترکیبی از ویژگیها هستند و تفسیر مستقیمشان سخت است.
- وقتی دادهها بهخوبی استانداردسازی نشده باشند، نتایج PCA میتواند کاملاً گمراهکننده باشد.
۳. آیا PCA میتواند دقت مدلهای یادگیری ماشین را بهبود دهد؟
بله، در بسیاری از موارد.
- حذف ویژگیهای غیرضروری باعث میشود مدل روی دادههای اصلیتر تمرکز کند.
- این موضوع باعث کاهش بیشبرازش (Overfitting) میشود.
- همچنین زمان آموزش مدل بهشدت کاهش مییابد.
۴. تفاوت PCA با LDA چیست؟
- PCA یک روش غیرنظارتی (Unsupervised) است و به برچسب دادهها نیازی ندارد.
- LDA یک روش نظارتی (Supervised) است که با استفاده از برچسبها سعی میکند کلاسها را از هم جدا کند.
- بنابراین PCA بیشتر برای کاهش ابعاد کلی بهکار میرود، در حالی که LDA برای بهبود طبقهبندی استفاده میشود.
۵. آیا میتوان PCA را همراه با الگوریتمهای یادگیری عمیق استفاده کرد؟
بله، در بسیاری از پروژهها قبل از تغذیه دادهها به شبکههای عصبی، ابتدا با PCA ابعاد داده کاهش مییابد. این کار باعث سرعت بیشتر آموزش و استفاده بهینه از منابع سختافزاری میشود.















