رگرسیون چندجمله‌ای برای داده‌ های غیرخطی

در درس ۳۰ ام از آموزش رایگان یادگیری ماشین با پایتون در سایت دیتایاد می خواهیم به رگرسیون چندجمله‌ای برای داده‌ های غیرخطی بپردازیم.

معمولاً در زندگی روزمره با داده‌های غیرخطی (Non-linear data) روبه‌رو هستیم. برخی از معادلات حرکت که در فیزیک مطالعه می‌شوند را در نظر بگیرید:

✔️ حرکت پرتابی: ارتفاع یک پرتابه با استفاده از معادله h = -½ gt² + ut + ho محاسبه می‌شود.

✔️ معادله حرکت در سقوط آزاد: فاصله‌ای که یک جسم پس از سقوط آزاد تحت جاذبه برای ‘t’ ثانیه طی می‌کند، با gt² ½ محاسبه می‌شود.

✔️ فاصله طی شده توسط یک جسم با شتاب یکنواخت: فاصله می‌تواند به صورت ut + ½at2 محاسبه شود

که در آن،

• g = شتاب ناشی از جاذبه
• u = سرعت اولیه
• ho = ارتفاع اولیه
• a = شتاب

علاوه بر این مثال‌ها، روندهای غیرخطی نیز در نرخ رشد بافت‌ها، پیشرفت بیماری‌های همه‌گیر، تابش جسم سیاه، حرکت آونگ و غیره مشاهده می‌شوند. این مثال‌ها به وضوح نشان می‌دهند که ما همیشه نمی‌توانیم یک رابطه خطی بین ویژگی‌های مستقل و وابسته داشته باشیم. بنابراین، رگرسیون خطی انتخاب ضعیفی برای مقابله با چنین شرایط غیرخطی است. اینجاست که رگرسیون چندجمله‌ ای به کمک ما می‌آید!!

رگرسیون چندجمله‌ای یک تکنیک قدرتمند برای مواجهه با شرایطی است که در آن رابطه غیرخطی از درجه دوم، سوم یا بالاتر وجود دارد. مفهوم اساسی در رگرسیون چندجمله‌ای این است که توان‌های هر ویژگی مستقل به عنوان ویژگی‌های جدید اضافه شده و سپس یک مدل خطی بر این مجموعه گسترش یافته از ویژگی‌ها آموزش داده می‌شود. بیایید با یک مثال استفاده از رگرسیون چندجمله‌ای را نشان دهیم. شرایطی را در نظر بگیرید که در آن متغیر وابسته y نسبت به یک متغیر مستقل x با رابطه زیر تغییر می‌کند:

y = 13x² + 2x + 7

ما برای پیاده‌سازی از کلاس PolynomialFeatures در کتابخانه Scikit-Learn استفاده خواهیم کرد.

مرحله 1: کتابخانه‌ها را وارد کرده و یک مجموعه داده تصادفی تولید کنید. 

# Importing the libraries 
import numpy as np 
import matplotlib.pyplot as plt 
from sklearn.linear_model import LinearRegression 
from sklearn.preprocessing import PolynomialFeatures 
from sklearn.metrics import mean_squared_error, r2_score 

# Importing the dataset 
## x = data, y = quadratic equation 
x = np.array(7 * np.random.rand(100, 1) - 3) 
x1 = x.reshape(-1, 1) 
y = 13 * x*x + 2 * x + 7

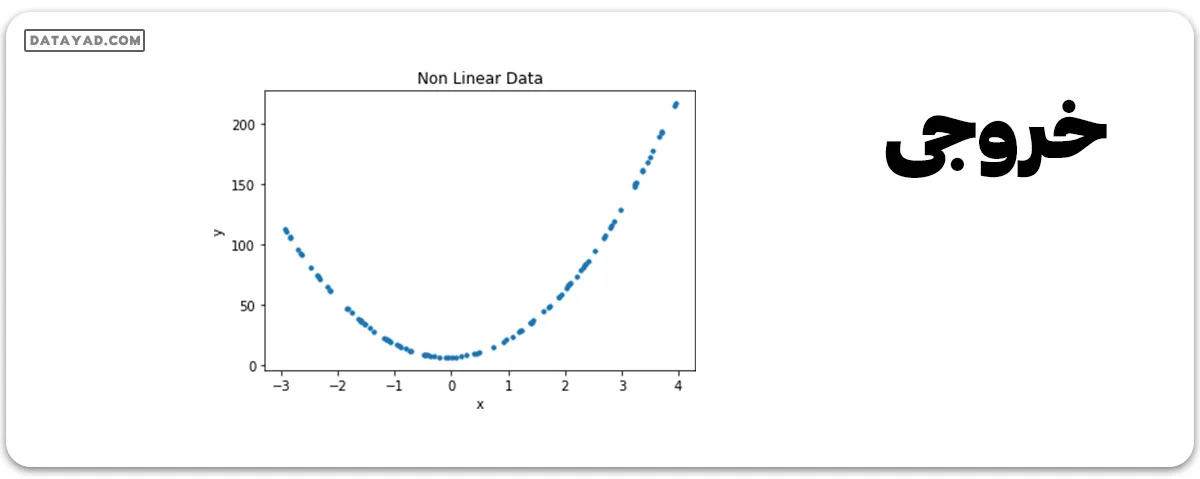
مرحله 2: نقاط داده را رسم کنید. 

# data points 
plt.scatter(x, y, s = 10) 
plt.xlabel('x') 
plt.ylabel('y') 
plt.title('Non Linear Data') 

مرحله 3: ابتدا سعی کنید داده‌ها را با استفاده از مدل خطی منطبق کنید. 

# Model initialization 
regression_model = LinearRegression() 
# Fit the data(train the model) 
regression_model.fit(x1, y) 
print('Slope of the line is', regression_model.coef_) 
print('Intercept value is', regression_model.intercept_) 
# Predict 
y_predicted = regression_model.predict(x1) 

 خروجی:

Slope of the line is [[14.87780012]]
Intercept value is [58.31165769]

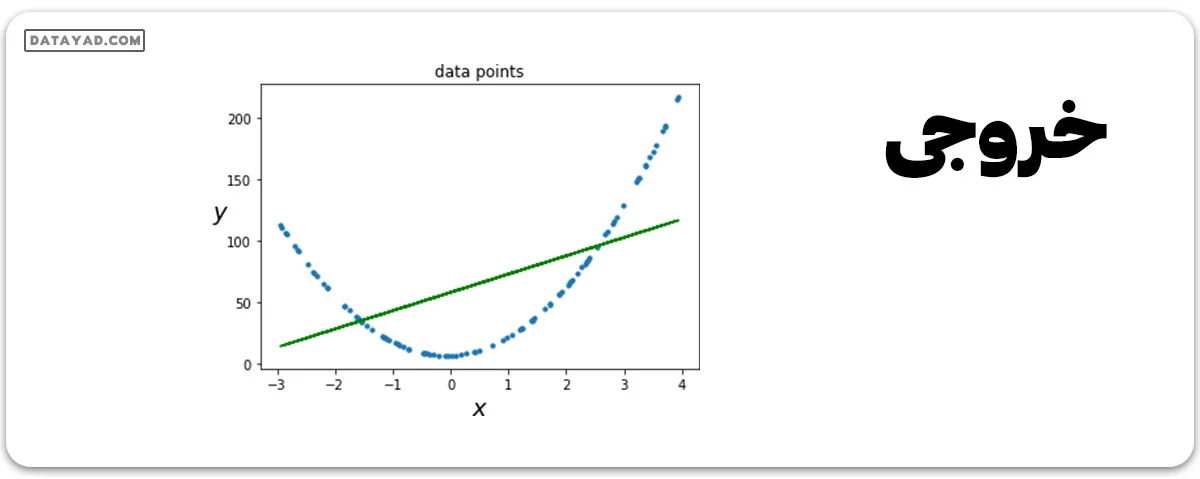
مرحله 4: نقاط داده و منحنی خطی را رسم کنید. 

# data points 
plt.scatter(x, y, s = 10) 
plt.xlabel("$x$", fontsize = 18) 
plt.ylabel("$y$", rotation = 0, fontsize = 18) 
plt.title("data points") 

# predicted values 
plt.plot(x, y_predicted, color ='g') 

Equation of the linear model is y = 14.87x + 58.31

مرحله 5: کارایی مدل را بر اساس خطای مربع میانگین، خطای مجذور میانگین مربعات و امتیاز r2 محاسبه کنید. 

# model evaluation 
mse = mean_squared_error(y, y_predicted) 

rmse = np.sqrt(mean_squared_error(y, y_predicted)) 
r2 = r2_score(y, y_predicted) 

# printing values 

print('MSE of Linear model', mse) 

print('R2 score of Linear model: ', r2) 

 خروجی:

MSE of Linear model 2144.8229656677095
R2 score of Linear model:  0.3019970606151057

عملکرد مدل خطی خوب نیست. حالا بیایید رگرسیون چندجمله‌ای درجه 2 را امتحان کنیم.

مرحله 6: برای بهبود عملکرد، باید مدل را پیچیده‌تر کنیم. پس، یک چندجمله‌ای درجه 2 را منطبق کرده و سپس رگرسیون خطی انجام دهیم. 

poly_features = PolynomialFeatures(degree = 2, include_bias = False) 
x_poly = poly_features.fit_transform(x1) 
x[3] 

 خروجی:

Out[]:array([-2.84314447])

علاوه بر ستون x، یک ستون دیگر هم اضافه شده که مربع داده‌های اصلی است. حالا با رگرسیون خطی ساده ادامه می‌دهیم. 

lin_reg = LinearRegression() 
lin_reg.fit(x_poly, y) 
print('Coefficients of x are', lin_reg.coef_) 
print('Intercept is', lin_reg.intercept_) 

 خروجی:

Coefficients of x are [[ 2. 13.]]
Intercept is [7.]

معادله دلخواه ما به این شکل است:

13x² + 2x + 7

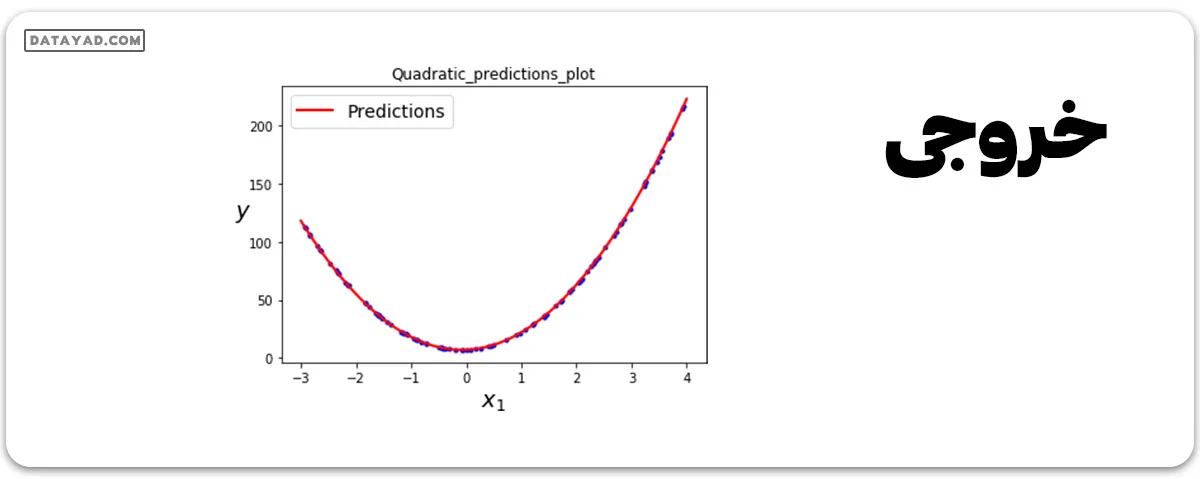
مرحله 7: معادله درجه دوی به دست آمده را رسم کنید. 

x_new = np.linspace(-3, 4, 100).reshape(100, 1) 
x_new_poly = poly_features.transform(x_new) 
y_new = lin_reg.predict(x_new_poly) 
plt.plot(x, y, "b.") 
plt.plot(x_new, y_new, "r-", linewidth = 2, label ="Predictions") 
plt.xlabel("$x_1$", fontsize = 18) 
plt.ylabel("$y$", rotation = 0, fontsize = 18) 
plt.legend(loc ="upper left", fontsize = 14) 

plt.title("Quadratic_predictions_plot") 
plt.show() 

مرحله 8: عملکرد مدل به دست آمده از رگرسیون چندجمله‌ای را محاسبه کنید.

y_deg2 = lin_reg.predict(x_poly) 
# model evaluation 
mse_deg2 = mean_squared_error(y, y_deg2) 

r2_deg2 = r2_score(y, y_deg2) 

# printing values 

print('MSE of Polyregression model', mse_deg2) 

print('R2 score of Linear model: ', r2_deg2) 

 خروجی:

MSE of Polyregression model 7.668437973562934e-28
R2 score of Linear model:  1.0

عملکرد مدل رگرسیون چندجمله‌ای برای معادله درجه دو داده شده، بسیار بهتر از مدل رگرسیون خطی است.

نکات مهم: PolynomialFeatures (درجه = d) یک آرایه حاوی n ویژگی را به یک آرایه حاوی:

(n + d)! / d! 

ویژگی، تبدیل می کند.

نتیجه‌گیری: رگرسیون چندجمله‌ای یک روش مؤثر برای مقابله با داده‌های غیرخطی است زیرا می‌تواند روابط بین ویژگی‌ها را که مدل رگرسیون خطی ساده در یافتن آنها دچار مشکل می‌شود، بیابد.