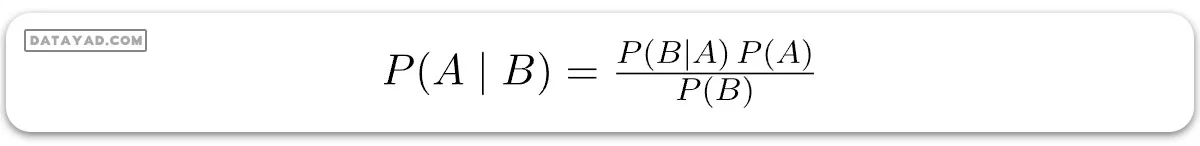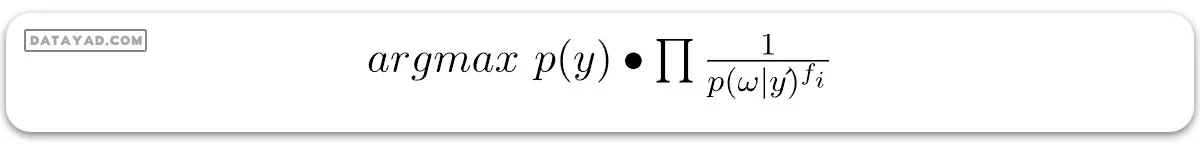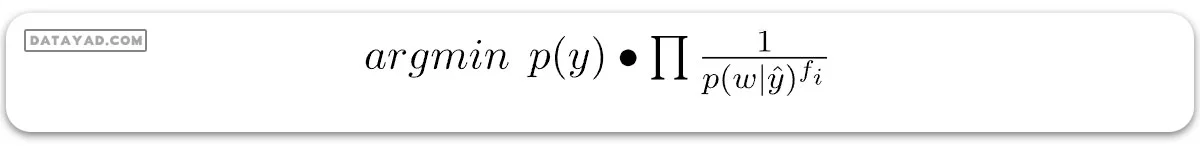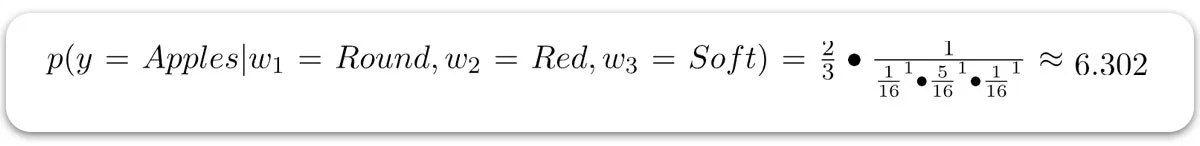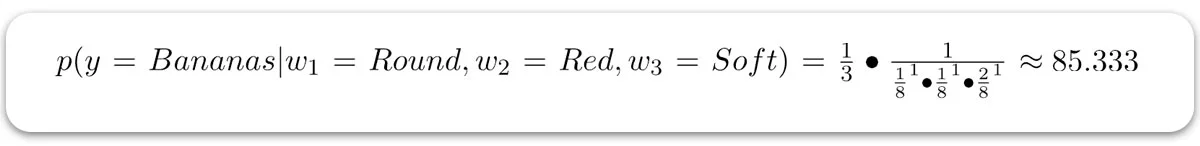الگوریتمهای بیز ساده (Naive Bayes algorithms) گروهی از الگوریتمهای یادگیری ماشین پرطرفدار و کاربردی در زمینه طبقهبندی هستند. روشهای مختلفی برای پیادهسازی الگوریتم بیز ساده وجود دارد، مثل بیز ساده گوسی، بیز ساده چندجملهای و غیره.
بیز ساده مکمل (Complement Naive Bayes) نوعی سازگاری از الگوریتم بیز ساده چندجملهای استاندارد است. بیز ساده چندجملهای در مجموعههای داده نامتوازن عملکرد خوبی ندارد. مجموعههای داده نامتوازن آنهایی هستند که تعداد نمونههای یک کلاس بیشتر از دیگر کلاسها است. این بدین معنی است که توزیع نمونهها یکسان نیست. کار کردن با این نوع دادهها میتواند سخت باشد چرا که مدل ممکن است به راحتی به دادهها بیشبرازش کند، به خصوص به کلاسی که تعداد نمونههای بیشتری دارد.
نحوه عملکرد CNB
بیز ساده مکمل به خصوص برای کار با مجموعههای داده نامتوازن مناسب است. در بیز ساده مکمل، به جای محاسبه احتمال تعلق یک آیتم به یک کلاس خاص، احتمال تعلق آیتم به تمام کلاسها محاسبه میشود. این مفهوم کلمه «مکمل» است و به همین دلیل به آن بیز ساده مکمل گفته میشود.
توضیح ساده و گام به گام الگوریتم (بدون استفاده از محاسبات پیچیده)
– برای هر کلاس، احتمال اینکه نمونه داده شده به آن تعلق نداشته باشد را حساب کنید.
– پس از انجام محاسبه برای همه کلاسها، همه مقادیر حساب شده را بررسی کرده و کوچکترین مقدار را انتخاب کنید.
– کوچکترین مقدار (پایینترین احتمال) انتخاب میشود چون این پایینترین احتمال است که آن نمونه متعلق به آن کلاس خاص نیست. این به معنای داشتن بیشترین احتمال برای واقعاً تعلق داشتن به آن کلاس است. پس این کلاس انتخاب میشود.
توجه: ما کلاس با بالاترین مقدار را انتخاب نمیکنیم چون ما در حال محاسبه مکمل احتمال هستیم. کلاسی که بالاترین مقدار را دارد، کمترین احتمال را دارد که نمونه متعلق به آن باشد.
حالا یک مثال را در نظر بگیریم:
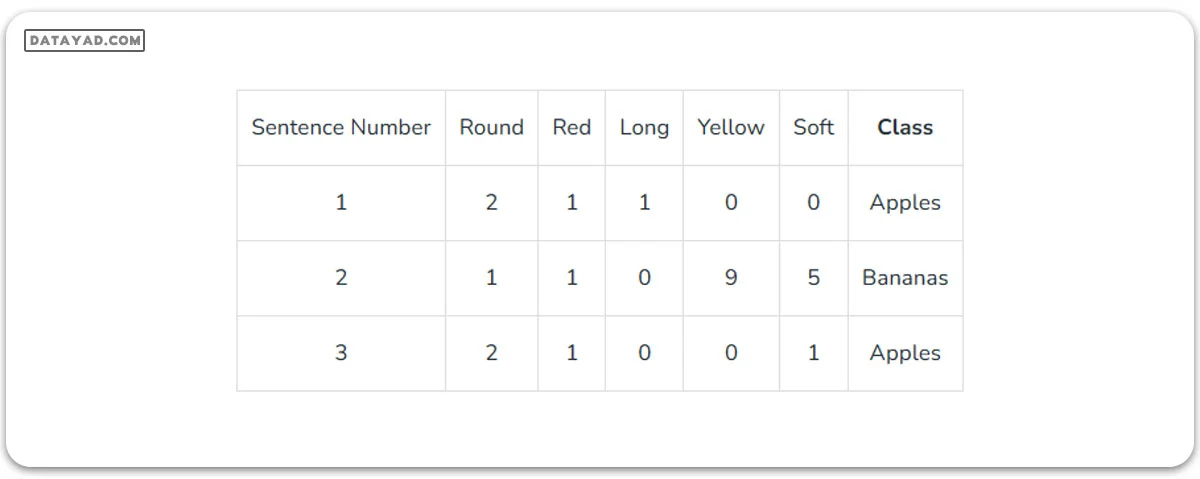
فرض کنید ما دو کلاس داریم: سیبها و موزها و باید تشخیص دهیم که آیا یک جمله داده شده مربوط به سیبها یا موزها است، بر اساس فراوانی تعداد مشخصی از کلمات. در اینجا یک نمایش جدولی از مجموعه داده ساده وجود دارد.
تعداد کل کلمات در کلاس «سیبها»:
(2+1+1) + (2+1+1) = 8
تعداد کل کلمات در کلاس «موزها»:
(1 + 1 + 9 + 5) = 16
بنابراین، احتمال اینکه یک جمله به کلاس «سیبها» تعلق داشته باشد:
به همین ترتیب، احتمال اینکه یک جمله به کلاس «موزها» تعلق داشته باشد:
در جدول بالا، دادهها به گونهای نمایش داده شدهاند که ستونها فراوانی کلمات در یک جمله مشخص را نشان میدهند و سپس نشان میدهند که جمله به کدام کلاس تعلق دارد. قبل از شروع، ابتدا باید با قضیه بیز آشنا شوید. قضیه بیز برای یافتن احتمال وقوع یک رویداد، با توجه به اینکه رویداد دیگری رخ داده است، استفاده میشود. فرمول آن به صورت زیر است:
که در آن A و B رویدادها هستند، P(A) احتمال وقوع A است، و P(A|B) احتمال وقوع A با فرض اینکه رویداد B قبلاً رخ داده است. P(B)، احتمال وقوع رویداد B نمیتواند 0 باشد چون قبلاً رخ داده است.
حال بیایید ببینیم که بیز ساده و بیز ساده مکمل چگونه کار میکنند. فرمول الگوریتم بیز ساده معمولی به صورت زیر است:
که در آن fi فراوانی برخی ویژگیها است. به عنوان مثال، تعداد دفعاتی که کلمات خاصی در یک جمله رخ میدهند.
اما در بیز ساده مکمل، فرمول به این شکل است:
اگر دقیقتر به فرمولها نگاه کنید، میبینید که بیز ساده مکمل فقط معکوس بیز ساده معمولی است. در بیز ساده، کلاسی که بیشترین مقدار را از فرمول به دست میآورد، کلاس پیشبینی شده است. بنابراین، چون بیز ساده مکمل فقط معکوس است، کلاسی که کمترین مقدار را از فرمول CNB به دست میآورد، کلاس پیشبینی شده است.
حال بیایید یک مثال را با استفاده از مجموعه دادههایمان و الگوریتم CNB تحلیل کنیم.
ما باید مقادیر زیر را محاسبه کنیم:
و
ما باید هر دو مقدار را مقایسه کنیم و کلاس با کمترین مقدار را به عنوان کلاس پیشبینی شده انتخاب کنیم. اگر مقدار برای (y = سیبها) کمتر باشد، کلاس پیشبینی شده سیبها خواهد بود، و اگر مقدار برای (y = موزها) کمتر باشد، کلاس پیشبینی شده موزها خواهد بود.
با استفاده از فرمول CNB برای هر دو کلاس، داریم:
چون 6.302 < 85.333 است، پس کلاس پیشبینی شده سیبها خواهد بود.
ما کلاس با مقدار بالاتر را انتخاب نمیکنیم چون مقدار بالاتر نشان میدهد که احتمال کمتری وجود دارد که یک جمله با آن کلمات متعلق به آن کلاس باشد. همین دلیل است که این الگوریتم بیز ساده مکمل نامیده میشود.
چه زمانی از CNB استفاده کنیم؟
– وقتی دادهها نامتوازن هستند: اگر مجموعه دادهای که قرار است روی آن طبقهبندی انجام شود نامتوازن باشد، بیز ساده چندجملهای و بیز ساده گوسی ممکن است دقت پایینی داشته باشند. اما بیز ساده مکمل عملکرد خوبی خواهد داشت و دقت نسبتاً بالاتری را ارائه میدهد.
– برای وظایف طبقهبندی متن: بیز ساده مکمل در وظایف طبقهبندی متن، هم از بیز ساده گوسی و هم از بیز ساده چندجملهای بهتر عمل میکند.
پیادهسازی CNB در پایتون
برای این مثال، از مجموعه داده شراب استفاده میکنیم که کمی نامتوازن است. این مجموعه داده مبدأ شراب را از روی پارامترهای شیمیایی مختلف تعیین میکند.
برای ارزیابی مدل، دقت مجموعه داده آزمایشی و گزارش طبقهبندی کلاسیفایر (طبقهبندی کننده یا دستهبند) را بررسی خواهیم کرد. ما از کتابخانه scikit-learn برای پیادهسازی الگوریتم بیز ساده مکمل استفاده خواهیم برد.
# Import required modules
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, classification_report
from sklearn.naive_bayes import ComplementNB
# Loading the dataset
dataset = load_wine()
X = dataset.data
y = dataset.target
# Splitting the data into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.15, random_state = 42)
# Creating and training the Complement Naive Bayes Classifier
classifier = ComplementNB()
classifier.fit(X_train, y_train)
# Evaluating the classifier
prediction = classifier.predict(X_test)
prediction_train = classifier.predict(X_train)
print(f"Training Set Accuracy : {accuracy_score(y_train, prediction_train) * 100} %\n")
print(f"Test Set Accuracy : {accuracy_score(y_test, prediction) * 100} % \n\n")
print(f"Classifier Report : \n\n {classification_report(y_test, prediction)}")
خروجی:
Training Set Accuracy : 65.56291390728477 %
Test Set Accuracy : 66.66666666666666 %
Classifier Report :
precision recall f1-score support
0 0.64 1.00 0.78 9
1 0.67 0.73 0.70 11
2 1.00 0.14 0.25 7
accuracy 0.67 27
macro avg 0.77 0.62 0.58 27
weighted avg 0.75 0.67 0.61 27
ما روی مجموعه دادههای آموزشی دقت 65.56٪ و روی مجموعه دادههای آزمایشی دقت 66.66٪ به دست آوردیم. این دقتها تقریباً مشابه هستند و با توجه به کیفیت مجموعه دادهها، واقعاً خوب محسوب میشوند. این مجموعه دادهها به خاطر سختی در طبقهبندی با دستهبندهای ساده مانند آنچه که ما استفاده کردیم، شناخته شدهاند. پس این دقتها قابل قبول هستند.
نتیجهگیری
حالا که با دستهبندهای بیز ساده مکمل و نحوه کار آنها آشنا شدید، دفعه بعد که با مجموعه دادههای نامتوازن روبرو شدید، میتوانید از بیز ساده مکمل استفاده کنید.
منابع: